На плоскости даны точки А(-5; -6), В(11; 6), С(0; 6). Выполним чертеж треугольника:
а) длину стороны ВС найдем как длину вектора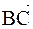 
:
.
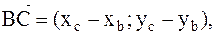
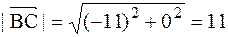Уравнение стороны ВС можно найти как уравнение прямой, проходящей через две точки:
В нашем случае
ВС: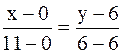 
,
или 
- каноническое уравнение.
Замечание. Форма записи канонического уравнения является условной и в ней не деление на ноль, а отношение. Такую запись следует читать следующим образом: х так относится к единице, как (y-6) относится к нулю.
Из полученного канонического уравнения выведем все остальные уравнения:
- параметрические уравнения;
- общее уравнение;
- уравнение с угловым коэффициентом, k=0 - угловой коэффициент.
Так как коэффициент перед переменной х в общем уравнении равен 0, то уравнения в отрезках для данной прямой не существует.
б) косинус угла А найдем как косинус угла между векторами 
и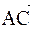 
.
Находим 
т.к.
то в нашем случае
в) уравнение искомой прямой можно найти как уравнение прямой, проходящей через заданную точку 
, параллельно заданному вектору 
:
.
В нашем случае
или 
г) длину высоты к стороне ВС можно найти как расстояние от точки А до прямой ВС. Для этого общее уравнение прямой ВС приведем к нормальному уравнению.
Т.к. 
- нормальный вектор прямой ВС, 
то при делении общего уравнения прямой на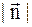 
получаем - нормальное уравнение прямой ВС. Чтобы найти расстояние от точки до прямой надо координаты этой точки подставить в нормальное уравнение прямой, а затем найти модуль полученного числа. В нашем случае получаем
.
Уравнение высоты к стороне ВС можно найти как уравнение прямой, проходящей через заданную точку 
перпендикулярно заданному нормальному вектору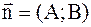 
:
.
Искомая высота проходит через точку А(-5; -6) и имеет нормальный вектор 
т.е. уравнение высоты
.
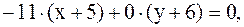
д) найдем основание медианы М - середину стороны ВС:
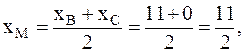
т.е.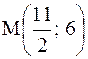 
.
Уравнение медианы АМ можно найти как уравнение прямой, проходящей через две заданные точки А и М:
.
В нашем случае
АМ: 
, 
.
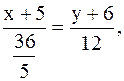
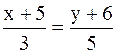е) как известно, центр описанной окружности лежит на пересечении серединных перпендикуляров. Т.о. к двум сторонам надо построить серединные перпендикуляры и найти точку их пересечения - центр описанной около треугольника окружности.
Середина стороны ВС есть точка 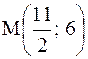, вектор 
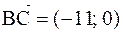- нормальный вектор серединного перпендикуляра к стороне ВС, т.е. уравнение серединного перпендикуляра имеет вид
Аналогично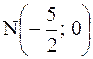 
- середины стороны АС, 
- нормальный вектор серединного перпендикуляра к АС и его уравнение имеет вид
Найдем точку пересечения серединных перпендикуляров, т.е. решим систему
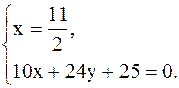
Откуда 
, т.о. 
- центр описанной около треугольника АВС окружности.
Чтобы найти радиус R описанной окружности, достаточно найти расстояние от центра до любой из вершин треугольника. Например, рассмотрим точки О и А, тогда
, 
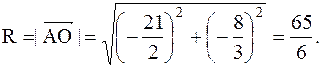
ж) в пункте г) уже была найдена длина высоты h к стороне ВС, тогда площадь треугольника АВС можно найти как полупроизведение основания ВС и высоты h, т.е. 
з) как известно, центр тяжести H треугольника лежит на пересечении его медиан. Но можно сделать более простым способом, а именно, как среднее арифметическое соответствующих координат вершин треугольника, т.е.
Получили Н(2, 2) - центр тяжести треугольника.
