Алгебра и аналитическая геометрия. Математический анализ
Индивидуальные задания и методические указания
для студентов ФДПО ИНО специальности 220100
Вычислительные машины, комплексы, системы и сети
Содержание
Введение………………………………………………………………… …….4
1. Индивидуальные задания по алгебре и аналитической геометрии.……..5
1.1. Задание 1………………………………………………………………..5
1.2. Задание 2 …………………………………………….. ………………..7
1.3. Задание 3………………………………………………………………..9
1.4. Задание 4 …………………………………………….………………..12
1.5. Задание 5………………………………………………………………14
2. Указания к решению заданий по алгебре и аналитической
геометрии…………………………………………………………………..15
2.1. Пример выполнения задания 1……………………………………….15
2.2. Пример выполнения задания 2……………………………………….20
2.3. Пример выполнения задания 4……………………………………….22
2.4. Пример выполнения задания 5……………………………………….27
3. Индивидуальные задания по математическому анализу……….……..33
3.1. Задание 1………………………………………………………………33
3.2. Задание 2 …………………………………………….. ………………39
3.3. Задание 3………………………………………………………………41
3.4. Задание 4 …………………………………………….…………….….46
3.5. Задание 5………………………………………………………………49
3.6. Задание 6………………………………………………………………50
4. Указания к выполнению заданий по математическому анализу………55
4.1. Указания к заданию 1…………..……………………………………55
4.1.1. Основные теоретические положения…………………………55
4.1.2. Пример выполнения задания 1………………………………..57
4.2. Указания к заданию 2……..…………………………………………61
4.2.1. Основные теоретические положения…………………………61
4.2.2. Пример выполнения задания 2………………………………..62
4.3. Указания к заданиям 3 и 4……..…………………………………….64
4.3.1. Основные теоретические положения…………………………64
4.3.2. Пример выполнения задания 3………………………………..66
4.3.3. Пример выполнения задания 4………………………………..67
4.4. Указания к заданию 5……..……………………………………….. 68
4.4.1. Основные теоретические положения…………………………68
4.4.2. Пример выполнения задания 5………………………………. 69
4.5. Указания к заданию 6…………..……………………………………71
4.5.1. Основные теоретические положения…………………………71
4.5.2. Пример выполнения задания 6………………………………. 73
Список рекомендуемой литературы ………………………………………77
Указания к решению заданий по алгебре
И аналитической геометрии
Пример выполнения задания 1
Решить систему линейных уравнений

 .
.
а) методом Гаусса:
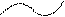



- к элементам первой и третьей строк прибавим соответствующие элементы второй строки:




- к элементам второй строки прибавим соответствующие элементы первой строки, умноженные на -4;
- к элементам третьей строки прибавим соответствующие элементы первой строки:




- элементы третьей строки разделим на 2:


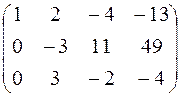

- к элементам третьей строки прибавим соответствующие элементы второй строки:



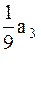
-элементы третьей строки разделим на 9:




- к элементам первой строки прибавим соответствующие элементы третьей строки, умноженные на 4;
- к элементам второй строки прибавим соответствующие элементы третьей строки, умноженные на -11:


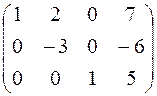

- элементы второй строки разделим на -3:




- к элементам первой строки прибавим элементы второй строки, умноженные на -2;

 .
.
Получаем 
б) по формулам Крамера:
Вычислим основной определитель системы

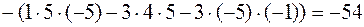 .
.
Вычислим вспомогательные определители системы:

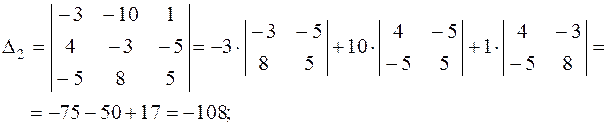

По формулам Крамера получаем

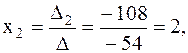

в) с помощью обратной матрицы:
Если обозначить
 - матрица коэффициентов при неизвестных,
- матрица коэффициентов при неизвестных,
 - столбец свободных членов,
- столбец свободных членов,
 - столбец неизвестных,
- столбец неизвестных,
то систему линейных уравнений можно записать в виде матричного уравнения
 .
.
Чтобы выразить Х из этого уравнения необходимо обе части этого уравнения умножить слева (!) на матрицу  (это возможно тогда и только тогда, когда А невырожденная, т.е.
(это возможно тогда и только тогда, когда А невырожденная, т.е.  ):
):
 .
.
Используя свойства умножения матриц, получаем
 ,
,

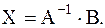
Найдем матрицу  с помощью присоединенной матрицы, причем
с помощью присоединенной матрицы, причем  существует, т.к.
существует, т.к.  , т.е.
, т.е.  . Для каждого элемента матрицы А найдем его алгебраическое дополнение:
. Для каждого элемента матрицы А найдем его алгебраическое дополнение:
 ,
,  ,
,
 ,
,
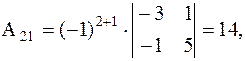





Получили, что
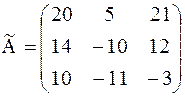 - присоединенная матрица,
- присоединенная матрица,
 ,
,
 - обратная матрица.
- обратная матрица.
Учитывая, что  , имеем
, имеем
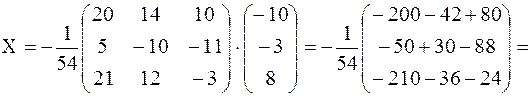
 ,
,
т.е.  или
или 
Ответ: 






