В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область комплексного переменного p:
p = α + j ω.
При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор p, что существенно упрощает расчет, так как сводит систему ДУ к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике.
Различают прямое преобразование Лапласа
(4.25)
и обратное преобразование Лапласа
. (4.26)
Функция F (p), определяемая уравнением (4.25), носит название изображения по Лапласу, а функция f (t) в (4.26) – оригинала. Комплексное число p называют оператором преобразования Лапласа. Следовательно, оригинал и изображение представляют собой пару функций действительного f (t) и комплексного F (p) переменного, связанных преобразованием Лапласа. Для сокращенной записи преобразований (4.25), (4.26) используют следующую символику:
f (t) ÷ F (p); f (t) ↔ F (p) и др.
Свойство линейности преобразования Лапласа можно записать в форме
(4.27)
где ak – постоянные коэффициенты разложения.
Дифференцирование оригинала. При ненулевых начальных условиях: f (–0) ≠ 0 дифференцирование оригинала соответствует следующему условию
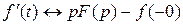. (4.28)
Как видно, операция дифференцирования оригинала при преобразовании Лапласа заменяется операцией умножения изображения на p.
Интегрирование оригинала.
. (4.29)
Операция интегрирования оригинала при преобразовании Лапласа заменяется операцией деления изображения на p.
Изображение операторной функции F (p) линейной цепи может быть представлено в виде отношения двух полиномов от p, не имеющих общих корней
, (4.30)
причем степень полинома знаменателя N (p) выше, чем степень полинома числителя M (p).
Нахождение оригинала по изображению с помощью
Теоремы разложения
Будем считать, что полиномы M (p) и N (p) выражения (4.30) не имеют общих корней, а уравнение N (p) = 0 не имеет кратных корней.
Для нахождения оригинала f (t) разложим M (p) на простые дроби:
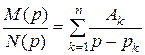, (4.31)
где pk – простые корни характеристического уравнения
, (4.32)
Ak – коэффициенты разложения.
В математике доказывается, что коэффициенты Ak можно определить по формуле
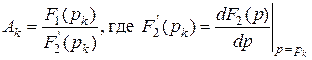. (4.33)
Подставив значения Ak в формулу (4.31) и осуществив ряд преобразований, окончательно получим формулу оригинала по заданному изображению
. (4.34)
Формула (4.34) является математической формулировкой теоремы разложения и позволяет найти оригинал по изображению в виде (4.30), в случае простых корней.
Если среди корней pk имеется один нулевой корень, т.е. F 2(p) = p F 3(p), то теорема разложения примет вид
. (4.35)
Если среди корней уравнения (4.32) (полюсов функции F (p)) имеются комплексно-сопряженные корни p k, k+1 = –α ± j ωсв, то в формуле (4.34) появится составляющая в виде затухающего гармонического колебания:
2·[ A cos(ωсв t) + B sin(ωсв t)] e – α t, (4.36)
где A и B – коэффициенты, определяемые по формуле:
. (4.37)
