Примером цепей первого порядка являются простейшие RL и RC цепи. Рассмотрим включение источника постоянного напряжения u (t) = E 0 к RL двухполюснику (рис. 4.2).
Из рис. 4.2 следует, что до коммутации ключ K разомкнут, поэтому ток
iL (–0) = 0 и цепь находится при нулевых начальных условиях. В момент t = 0 ключом K замыкаем (осуществляем коммутацию) цепь, подключив ее к источнику напряжения u (t) = E 0. После замыкания ключа в цепи начнется переходный процесс.
Для его математического описания выберем в качестве независимой переменной ток через индуктивность iL = i и составим относительно нее дифференциальное уравнение по второму закону Кирхгофа:
. (4.8)
Уравнение (4.8) является линейным неоднородным ДУ первого порядка, решение которого можно записать согласно (4.3) в форме:
i = i пр + i св, (4.9)
где i св – свободная составляющая тока, обусловленная свободными процессами, протекающими в цепи без источника u (t); i пр – принужденная составляющая тока, обусловленная действием источника u (t).
Свободная составляющая тока i св есть общее решение однородного ДУ
Согласно (4.5)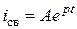 
, где A – постоянная интегрирования; p – корень характеристического уравнения типа (4.4);
pL + R = 0.
Отсюда p = –R/L. Величина 1/ p = τ носит название постоянная времени цепи. В данном примере RL цепи τ = L/R.
Принужденная составляющая i пр может быть определена как частное решение уравнения (4.8). Однако, как было указано выше, i пр можно найти более просто методами расчета установившегося режима цепи.
При включении в цепь постоянного напряжения (ω = 0) в цепи будет протекать постоянный ток (ω = 0), при котором сопротивление индуктивности равно нулю: xL = ω L = 0. Следовательно, установившийся ток в RL контуре равен i пр = E 0/ R.
Для нахождения постоянной интегрирования A перепишем (4.9) в форме 
и учтем начальные условия для тока через индуктивность, а также первый закон коммутации:
i (–0) = iL (0) = 0 = A + E 0/ R
Отсюда A = – E 0/ R. Таким образом, закон изменения тока в RL контуре определяется уравнением
. (4.10)
Напряжение на индуктивности равно
. (4.11)
На рис. 4.3 изображены графики зависимостей нормированных значений тока īL = iL / (E 0/ R) и напряжения ūL = uL/E 0 в RL- цепи.
Анализ полученных уравнений (4.10) и (4.11) показывает, что чем больше постоянная времени цепи τ, тем медленнее затухает переходный процесс. На практике принято считать переходный процесс законченным при t = (3 …5)τ. При t = 3τ ток достигает 95% своего установившегося значения, а при t = 5τ – более 99%. Графически постоянная времени τ может определяться как интервал времени на оси t от t = 0 до точки пересечения касательной к uL (рис. 4.3). В указанный момент времени напряжение на uL уменьшается в e раз по сравнению с начальным.
Анализ полученных результатов показывает, что при нулевых начальных в момент t = 0 индуктивность ведет себя как бесконечно большое сопротивление (разрыв цепи), а при t = ∞ как бесконечно малое сопротивление (короткое замыкание цепи).
Следует добавить, что при нулевых начальных в момент t = 0 емкость ведет себя как бесконечно малое сопротивление (короткое замыкание цепи), а при t = ∞ как бесконечно большое сопротивление (разрыв цепи).
Рассмотренный пример показывает, что в цепи первого порядка переходный процесс носит апериодический (не колебательный) характер.
