Входные и передаточные параметры контура (АЧХ) существенно зависят от частоты. Если через контур пропустить сумму гармонических колебаний различных частот, но одинаковой амплитуды, то на выходе контура амплитуды гармонических колебаний отклика на разных частотах изменятся не одинаково. Контур как бы «пропускает» колебания одних частот и не «пропускает» колебания других частот.
Способность цепи выделять колебания отдельных частот из суммы колебаний различных частот называется избирательностью.
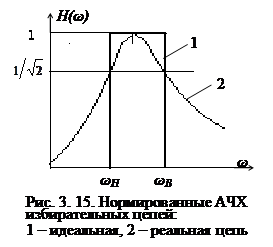В идеальном случае АЧХ цепи должна иметь прямоугольную форму, т.е. параметр цепи H (ω) должен иметь постоянное значение в определенном диапазоне частот, называемым полосой пропускания цепи, и быть равным нулю за пределами этого диапазона (рис. 3. 15, кривая 1). АЧХ реальных цепей, в том числе и АЧХ последовательного колебательного контура (рис. 3. 15, кривая 2), отличаются от характеристик идеальной избирательной цепи отсутствием резкой границы между областью пропускаемых и подавляемых колебаний. Очевидно, избирательные свойства реальной цепи тем выше, чем ближе к прямоугольной форме их нормированные АЧХ.
Значения частот, определяющих границу областей пропускаемых и подавляемых колебаний, называют граничными частотами:
ωн – нижняя граничная частота;
ωВ – верхняя граничная частота (рис. 3. 15).
Диапазон частот между граничными частотами называют полосой пропускания:
S = ωВ – ωН.
На практике чаще всего полосу пропускания находят на уровне, когда амплитуда отклика составляет 
от максимального значения (или в 
от минимального значения).
Для определения полосы пропускания запишем выражение модуля комплексного сопротивления контура (3.25) для граничных частот ωГР:
.
Используя выражение обобщенной расстройки a (ω) (3.23) для двух граничных частот, получим два уравнения:
.
Решение этих уравнений дает значения граничных частот полосы пропускания, которые симметричны относительно резонансной частоты:
. (3.33)
На основании определения полосы пропускания можно вывести формулу полосы пропускания
. (3.34)
Из выражения (3.34) следует, что полоса пропускания контура при фиксированном значении резонансной частоты ω0 обратно пропорциональна его добротности и не зависит от емкости C.
На рис. 3. 12, для Z (ω) и рис.3.13, 3.14 для KU (ω) видно, что с уменьшением добротности полоса пропускания возрастает и избирательность уменьшается.
Для оценки избирательности свойств реальной цепи используют такие параметры, которые оценивают степень отклонения формы ее АЧХ от прямоугольной. В частности, для этого вводят параметр коэффициент прямоугольности К П. Коэффициент прямоугольности определяется как отношение полосы пропускания контура на уровне 0.7Kmax к полосе пропускания на уровне 0.3Kmax:
.
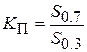Для идеального контура K П = 1, у реальных контуров K П < 1.
