ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
И РЕЗОНАНСНЫЕ ЯВЛЕНИЯ В ЦЕПЯХ
КОМПЛЕКСНЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Комплексные передаточные функции линейных цепей
Рассмотрим случай, когда воздействие на линейную цепь является гармоническим 
. Отклик линейной цепи на это воздействие тоже будет гармоническим с частотой воздействия 
.
Важнейшей характеристикой линейной цепи является комплексная передаточная функция H (j ω) ( КПФ ). При этом электрическую цепь удобно изображать в виде четырехполюсника (рис. 3.1). Внешние полюса (1 – 1/), на которые действует воздействие в виде напряжения с комплексной амплитудой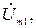 
или тока с комплексной амплитудой 
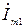, называются входными полюсами.
Внешние полюса (2 – 2/), к которым подключают нагрузку, т.е. полюса, с которых снимается реакция (отклик) в виде напряжения с комплексной амплитудой 
или тока с комплексной амплитудой 
, называются выходными полюсами.
Комплексная передаточная функция (КПФ) определяется как отношение комплексной амплитуды реакции цепи к комплексной амплитуде внешнего воздействия (рис. 3.1)
. (3.1)
В зависимости от вида воздействия и 
отклика (см. рис. 3.1) различают следующие виды КПФ:
1. Комплексная передаточная функция по напряжению или коэффициент передачи по напряжению
. ( 3.2 )
2. Комплексная передаточная функция по току или коэффициент передачи по току
. (3.3)
3. Комплексное передаточное сопротивление или передаточное сопротивление
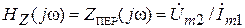. (3.4)
4. Комплексная передаточная проводимость или передаточная проводимость
. (3.5)
Первые две функции (3.2) и (3.3) являются безразмерными величинами, а функции (3.4) и (3.5) – имеют соответственно размерности сопротивления и проводимости.
Комплексные частотные характеристики
Всякую комплексную величину H (j ω) можно представить в показательной, тригонометрической и алгебраической форме (3.6):
;
; (3.6)
.
Величина H( ω) = │H (j ω) │ является модулем передаточной функции.
Зависимость модуля комплексной передаточной функции от частоты называется амплитудно-частотной характеристикой цепи (АЧХ) КПФ (рис. 3.2, а).
Величина φH(ω) = arg H (j ω) – аргумент комплексной передаточной функции. Зависимость φ(ω) от частоты называют фазо-частотной характеристикой цепи (ФЧХ) КПФ (рис. 3.2, б).
Величины
(3.7)
есть вещественная и мнимая части комплексной передаточной функции.
Из (3.6) и (3.7) можно получить выражения модуля (АЧХ) и аргумента (ФЧХ) комплексной передаточной функции
; (3.8)
. (3.9)
 |
АЧХ и ФЧХ цепи можно изобразить единым графиком, если построить зависимость КПФ H (j ω) от частоты ω на комплексной плоскости. При этом конец вектора H (j ω опишет некоторую кривую, которая называется годографом комплексной передаточной функции (рис. 3.2, в). На годографе указывают точки, соответствующие некоторым значениям частоты ω, и стрелкой показывают направление перемещения конца вектора при увеличении частоты.
Совокупность АЧХ, ФЧХ и годограф составляет комплексные частотные характеристики (КЧХ). КЧХ являются наиболее фундаментальными понятиями теории цепей и широко используются на практике.
В ряде случаев частотные характеристики цепи могут изменяться в очень широких пределах, поэтому более удобно их оценивать в логарифмическом масштабе. С этой целью для оценки АЧХ вводят понятие логарифмической амплитудно-частотной характеристики (ЛАХ):
K = 20lg H (ω).
Оценивается ЛАХ в децибелах (дБ). В активных цепях K называют еще логарифмическим усилением. Для пассивных цепей вместо коэффициента усиления оперируют ослаблением цепи
A = 20lg[1/ H (ω)],
которое также оценивается в децибелах.
