С одним реактивным элементом

 

В радиотехнике широкое применение находят делители напряжения, построенные по схеме Г- образного четырехполюсника (рис.3.6). Если известен комплексный коэффициент передачи по напряжению 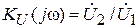, то можно определить выходное напряжение при заданном входном напряжении и коэффициенте передачи по напряжению:

Комплексный коэффициент передачи по напряжению в режиме холостого хода на выходе (İ₂ = 0) можно определить по закону Кирхгофа для контура и по закону Ома:

. (3.10)

В схеме на рис. 3.6, меняя элементы Z₁ и Z₂, и оставляя одно из этих сопротивлений чисто реактивным, а другое резистивным, можно построить четыре разных схем четырехполюсников, изображенных на рис. 3.7.

 

 

Используя выражение (3.10), можно записать комплексный коэффициент передачи по напряжению для всех четырех схем, подставляя соответствующие значения Z₁ (j ω)и Z₂ (j ω).

Рассмотрим в качестве примера схему на рис. 3.7, а – RL– делитель.

Подставив Z₁ (j ω) = R и Z₂ (j ω) = j ω L в формулу (3.10), получим комплексный коэффициента передачи по напряжению K_U (j ω) (3.11):модуль K_U (ω) – АЧХ, аргумент φ _U (ω) – ФЧХ, действительную K₁ (j ω)и мнимую K₂ (j ω)части для построения годографа:

(3.11)

Непосредственное использование выражений (3.11) для построения КЧХ неудобно, так как для каждой пары значений параметров R и L необходимо строить отдельную кривую. Построение существенно упрощается при замене абсолютных значений частоты ω, комплексного коэффициента передачи K_U (j ω ) и модуля K_U (ω) относительными (нормированными) значениями:

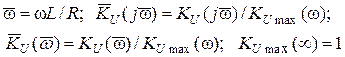. (3.12)

Из выражений (3.12) следует, что все нормированные параметры являются безразмерными величинами. Запишем нормированные выражения АЧХ, ФЧХ, реальной и мнимой частей:

(3.13)

Нормированные параметры упрощают процесс сравнения характеристик цепей с разными параметрами.

В практике решения радиотехнических задач часто приходится проводить численный расчет различных характеристик цепей, в т.ч. частотных. На рис. 3.8 показаны нормированные частотные характеристики RL- четырехполюсника, рассчитанные по формулам (3.13).

В области сравнительно низких частот (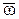 << 1), когда полное сопротивление индуктивности ω L значительно меньше R, коэффициент передачи по напряжению (см. (3.12)), близок к 0, т.е. выходное напряжение делителя значительно меньше входного по амплитуде.

 

В области верхних частот 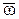>> 1, когда полное сопротивление индуктивности ω L значительно меньше R, коэффициент передачи по напряжению (см. (3.12)), близок к 1, т.е. выходное напряжение делителя близкое к входному по амплитуде.

На основе рассмотренного примера можно сделать общий для реальных цепей вывод: если цепь содержит реактивные элементы (L, C), то входные и передаточные параметры цепи будут частотно-зависимыми.