Все решаемые задачи в геометрии недр делятся на два вида: позиционные и метрические. К позиционным задачам относятся изображение формы залежи, горных выработок, поверхности земли, кровли и почвы залежи и другие. К метрическим задачам относятся определение параметров и элементов залегания залежи в горном массиве. Установление линий пересечения залежи с различными слоями горных пород, определение различных геометрических параметров и размеров различных тектонических нарушений, смещений и другие сведений. Метрические задачи решают различными аналитическими и геометрическими методами. Важными условиями при графическом изображении различных объектов являются:
- наглядность – это по графическому изображению (на планах или разрезах) без особого труда представить пространственную модель горно-геологического объекта. Легко определить параметры и элементы залежи, и детально распознать внутреннее устройство объекта с наименьшим перекрытием.
– простата построения – это выбор правильной системы изображения различных объектов на плоскости проекции для построения планов и разрезов.
- удобоизмеряемость – это на планах и разрезах, где выполнены изображения объекта, можно легко производить измерения параметров и элементов залегания для решения метрических задач с определенной степенью точности.
- динамичность – это возможность систематического пополнения маркшейдерских графических материалов в соответствии с развитием горных и разведочных работ.
к онтрастность – это возможность четкого чтения изображения и отбора необходимой информации для работы на специальных приборах и компьютерах.
Выбор масштаба графического изображения объекта является важным условием при решении позиционных и метрических задач.
Масштаб чертежа (плана или разреза) равна:
M= а/Д,
где а – максимальная ошибка графических построений, равная 0,2-0,3 мм; Д – необходимая точность определения исходного расстояния, мм.
Пример 1. Пусть длина l= 120 м. Относительная погрешность определения 1:1000. Установить масштаб чертежа.
Д = 120/1000 = 0,12 м = 120 мм.
М = 0,3/120 = 1/400 или ближайший масштаб по ГОСТу 1:500.
Для графического изображения различных объектов применяют два метода проекций: центральный и параллельный.
Сущность центрального или конического метода проекций заключается в следующем: например, возьмем горизонтальную плоскость Н и точку S в пространстве, которую назовем полюсом и не принадлежащая плоскости Н. Возьмем некоторую точку А, находящуюся между полюсом S и плоскостью Н (рис. 4,а). Проведем из полюса S через точку А некоторый луч до пересечения его с плоскостью Н и получим на ней точку а.
Здесь плоскость Н называют плоскостью проекций, точку S - центром проецирования, точку а - центральной проекцией точки А на плоскости Н, луч SА - проецирующим лучом.
С помощью этого метода можно спроецировать на плоскость прямую, кривую, любой геометрический объект.. Для этого достаточно найти несколько проекций точек, принадлежащих заданной прямой (рис. 4,6) или кривой (рис.4,в) линии или другой геометрической формы (рис.4,в) и соединить их.
Рис.4. Центральный метод проецирования: а- точки; б-прямой; в- кривой.
Параллельный метод проецирования является частным случаем центрального проецирования. Полученные с помощью такого метода проецирования проекции называются параллельными (рис.5).
Рис.5. Метод параллельного проецирования:
а- прямой; б- геометрической фигуры.
При параллельном проектировании прямой АВ или плоскости АВС на горизонтальную плоскость Н, то получим их проекции без искажения. Параллельный метод проецирования широко применяется в практике. При этом методе графическое отображение изучаемого объекта учитывают два основных требования: наглядность и удобоизмеряемость.
Если же проецирующие лучи направить перпендикулярно к плоскости проекций то получим прямоугольный метод проецирования или ортогональный. Когда проецирующие лучи направлены под острым углом к плоскости проекций, получаем косоугольный метод проецирования.
Проекции с числовыми отметками. Сущность метода проекций с числовыми отметками заключается в том, что на некоторую плоскость, называемую плоскостью проекций, ортогонально проектируются точки, принадлежащие некоторым элементам или пространственному телу. На плоскости проекций получают изображение проектируемых элементов или тела в двух измерениях. Третьим измерением являются числовые отметки точек.
Числовой отметкой называют расстояние по нормали от проектируемой точки до плоскости проекций. За основную плоскость проекций в практике чаще всего применяется горизонтальная.
На рис.6 показано изображение точек в проекциях с числовыми отметками. В пространстве взяты произвольные точки А и В и горизонтальная плоскость Н. Точка С взята на плоскости и ее числовая отметка равна нулю. Проекции точки 
, В провести перпендикулярные к плоскости линии до пересечения с ней, то получим прямоугольные проекции точек а, b на плоскости Н. Нетрудно видеть, что точка С совпадает со своей проекцией с0, и лежит на плоскости проекции. Числовые отметки точек, расположенных над плоскостью проекций, считаются положительными, ниже плоскости -отрицательными. Знак минус пишется только у отрицательных числовых отметок.
Рис. 6. Проецирование точек на горизонтальную плоскость проекций:
а - точки А и В расположены вне плоскости проекций; б - точка С на плане.
Часто некоторые объекты проецируются на вертикальную плоскость V (рис.7). На рис. 7 показан способ проецирования точек Д и Е на вертикальную плоскость. При этом отрицательные отметки имеют точки, расположенные за плоскостью проекций.
Рис. 7. Проецирование точек на вертикальную плоскость проекций.
Если горизонтальную или вертикальную плоскости проекций принимают за любую условную плоскость, то числовые отметки называют условными отметками (относительными).
Проекции точек и прямых линий. В практике часто некоторые выработки принимают за точку и прямую линию. Это скважины и горных выработки, линии простирания и падения залежей полезного ископаемого, горных пород и другие.
Отрезок прямой на плане в проекциях с числовыми отметками может быть задан координатами двух точек а16,2 и в48,2 прямой (ав) (рис. 8,а), координатами одной точки с10,5 и направлением прямой под дирекционным углом α (рис. 8,6) и углом падения прямой β (рис. 8,в).
Рис. 8. Изображение отрезка прямой линии в проекциях с числовыми отметками.
Углом направления α прямой называется угол между северным направлением оси х и направлением прямой в сторону ее понижения, отсчитываемый по ходу часовой стрелки. Углом наклона β называется угол падения прямой к горизонту. В зависимости от знака угла наклона различают угол восстания (+ β) и угол падения (- β). Углы восстания и падения численно равны. На рис. 9 показана прямая АВ. Отрезок СВ этой прямой имеет угол падения δ, а отрезок СА этой же прямой - угол восстания, равный также δ.
Рис. 9. К определению угла наклона прямой
Тангенс угла наклона прямой называется уклоном прямой, т.е.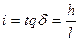 
. Проекция прямой на горизонтальную плоскость Н между двумя точками называется заложением l.
При решении различного характера задач в геологии, маркшейдерии и горном деле пользуются уклоном прямой, заложением и высотой сечения h этой прямой.
Градуированием прямой называется определение на проекции прямой точек с дискретными (или кратными) числами, равные высоте сечения. Например, кратными числами могут быть 0,5, 1, 2,5 м и т.д.
Градуирование прямой может быть выполнено на глаз, с помощью трафарета или аналитическими способами. Аналитический способ градуирования прямой заключается в следующем: Пусть на рис. 10 дан в плане отрезок a16b25.
Рис. 10. Аналитический способ градуирования прямой
Требуется этот отрезок проградуировать при h =1м. Допустим, что длина отрезка a16b25 (горизонтальное положение) составляет 36мм. Величина заложения l на 1 м превышения определяется из соотношения:
Отсюда: 
Тогда отрезком в 4 мм и градуируется прямая a16b25. Если данные точки имеют дробные или некратные заданному числу отметки, то предварительно находят на прямой точку с целыми или кратными величине h числовыми отметками.
Графический способ градуирования может быть выполнен двумя способами: способ профиля и способ трафарета.
Способ профиля (рис.11,а). Градуирование указанным способом проводится с помощью миллиметровой бумаги. Отрезок прямой a3,4b8,5 необходимо проградуировать через 1 м.
Рис. 11. Графический способ градуирования прямой: а- способом профиля; б- способом трафарета.
Способ трафарета (палетки) (рис.11,б). На кальке или на прозрачной бумаге строят трафарет (или палетку), т.е. проводят ряд параллельных линий на одинаковом расстоянии. Расписывают палетку через заданную высоту сечения h =1 м. Накладывают ее на данный отрезок (а12,6в19,5) таким образом, чтобы отметка точки а12,6 на плане совпадала с отметкой на палетке. Закрепляют палетку иголкой в точке а12,6 и вращают ее до тех пор, пока она не займет положение, при котором отметка точки в19 на плане будет соответствовать такой же отметке на палетке. Закрепляют палетку в таком положении и, приложив к линии линейку, делают легкие наколы точек пересечения линии палетки с отрезком a12,6b19,5 (точки 14,16,18 м). Снимают палетку, и у точек накола выписывают отметки соответствующих линий палетки.
Взаимное положение прямых. Две прямые в пространстве могут пересекаться,скрещиваться, быть параллельными.
Прямые параллельны между собой, если параллельны их проекции, заложения равны, числовые отметки возрастают в одну сторону (рис. 12,а).
Прямые пересекаются, если пересекаются их проекции, а точка пересечения К17,5 для обеих прямых имеет одну и ту же числовую отметку (рис. 12,б).
Прямые скрещиваются, если проекции прямых пересекаются, но в точке пересечения имеют разные отметки; проекции прямых параллельны, но имеют разные заложения, или имеют одинаковое заложение, но возрастание отметок идет в разные стороны (рис. 12,в).
Рис. 12. Взаимное положение прямых.
Взаимное положение плоскостей. Плоскость в пространстве и ее изображение на плане может быть определена следующими элементами:
1) тремя точками, не лежащими на одной прямой;
2) прямой линией и точкой, находящейся вне этой прямой;
3) двумя пересекающимися прямыми;
4) двумя паралле льными прямыми.
Плоскость может быть изобрежена в горизонталях (рис.13).
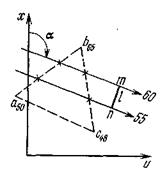
Рис. 13. Изображение плоскости в горизонталях.
Плоскости в пространстве могут пересекаться и быть параллельными.
Пересекающиеся плоскости. Две плоскости пересекаются в пространстве, если соблюдается одно из следующих условий: а) одноименные горизонтали обеих плоскостей пересекаются; б) горизонтали заданных плоскостей параллельны и имеют противоположное направление; в) горизонтали заданных плоскостей параллельны, имеют одно направление, но заложения этих плоскостей неодинаковы по величине.
Пример 1: Пусть заданы две плоскости Р1 и Р2 (рис. 14). Определить линию пересечения плоскостей Р1 и Р2. и ее элементы залегания.
По заданным геометрическим элементам плоскости Р1 и Р2. изображают в проекциях с числовыми отметками в виде горизонталей (рис.14,а). Одноименные горизонтали плоскостей пересекаются в точках а и б. Соединив точки а и б, получим линию пересечения плоскостей Р1 и Р2. Графически измеряется угол простирания (
)линии пересечения.
Для определения угла падения строится вспомогательный разрез (рис.15,6). На разрезе по заложению d=аб линии пересечения и высоте сечения горизонталей h= 80-70=10 м.
Рис.14. Построение линии пересечения двух плоскостей.
Пример 2: Пусть в проекциях с числовыми отметками заданы плоскости Р1 и Р2. (рис. 15,а). Горизонтали их пересекаются за пределами чертежа. Линию пересечения плоскостей Р1 и Р2 можно определить по способу вертикальных разрезов.
Рис. 15. Построение линии пересечения двух плоскостей при условии, если их одноименные горизонтали пересекаются за пределами чертежа
На рис.16 приведено решение аналогичной задачи, если горизонтали заданных плоскостей Р1 и Р2 направлены в одну сторону.
Рис. 16. Построение линии пересечения двух плоскостей при условии, что горизонтали направлены в одну сторону: а - план; б и в – вспомогательные разрезы.
Взаимное положение прямой и плоскости. Прямая линия и плоскость могут иметь следующее взаимное расположение: 1) прямая принадлежит плоскости; 2) прямая пересекает плоскость; 3) прямая параллельна плоскости.
Прямая принадлежит плоскости, если все три координаты двух ее точек совпадают с координатами точек заведомо принадлежащих плоскости (рис. 17,а).
Простирание прямой, расположенной в заданной плоскости, может иметь любое значение от 0 до 360°, а угол наклона прямой к горизонту может изменяться от 0° до 900. В геолого-маркшейдерской часто встречаются различные виды задач.
Например: Пусть дана плоскость в проекциях с числовыми отметками и на ней прямая а5в2 (рис. 17а,6). Определить угол наклона ab. Нетрудно видеть, что отрезок представляет собой заложение прямой ab на h =10 м. По заложению la и превышению h строится прямоугольный треугольник, в котором определяется угол наклона заданной прямой б (рис. 17,в).
Рис.17.Прямая, принадлежащая плоскости.
Лекция 3. Аксонометрические, аффинные и векторные проекции. Топографические поверхности в проекциях с числовыми отметками и способы их построения. Математические действия с поверхностями топографического порядка.
Сущность метода параллельного аксонометрического проецирования заключается в том, что данная точка, плоская фигура или геометрическое тело вместе с осями прямоугольных координат, к которым они отнесены в пространстве, проецируются на плоскость Р, называемую плоскостью аксонометрических проекций (рис.18).
Пусть ох, оу, ох - оси прямоугольных координат в пространстве, а о1хр, о1ур, о1zр - их проекции на плоскости Р, называемые аксонометрическими осями. В пространстве отложен отрезок t, принимаемый за единицу измерения по этим осям. Отношения tx/t=p, ty/t=q, tz/t=r
называются коэффициентами искажения по аксонометрическим осям.
Рис. 18. Схема аксонометрического проецирования точки.
Показатели искажения p,q и r характеризуют степень искажения всех отрезков прямых, параллельных соответствующим аксонометрическим осям. В зависимости от соотношения коэффициентов искажения аксонометрические проекции могут быть:
изометрическими, если коэффициенты искажения по всем трем осям равны между собой, т.е. p=q=r;
диметрическими, если коэффициенты искажения по двум осям равны между собой, а третий не равен первым двум. Могут быть три разновидности диметрических проекций, в которых p=q¹r; p=q¹r; p=q=r
триметрическими, если все три коэффициента искажения не равны между собой, т.е. p¹q; p¹r;q¹r.
В изометрической проекции p=q=r =0,82. Это значит, что по каждой из аксонометрических осей показатели искажения равны 0,82.
В диметрической проекции два коэффициента искажения равны между собой, а третий не равен, т.е. p=r=0,94, а q=1/2p=0,47. В триметрической проекции задают два показателя искажения, а третий вычисляют по специальной формуле.
Расположение осей прямоугольной изометрии и диметрии показано на рис. 19,а и б. В изометрической проекции все три угла равны между собой и составляют 120°.
Рис.19. Расположение аксонометрических осей.
В аксонометрической проекции изображена горные выработки (рис.20).
Рис.20. Изображение горных выработок в аксонометрической проекции.
Аффинные проекции это один из видов параллельного проецирования. Геометрическую основу аффинных проекций дает известное в аналитической геометрии родственное, или аффинное проекции(рис.21).
Рис.21. Схема аффинного проецирования.
Векторные проекции - это пространственное изображение объекта, сохраняющее измеримость в горизонтальных плоскостях1 и называются методом параллельных векторов. Геометрическая сущность данного метода заключается в том, что точки пространства изображают с помощью параллельных векторов по заранее заданному направлению S (рис.22,а).
Рис. 22. Схема векторного изображения.
