2.13. На дифракционную решетку нормально падает монохроматический свет с длиной волны 600 нм. Определить наибольший порядок спектра, полученный с помощью этой решетки, если ее постоянная равна 2 мкм. [3].
2.14. На дифракционную решетку длиной 1,5 см, содержащую 3000 штрихов, падает нормально монохроматический свет с длиной волны 550 нм. Определить число максимумов, наблюдаемых в спектре дифракционной решетки. [19].
2.15. Определить число штрихов на 1 мм дифракционной решетки, если углу j=30° соответствует максимум четвертого порядка для монохроматического света с длиной волны 0,5 мкм. [250 мм-1].
2.16. Период дифракционной решетки 0,005мм. Определить число наблюдаемых главных максимумов в спектре дифракционной решетки для: 1) l= 760 нм; 2) l= 440 нм. [1) 13; 2) 23].
2.17. Сколько штрихов на 1 мм должна иметь дифракционная решетка, чтобы углу j = 90° соответствовал максимум 5-го порядка для света с длиной волны l = 500 нм? [400].
2.18. На дифракционную решетку с периодом 0,004 мм падает нормально монохроматический свет. При этом главному максимуму четвертого порядка соответствует отклонение от первоначального направления на j = 30°. Определить длину волны света. [0,5 мкм].
2.19. Длина волны красной линии кадмия равна 6438 Å. Каков угол отклонения линии в спектре первого порядка, если дифракционная решетка имеет 5684 штриха на 1 см? Сколько добавочных минимумов образуется между соседними главными максимумами? Ширина решетки 5 см. [21°28¢, 28419].
2.20. Монохроматический свет (l=0,6 мкм) падает нормально на дифракционную решетку, содержащую 400 штрихов на 1 мм. Определить угол отклонения, соответствующий максимуму наивысшего порядка. Найти общее число дифракционных максимумов, которые дает эта решетка. [73,7°; 9].
 2.21. На дифракционную решетку нормально к ее поверхности падает параллельный пучок лучей (l=0,5 мкм). Помещенная вблизи решетки линза проектирует дифракционную картину на плоский экран, удаленный от линзы на
2.21. На дифракционную решетку нормально к ее поверхности падает параллельный пучок лучей (l=0,5 мкм). Помещенная вблизи решетки линза проектирует дифракционную картину на плоский экран, удаленный от линзы на 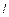 = 1 м (рисунок). Расстояние между двумя максимумами первого порядка, наблюдаемыми на экране, s = 20,2 см. Определить: а) постоянную дифракционной решетки; б) число штрихов на 1 см; в) теоретически возможное число максимумов, которые способна дать решетка; г) угол отклонения лучей, соответствующий последнему дифракционному максимуму. [а) 4,95 мкм; б) 2020 см-1; в) 19; г) 65°24¢].
= 1 м (рисунок). Расстояние между двумя максимумами первого порядка, наблюдаемыми на экране, s = 20,2 см. Определить: а) постоянную дифракционной решетки; б) число штрихов на 1 см; в) теоретически возможное число максимумов, которые способна дать решетка; г) угол отклонения лучей, соответствующий последнему дифракционному максимуму. [а) 4,95 мкм; б) 2020 см-1; в) 19; г) 65°24¢].
2.22. На дифракционную решетку нормально падает монохроматический свет с длиной волны 0,5 мкм. На экран, находящийся от решетки на расстоянии 1 м, с помощью линзы, расположенной вблизи решетки, проецируется дифракционная картина, причем первый главный максимум наблюдается на расстоянии 15 см от центрального. Определить число штрихов на 1 см дифракционной решетки. [30 см-1].
2.23. На дифракционную решетку нормально к ее поверхности падает монохроматический свет с длиной волны 550 нм. На экран, находящийся от решетки на расстоянии 1 м, с помощью линзы, расположенной вблизи решетки, проецируется дифракционная картина, причем первый главный максимум наблюдается на расстоянии 12 см от центрального. Определить: 1) период дифракционной решетки; 2) число штрихов на 1 см ее длины; 3) общее число максимумов, даваемых решеткой; 4) угол дифракции, соответствующий последнему максимуму. [1) 4,58 мкм; 2) 2,18×103 см-1; 3) 17; 4) 73,9°].
2.24. На дифракционную решетку падает нормально свет. При этом максимум второго порядка для линии l1 = 0,65 мкм соответствует углу j1=45°. Найти угол, соответствующий максимуму третьего порядка для линии l2=0,50 мкм. [54°40¢].
2.25. Имеется дифракционная решетка с 500 штрихами на 1 мм, освещаемая фиолетовым светом (l=0,4 мкм). Определить угловое расстояние между максимумами первого порядка. [23°6¢].
2.26. Определить длину волны монохроматического света, падающего нормально на дифракционную решетку, имеющую 300 штрихов на 1 мм, если угол между направлениями на максимумы первого и второго порядков составляет 12°. [644 нм].
2.27. Дифракционная решетка, имеющая 500 штрихов на 1 мм, дает на экране, отстоящем от линзы на 1 м, спектр. Определить, на каком расстоянии друг от друга будут находиться фиолетовые границы (l = 0,435 мкм) спектров второго порядка. [0,87 м].
2.28. На решетку с постоянной, равной 0,006 мм, нормально падает монохроматический свет. Угол между соседними спектрами первого и второго порядков Dj = 4°36'. Определить длину световой волны. При решении использовать приближенное равенство sinj» j. [0,48 мкм].
2.29. Найти наибольший порядок дифракционного спектра желтой линии натрия (l = 5890 Å) в дифракционной решетке, содержащей 200 штрихов на 1 мм. [8].
2.30. При освещении дифракционной решетки белым светом спектры второго и третьего порядков отчасти накладываются друг на друга. На какую длину волны в спектре второго порядка накладывается фиолетовая граница (l = 0,4 мкм) спектра третьего порядка? [0,6 мкм].
2.31. На дифракционную решетку нормально падает пучок света от газоразрядной трубки, наполненной гелием. На какую линию в спектре четвертого порядка накладывается красная линия гелия (lкр=6,7×10-5 см) спектра третьего порядка? [5,02×10-5 см].
2.32. Дифракционная решетка длиной 5мм может разрешить в первом порядке две спектральные линии натрия (l1= 589,0 нм и l2= 589,6 нм). Определить, под каким углом в спектре третьего порядка будет наблюдаться свет с l3= 600 нм, падающий на решетку нормально. [20°42'].
2.33. Монохроматический свет нормально падает на дифракционную решетку. Определить угол дифракции, соответствующий максимуму четвертого порядка, если максимум третьего порядка отклонен на 18°. [24°20'].
2.34. Определить постоянную дифракционной решетки, если она в первом порядке разрешает две спектральные линии калия (l1 = 578 нм и l2= 580 нм). Длина решетки 1 см. [34,6 мкм].
2.35. Постоянная дифракционной решетки длиной 2,5 см равна 5 мкм. Определить разность длин волн, разрешаемую этой решеткой, для света с длиной волны l = 0,5 мкм в спектре второго порядка. [50 пм].
2.36. Две дифракционные решетки имеют одинаковую ширину 3 мм, но разные периоды: d 1 = 3×10-3 мм и d 2=6×10-3 мм. Определить их наибольшую разрешающую способность для желтой линии натрия с длиной волны 5896 Å. [5000; 5000].
2.37. Дифракционная решетка имеет 1000 штрихов и постоянную 10 мкм. Определить: 1) угловую дисперсию для угла дифракции 30° в спектре третьего порядка; 2) разрешающую способность дифракционной решетки в спектре пятого порядка. [1) 3,46×105 рад/м; 2) 5000].
2.38. Определить длину волны, для которой дифракционная решетка с постоянной 3 мкм в спектре второго порядка имеет угловую дисперсию 7×105 рад/м. [457 нм].
2.39. На дифракционную решетку падает свет, длина волны которого l = 500 нм. Угловая дисперсия дифракционной решетки в спектре второго порядка равна 4,08×105 рад/м. Определить постоянную дифракционной решетки. [5 мкм].
2.40. Определить угловую дисперсию дифракционной решетки для l = 5890 Å в спектре первого порядка. Постоянная решетки 2,5×10-4 см. [4,16×105 рад/м].
2.41. Под углом 30° наблюдается четвертый максимум для красной линии кадмия (lкр=0,644 мкм). Определить постоянную дифракционной решетки и ее ширину, если она позволяет в условиях задачи различить Dl = 0,322 нм. [5,15 мкм; 3,57 мм].
2.42. Длины волн дублета желтой линии в спектре натрия равны 5889,95 и 5895,92 Å. Какую ширину должна иметь решетка, содержащая 600 штрихов на 1 мм, чтобы различить эти линии в спектре первого порядка? [1,65 мм].
2.43. Рентгеновское излучение с длиной волны l = 1,63 Å падает на кристалл каменной соли. Найти межплоскостное расстояние кристаллической решетки каменной соли, если дифракционный максимум первого порядка наблюдается при угле скольжения 17°. [2,79 Å].
2.44. Рентгеновское излучение с длиной волны 2 Å падает на монокристалл. Чему равен угол скольжения, если в спектре второго порядка получен максимум? Межплоскостное расстояние кристаллической решетки 0,3 нм. [41°49¢].
Поляризация света
2.45. 1. Определить угол полной поляризации отраженного света для воды (n = 1,33), стекла (n =1,6) и алмаза (n = 2,42); 2. Как поляризован падающий луч, если в этом случае отраженные лучи отсутствуют? [1)  =53°,
=53°, 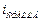 =58°,
=58°, 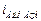 =67°30¢; 2) плоско поляризован].
=67°30¢; 2) плоско поляризован].
2.46. Угол преломления луча в жидкости 35°. Определить показатель преломления жидкости, если известно, что отраженный луч максимально поляризован. [1,4].
2.47. Свет падает под углом полной поляризации на границу раздела двух сред. Какой угол образуют между собой отраженный и преломленный лучи? [90°].
2.48. Предельный угол полного внутреннего отражения для некоторого вещества равен 60°. Чему равен для этого вещества угол полной поляризации? Какова скорость света в этом веществе? [49°6¢; 2,6×108 м/с].
2.49. Пучок естественного света падает на стекло с показателем преломления 1,73. Определить, при каком угле преломления отраженный от стекла пучок света будет полностью поляризован. [30°].
2.50. Два николя расположены так, что угол между их главными плоскостями составляет 60°. 1. Во сколько раз уменьшится интенсивность естественного света при прохождении его через один николь? 2. Во сколько раз уменьшится интенсивность света при прохождении через оба николя? При прохождении каждого из николей потери на отражение и поглощение составляют 5%. [1) 2,1; 2) 9,1].
2.51. Чему равен угол между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через эти призмы, уменьшилась в 4 раза? Поглощением света пренебречь. [45°].
2.52. Главные плоскости двух призм Николя, поставленных на пути луча, образуют между собой угол 60°. Как изменится интенсивность света, прошедшего через эти призмы, если угол между их плоскостями поляризации станет равным 30°? [Увеличится в 3 раза].
2.53. Во сколько раз ослабляется естественный свет, проходя через два николя, главные плоскости которых составляют угол 30°, если в каждом из николей на отражение и поглощение теряется 10% падающего на него светового потока? [3,3].
2.54. Между двумя скрещенными поляроидами размещается третий поляроид так, что его главная плоскость составляет угол 45° с главной плоскостью первого поляроида. Как изменится интенсивность естественного света, проходящего через такое устройство? Поглощением света в поляроидах пренебречь. [Уменьшится в 8 раз].
2.55. Пучок естественного света падает на систему из четырех николей, главная плоскость каждого из которых повернута на угол 60° относительно главной плоскости предыдущего николя. Во сколько раз уменьшится интенсивность света, проходящего через эту систему? Поглощением света пренебречь. [В 128 раз].
2.56. Угол между главными плоскостями поляризатора и анализатора составляет 30°. Определить изменение интенсивности прошедшего через них света, если угол между главными плоскостями равен 45°. [Уменьшится в 1,5 раза].
2.57. Интенсивность естественного света, прошедшего через два николя, уменьшилась в 8 раз. Пренебрегая поглощением света, определить угол между главными плоскостями николей. [60°].
2.58. Определить, во сколько раз ослабится интенсивность света, прошедшего через два николя, расположенные так, что угол между их главными плоскостями 60°, а в каждом из николей теряется 8% интенсивности падающего на него света. [В 9,45 раза].
2.59. Определить, во сколько раз уменьшится интенсивность естественного света, прошедшего через два николя, главные плоскости которых образуют угол в 60°, если каждый из николей как поглощает, так и отражает 5% падающего на них света. [В 9,88 раза].
2.60. Естественный свет проходит через поляризатор и анализатор, угол между главными плоскостями которых равен j. Поляризатор и анализатор как поглощают, так и отражают 10% падающего на них света. Определить угол, если интенсивность света, вышедшего из анализатора, равна 12% интенсивности света, падающего на поляризатор. [52°14'].
2.61. Узкий параллельный пучок рентгеновского излучения с длиной волны l = 245 нм падает на естественную грань монокристалла каменной соли. Определить расстояние между атомными плоскостями монокристалла, если дифракционный максимум второго порядка наблюдается при падении излучения к поверхности монокристалла под углом скольжения 61°. [0,28 пм].
2.62. Узкий параллельный пучок монохроматического рентгеновского излучения падает на грань кристалла с расстояниеммежду его атомными плоскостями 0,3 нм. Определить длину волны рентгеновского излучения, если под углом 30° к плоскости грани наблюдается дифракционный максимум первого порядка. [300 пм].
2.63. Кварцевая пластинка освещена монохроматическим светом определенной длины волны. Определить толщину кварцевой пластинки, для которой угол поворота плоскости поляризации j = 180°. Удельная постоянная вращения в кварце для данной длины волны [a] = 0,52 рад/мм. [6,04 мм].
2.64. Раствор глюкозы с массовой концентрацией 0,21 г/см3, находящийся в стеклянной трубке, поворачивает плоскость поляризации монохроматического света, проходящего через раствор, на угол 24°. Определить массовую концентрацию глюкозы в другом растворе в трубке такой же длины, если он поворачивает плоскость поляризации на угол 18°. [157 кг/м3].
2.65. Определить толщину кварцевой пластинки, для которой угол поворота плоскости поляризации света с длиной волны l=500 нм равен 48°. Постоянная вращения кварца для этой длины волны a= 30°/мм. [1,6 мм].
2.66. Определить удельное вращение раствора сахара, концентрация которого 0,33 г/см3, если при прохождении монохроматического света через трубку с раствором угол поворота плоскости поляризации 22°. Длина трубки 10 см. [6,67°×см2/г].
3. КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ
Основные формулы и законы
· Поток энергии  , т.е. энергия, излучаемая (или поглощаемая) телом за единицу времени:
, т.е. энергия, излучаемая (или поглощаемая) телом за единицу времени:

где  – энергия, излучаемая (или поглощаемая) телом во всем диапазоне частот (длин волн) за время
– энергия, излучаемая (или поглощаемая) телом во всем диапазоне частот (длин волн) за время  .
.
· Энергетическая светимость тела:

где  – поток излучения с участка поверхности тела площадью
– поток излучения с участка поверхности тела площадью  .
.
· Закон Стефана-Больцмана
 ,
,
где  – энергетическая светимость (излучательность) чёрного тела;
– энергетическая светимость (излучательность) чёрного тела;  – постоянная Стефана-Больцмана;
– постоянная Стефана-Больцмана;  – абсолютная температура.
– абсолютная температура.
· Энергетическая светимость серого тела
 ,
,
где  – поглощательная способность серого тела.
– поглощательная способность серого тела.
· Спектральная плотность энергетической светимости
 .
.
· Связь энергетической светимости и спектральной плотности энергетической светимости чёрного тела
 .
.
· Закон смещения Вина

где 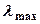 – длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости чёрного тела;
– длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости чёрного тела;  – постоянная Вина.
– постоянная Вина.
· Зависимость максимальной спектральной плотности энергетической светимости чёрного тела от температуры

где 
· Формула Рэлея-Джинса для спектральной плотности энергетической светимости чёрного тела

где  – постоянная Больцмана;
– постоянная Больцмана;
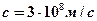 – скорость света в вакууме;
– скорость света в вакууме;  – частота излучения.
– частота излучения.
· Энергия кванта света (фотона)

где  - постоянная Планка.
- постоянная Планка.
· Импульс и масса фотона
 ,
,  .
.
· Формула Эйнштейна для внешнего фотоэффекта
 ,
,
где  – работа выхода электрона из металла;
– работа выхода электрона из металла;  – максимальная кинетическая энергия фотоэлектрона,
– максимальная кинетическая энергия фотоэлектрона,  – масса электрона.
– масса электрона.
Если  , то
, то  или
или  , где
, где  – «красная граница» фотоэффекта, т.е. минимальная частота или максимальная длина волны, при которой возможен фотоэффект.
– «красная граница» фотоэффекта, т.е. минимальная частота или максимальная длина волны, при которой возможен фотоэффект.
· Связь между максимальной кинетической энергией электрона и задерживающим напряжением
 ,
,
где  – заряд электрона.
– заряд электрона.
· Давление света при нормальном падении на поверхность
 ,
,
где  – коэффициент отражения (для зеркальной поверхности
– коэффициент отражения (для зеркальной поверхности  , для чёрной поверхности
, для чёрной поверхности 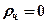 );
);  – объёмная плотность энергии излучения;
– объёмная плотность энергии излучения; 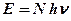 – энергия всех фотонов;
– энергия всех фотонов;  – площадь поверхности, на которую падает свет;
– площадь поверхности, на которую падает свет;  – скорость света в вакууме;
– скорость света в вакууме;  – время воздействия света;
– время воздействия света; 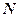 – число фотонов;
– число фотонов;  - объем.
- объем.
· Изменение длины волны рентгеновского излучения при комптоновском рассеянии
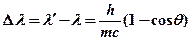 ,
,
где  и
и 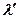 – длина волны падающего и рассеянного излучения соответственно,
– длина волны падающего и рассеянного излучения соответственно,  – масса электрона,
– масса электрона,  – угол рассеяния.
– угол рассеяния.
Задания






