1. Определить и записать в табл. 4.1 отрезки пути l, пройденные шариком за соответствующие промежутки времени.
2. Вычислить скорость шарика u = l/t изаписать в таблицу.
3. Для каждого из шести измерений вычислить вязкость глицерина по формуле (4.8), записать в табл. 4.1.
Примечание: рекомендуем вначале вычислить постоянный множитель C = g (r1 – r2) / 18 в единицах СИ.Плотность шариков и глицерина соответственно: 7800 кг/м3 и1200 кг/м3. Ускорение свободного падения – по табл. П.1 приложения 2.
4. Выполните статистическую обработку результатов измерений по всем значениям h.
5. По среднему значению <h> вычислите коэффициент кинематической вязкости глицерина и значения критерия Рейнольдса для каждого шарика.
6. Сравнить полученное значение коэффициента вязкости с табличным значением для глицерина, выявить возможные причины несоответствия.
Контрольные вопросы
1. Дайте определения: силы сопротивления, силы Архимеда, ламинарного и турбулентного течения. Письменный ответ на этот вопрос необходимо включить в отчет.
2. Каковы цели лабораторной работы и что нужно сделать для их достижения?
3. Назовите составные части лабораторной установки и их назначение.
4. Какие величины измеряются в данной работе непосредственно? Какие вычисляются?
5. Определите размерности коэффициентов динамической и кинематической вязкости. Как называются единицы их измерения в системах СИ и СГС?
6. От каких величин зависит сила сопротивления движению тела в жидкости? Какова зависимость силы сопротивления от скорости для случаев медленного и быстрого движений?
7. Какая физическая величина называется градиентом скорости? Каковы его физический смысл и размерность?
8. Какой критерий подобия определяет характер течения? Запишите его формулу, проверьте размерность.
9. Какие силы действуют на шарик, падающий в жидкости? Опишите характер движения тяжёлого шарика, опущенного без начальной скорости в жидкость.
10. Как коэффициенты вязкости жидкостей зависят от температуры?
11. Выведите формулу (4.5) и расчётную формулу (4.9).
12. Изобразите в виде графика зависимость скорости шарика от времени при начальной скорости u0 = 0.
Цикл 2. Электричество и магнетизм
Содержит описания 4-х лабораторных работ, выполняемых в лаборатории электричества и магнетизма.
Работа № 5. ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель работы: познакомиться с одним из методов моделирования электрических полей, практически определить характеристики поля в плоском и цилиндрическом конденсаторах, построить картину этих полей.
Оборудование: лабораторный стенд; модуль «Электростатика», модуль питания 1,2…12 В, модуль «Наборное поле», мультиметр, соединительные провода.
Краткая теория
При подготовке к работе следует изучить характеристики электрического поля: напряжённость 
и потенциал j,их физический смысл, единицы измерения, методы определения, связь между напряжённостью и потенциалом, теорему Остроградского – Гаусса и её применение для вычисления напряжённости, зависимость и j от координат для различных полей (точечный заряд, нить, цилиндр, плоскость), силовые линии и эквипотенциальные поверхности.
Для изучения полей используют экспериментальные методы их моделирования. Один из них основан на применении слабо проводящего электропроводного материала с прижатыми к ней металлическими электродами. Электростатическое поле заменяют электрическим полем, в котором на электроды подают такие же потенциалы, как и в моделируемом поле. Несмотря на движение заряженных частиц, плотность зарядов на электродах постоянна, так как на место зарядов, уходящих по слабопроводящему материалу, непрерывно поступают новые заряды от источника питания. Поэтому заряды электродов создают на электропроводном материале такое же электрическое поле, как и неподвижные заряды такой же плотности, а электроды являются эквипотенциальными поверхностями. Моделирование на электропроводной бумаге позволяет использовать токоизмерительные приборы, которые более просты и надёжны в работе, чем электростатические.
 |
Картина электростатического поля может быть наглядно представлена линиями напряжённости (сплошные) и эквипотенциальными поверхностями (штриховые) (рис. 5.1 и 5.2).
Линии напряжённости начинаются на положительных зарядах, а заканчиваются на отрицательных, или в бесконечности. Густота линий пропорциональна величине напряжённости. Направление вектора в некоторой точке поля определяют по направлению касательной к силовой линии в этой точке.
Эквипотенциальные поверхности – это поверхности равного потенциала. Они перпендикулярны линиям напряжённости, что следует из равенства нулю элементарной работы d А = – qd j, совершаемой силой 
при бесконечно малом перемещении 
заряда. Если перемещение происходит по эквипотенциальной поверхности, то d j = 0; d А = qEdl cosa = 0, следовательно, угол a между векторами и равен 90° (см. рис. 5.1).
В плоских моделях каждая эквипотенциальная поверхность заменяется линией, во всех точках которой потенциал имеет одно и то же значение. В случае однородного поля уравнение эквипотенциальной линии имеет вид j(x,y)= const. Эквипотенциальные линии строят с постоянным шагом ∆j,т.е. так, чтобы разность потенциалов между двумя соседними линиями была одинаковой: (j0 – j1) = (j1 – j2) = (j2 – j3) = const (рис. 5.2). По густоте эквипотенциальных линий также можно судить о величине напряжённости поля.
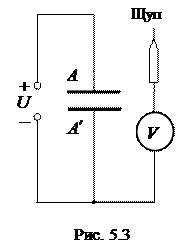В данной работе электрическое поле создается между электродами, прижатыми к электропроводному материалу. Форма электродов в плане соответствует форме двух типов конденсаторов: плоского и цилиндрического. К электродам подводят небольшое постоянное напряжениеот модуля питания (рис. 5.3).
По электропроводному материалу между электродами протекает очень слабый электрический ток, и распределение потенциала по плоскости материала весьма напоминает распределение потенциала между обкладками конденсатора, каждая из которых имеет одинаковый потенциал во всех точках. Известно, что напряжённость электростатического поля и его потенциал j связаны между собой:
 ,
| (5.1) |
где вектор
 .
| (5.2) |
Знак минус является выражением того, что вектор напряжённости электростатического поля направлен против того направления, в котором потенциал увеличивается. Из выражений (5.1) и (5.2) следует, что проекции вектора на оси координат равны частным производным от потенциала по соответствующим координатам, взятым с обратным знаком:
 .
| (5.3) |
Если потенциал зависит только от одной координаты r (поле точечного заряда, равномерно заряженной нити, цилиндра и др.), то проекция Еr вектора напряжённости равна минус производной от потенциала только по координате r:
 ,
| (5.4) |
поскольку производные по другим координатам равны нулю.
Так же и в однородном поле: если направить координату х параллельно силовым линиям, то проекция вектора напряжённости
 .
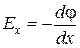| (5.5) |
Измеряя потенциал в различных точках электропроводного материала, и используя связь между напряжённостью и потенциалом электрического поля, можно найти напряжённость как функцию координаты.
В теории напряжённость электростатического поля легко определяется с помощью теоремы Остроградского – Гаусса, а по напряжённости затем вычисляется потенциал или разность потенциалов:
 ;  .
| (5.6) |
Практически же наоборот: напряжённость удобней определять по измеряемому потенциалу j, так как непосредственное измерение напряжённости электрического поля чрезвычайно затруднено.
Разность потенциалов между любыми точками поля можно измерить вольтметром. В данной работе она измеряется между одним из электродов конденсатора и той точкой поля, в которую вставляется щуп мультиметра (см. рис. 5.3–5.5).
В плоском конденсаторе заряды, распределённые на пластинах с поверхностной плотностью s, создают однородное электрическое поле с напряжённостью
 .
| (5.7) |
Так как = const, то в формуле (5.6) проекцию Еr = Ex можно вынести за знак интеграла. Считая потенциал отрицательного электрода 
равным нулю и направляя координату х от этого электрода к положительной пластине A (рис. 5.4),получим линейную зависимость потенциала j от координаты x, направленной против силовых линий:
| j = Ex. | (5.8) |
Измеряя потенциал на различных расстояниях x от пластины 
, и строя график зависимости j (x), мы можем найти напряжённость как угловой коэффициент этого графика. Затем по напряжённости можно найти поверхностную плотность зарядов на пластинах конденсатора из формулы (5.7).
В цилиндрическом конденсаторе напряжённость поля между двумя заряженными длинными соосными цилиндрами можно найти, используя теорему Гаусса. В этом случае зависимость напряжённости Еr от расстояния r до оси цилиндров (рис. 5.5) получается обратно пропорциональная:
 ,
| (5.9) |
где t – линейная плотность зарядов на внутреннем цилиндре. Если он заряжен отрицательно (t < 0), то вектор направлен против координаты r, и проекция Еr также < 0.
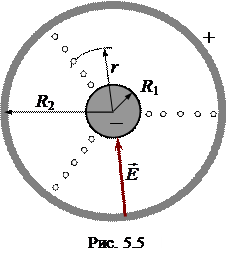Используя выражения (5.6) и (5.9), и полагая потенциал внутреннего цилиндра Б¢ равным нулю, можно показать, что потенциал точки поля, находящейся на расстоянии r от центра конденсатора (см. рис. 5.5), определяется выражением
| (5.10) |
где R1 – радиус внутреннего цилиндра.
Измеряя потенциал на различных расстояниях r от оси цилиндров и строя график зависимости j(r), мы можем найти напряжённость Е в любой точке поля методом графического дифференцирования (так как E = |d j /dr|).
Выполнение работы
 |
1. Соберите схему для изучения электростатического поля плоского конденсатора (рис. 5.3), используя монтажную схему установки (рис. 5.6).
Найдите на модуле «Наборное поле» любые три соединённые вместе гнезда и соедините с ними нулевые контакты (^)мультиметра, модуля питания и пластину конденсатора А ¢ (гнездо А ¢). Плюс источника питания соедините с пластиной А.
2. Регулятор питания 1,2…12 В установите в крайнее левое положение.
3. Переключатель мультиметра установите на «20 В» постоянного напряжения.
4. Покажите собранную схему руководителю работ.
5. Включите модуль питания и мультиметр (красная кнопка слева).
6. Соедините щуп с верхней пластиной А и установите регулятором питания напряжение между электродами в пределах 2…6 В (по показаниям мультиметра).
7. Измерьте потенциалы на обкладках конденсатора, коснувшись щупом нижней и верхней пластин, запишите эти значения в табл. 5.1.
 |
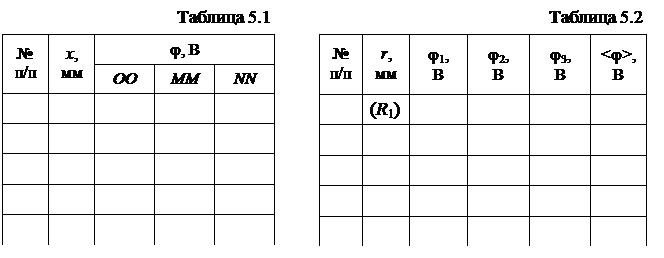8. Измерьте потенциалы в точках поля конденсатора при трёх положениях линейки: ММ, ОО, NN (рис. 5.4). Линейка должна быть из непроводящего материала! Измерения необходимо проводить через каждые 4–5 мм, начиная от внутреннего края нижней пластины. Результаты записывайте в табл. 5.1.
9. Измерьте диаметр центрального электрода цилиндрического конденсатора и запишите его значение в черновик.
10. Поочередно перенесите провода с контакта «А» на контакт «Б» и с контакта А' на Б'. Этим самым Вы перекинете напряжение с плоского конденсатора на цилиндрический. На центральном электроде во всех его точках будет нулевой потенциал, а на внешней обкладке – максимальный. Проверьте, так ли это!
9. Измерения потенциала j проводите от центра конденсатора к внешнему кольцу через каждые 4–5 мм по трём любым радиусам (см. рис. 5.5), начиная от оси центрального электрода. Измеренные значения записывайте в табл. 5.2.
10. По окончании измерений представьте результаты преподавателю (руководителю работ в лаборатории) для проверки и подписи.
11. Выключите модуль питания и мультиметр, разберите схему, наведите порядок на рабочем месте.
