Сопротивления металла и энергии активации полупроводника

 

Цель работы: изучить зависимость сопротивления металлов и полупроводников от температуры, измерить сопротивления металлического проводника и терморезистора при разных температурах, определить температурный коэффициент сопротивления (ТКС) металлического образца и энергию активации полупроводника.

Оборудование: лабораторный стенд; миниблоки «Ключ», «ТКС», мультиметр, стрелочный вольтметр, датчик температуры, модуль питания 1,2…12 В, соединительные провода.

Теория метода

Все вещества по электрическим свойствам разделяют на три класса: проводники, диэлектрики и полупроводники. К проводникам относятся металлы, обладающие малым удельным сопротивлением – менее 10^–6 Ом×м. Удельное сопротивление полупроводников обычно лежит в пределах 10⁵...10¹⁴ Ом×м. Материалы, у которых ве­личина удельного сопротивления больше 10¹⁴ Ом×м, считаются диэлектриками. Полупровод­никами являются некоторые элементы III–VI групп таблицы элементов Д.И. Менделеева (В, Ge, Si, As, Те...), а также большое число хи­мических соединений (GaAs, GaP, ZnS, SiC …). В зависимости от внешних условий (температуры, давления) одно и то же вещество может проявлять разные электрические свойства. Например, германий при темпера­туре жидкого азота 77 К – диэлектрик, при комнатной температуре – полупроводник, а в жидком виде – проводник.

Теория даёт более обоснованную классификацию веществ. Согласно современной зонной теории твёрдых тел свободные электроны внутри твёрдого тела так же, как и в атомах, могут иметь только некоторые фиксированные значения энергии, т.е. энергия электронов квантуется, разрешённыеуровни энергии при объединении атомов в кристалл образуют совокупность близко расположенных уровней – разрешённые зоны, разделённые «запрещёнными» зонами. Каждая разрешённая зона сохраняет наименование уровней, из которых она образована, например, зоны 1 s, 2 s, 2 p и так далее.

Зона, образованная из энергетических уровней самых удалённых от ядра атома валентных электронов, называется валентной зоной. Это самая «верхняя» из зон, заселённых электронами при температуре Т = 0 К (–273 °С). Следующая разрешённая энергетическая зона называется в полупроводниках зоной проводимости. При Т = 0 в этой зоне нет электронов, она «пустая». Энергетические зоны валентных электронов для металлов, диэлектриков и полупроводников и их заполнение при температуре Т = 0 представлены на рис. 6.1. Клеточками и серой заливкой обозначены занятые уровни энергии. Горизонтальные линии – свободные от электронов разрешённые уровни энергии.

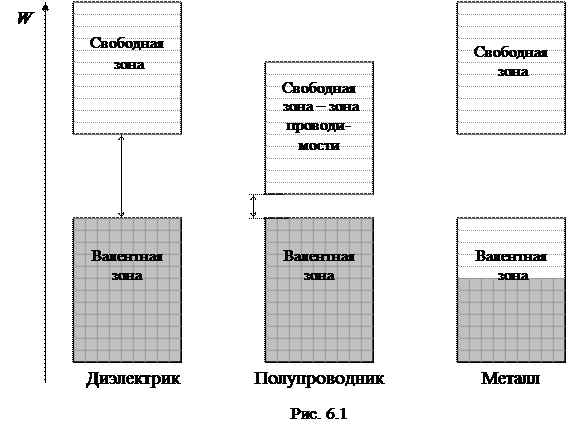
Верхние разрешённые зоны разных веществ могут быть заполнены электронами частично или полностью, а также могут быть совершенно свободными от электронов.

Энергетическая зона считается за­полненной, если все уровни зоны заняты электронами. Такими являются валентные зоны полупроводников и диэлектриков при абсолютном нуле температуры (см. рис. 6.1). При этом, согласно принципу Паули, на одном энергетическом уровне может находиться не более двух электронов, имеющих противоположно направленные спины.

У металлов при Т = 0 валентнаязона заполнена частично(см. рис. 6.1). Например, в кристалле щелочного металла натрия ₁₁Naв валентной зоне 3 s электронами заполнена только половина уровней.

Ширина запрещённой зоны между зоной проводимости и валентной зоной при абсолютном нуле температуры называется энергией активации D W полупроводника (см. рис. 6.1). Энергия активации численно равна работе, которую необходимо совершить электрону при его переходе из валентной зоны в зону проводимости. Энергия активации измеряется в электрон-вольтах (эВ) и составляет у полупроводников 0,1…2 эВ, у диэлектриков больше 4 эВ.

Чтобы в веществе при наложении электрического поля возник электрический ток, электроны должны начать двигаться направленно. Возникновение тока сопровождается увеличением энергии каждого электрона (к энергии теплового движения добавляется энергия направленного движения). В металлах свободный электрон, получив за счет электрического поля дополнительную энергию на пути свободного пробега, переходит на более высокий уровень энергии в валентной зоне. Освободившийся уровень занимает электрон, расположенный ниже на «энергетической лестнице», и т.д. – возникает электрический ток.

В диэлектриках и полупроводниках электрон не может взять энергию от поля, поскольку, приняв её, он должен занять более высокий уровень, который оказывается либо запрещённым, либо занятым. Поэтому при абсолютном нуле и полупроводники, и диэлектрики являются изоляторами, т.е. не пропускают электрический ток.

При повышении температуры энергия теплового движения электронов увели­чивается (их средняя энергия теплового движения < e > = 1,5 kT), и уже при темпе­ратурах порядка 10² К некоторые электроны в полупроводниках за счет этой энергии могут перейти с верхних уровней заполненной валентнойзоны в зону прово­димости (рис. 6.2). В диэлектриках вероятность такого перехода очень мала, так как у них ширина запрещённой зоны значительно больше, чем у полупроводников. Следовательно, в полупроводниках те валентные электроны, которые перешли в зону проводимости, получают возмож­ность направленного движения под дей­ствием электрического поля – возникает электронная проводимость. В валент­ной зоне на верхних уровнях, где были электроны, перешедшие в зону проводи­мости, появляются свободные места – дырки, и оставшиеся в валентной зоне электроны тоже получают способность воспринимать энергию направленного движения от электрического поля – воз­никает дырочная проводимость.

В соответствии с распределением Больцмана концентрация n_e свободных электронов (перешедших в зону проводимости) меньше концентрации n ₀ электронов, оставшихся в валентной зоне, поскольку потенциальная энергия свободных электронов на Δ W больше потенциальной энергии электронов, связанных с атомом:

.

(6.1)

Здесь Т – абсолютная температура; k = 1,38×10^–23 – постоянная Больцмана.

В рассмотренном нами полупроводнике концентрация подвижных дырок равна концентрации свободных электронов. Такой полупроводник называется электронно-дырочным, а его проводимость – собственной проводимостью. Собственной проводимостью обладают очень чистые элементы 4-й группы таблицы Менделеева (германий, кремний).

При наличии в германии или кремнии небольшого количества атомов примесей с другой валентностью баланс между концентрацией свободных электронов и дырок нарушается, и образуются полупроводники с преимущественным типом проводимости. Так, если примесью является элемент 5-й группы таблицы Менделеева (сурьма – Sb, мышьяк – As), то образуется избыток свободных электронов и получается полупроводник с электронной проводимостью (n -типа). Если в качестве примеси присутствуют атомы 3-й группы (индий – In, бор – B), то образуется недостаток свободных электронов и получается полупроводник с дырочной проводимостью (р -типа). Энергия активации примесных полупроводников значительно меньше ширины запрещённой зоны чистого полупроводника.

При отрыве электрона в атоме полупроводника образуется свободное место – дырка. Если теперь в полупроводнике создать электрическое поле, то дырка может переместиться в направлении силовых линий, если это свободное место займёт дрейфующий против поля электрон. Поэтому дырка подобна положительному заряду, равному по величине заряду электрона. Значит при затрате энергии Δ W образуются два свободных заряда, на создание одного носителя тока затрачивается половина энергии Δ W, и концентрация всех носителей тока

.

(6.2)

От концентрации свободных зарядов зависит удельная проводимость σ, обратная удельному сопротивлению r:

.

(6.3)

Зависимость удельной проводимости s от концентрации п свободных зарядов легко получить, используя закон Ома для участка цепи:

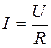
(6.4)

и зависимость сопротивления R проводника от его длины l и площади S поперечного сечения:

.

(6.5)

Полагая электрическое поле внутри проводника однородным, выразим напряжение U через напряжённость Е и длину проводника:

U = El.

(6.6)

Из формул (6.3)–(6.5) легко получить закон Ома в дифференциальной форме:

j = s E,

(6.7)

где j = I/S — плотность тока в проводнике.

С другой стороны плотность тока может быть выражена через концентрацию n свободных зарядов и скорость u_н их направленного движения, которая определяется напряжённостью электрическогополя внутри проводника. Пусть каждый носитель имеет заряд e, тогда весь заряд q, перенесённый через поперечное сечение проводника за время t, будет равен Ne, где N – число зарядов, прошедших за это время сквозь выделенное сечение S (рис. 6.3).

Если средняя скорость направленного движения равна u_н, то за время t сечение S пересекут лишь те носители, которые находились не дальше, чем на расстоянии u_н t от него. Число таких носителей пропорционально их концентрации n и объёму элемента проводника:

N = n uн tS.

(6.8)

Тогда перенесённый заряд

q = en uн tS.

(6.9)

По определению, сила неизменяющегося тока

.

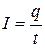(6.10)

Из определения плотности тока и уравнений (6.9) и (6.10) получим

j = ne uн.

(6.11)

Приравнивая правые части уравнений (6.7) и (6.11) приходим к выводу, что средняя скорость направленного движения носителей тока прямо пропорциональна напряжённости электрического поля:

uн = bE.

(6.12)

Коэффициент пропорциональности b называют подвижностью носителей. Подвижность зависит от типа носителей (у электронов она существенно выше, чем у дырок) и от их взаимодействия с атомами вещества.

Заменяя в (6.11) скорость по формуле (6.12) и сравнивая полученное выражение с (6.7), получаем зависимость удельной проводимости вещества от характеристик носителей тока:

s = neb.

(6.13)

В металлах (проводниках) концентрация носителей не зависит от температуры, а в полупроводниках и диэлектриках она с ростом температуры быстро увеличивается (см. формулу (6.2)) – это основное отличие металлических проводников от полупроводников и диэлектриков.

Подвижность носителей с ростом температуры уменьшается, так как электроны чаще сталкиваются с ионами кристаллической решётки, амплитуда колебаний которых растёт с увеличением температуры. При постоянстве п это ведёт к уменьшению проводимости, и сопротивление металлов слабо увеличивается при повышении температуры:

R = R 0(l + αt),

(6.14)

где t – температура в градусах Цельсия; R ₀ – сопротивление проводника при 0 °С; α – температурный коэффициент сопротивления (ТКС).

График зависимости сопротивления проводника от температуры изображается прямой линией, угловой коэффициент которой равен R ₀ α. Определив из графика угловой коэффициент К ₁и R ₀, можно определить значение ТКС исследуемого проводника:

.

(6.15)

У полупроводников зависимость сопротивления от температуры экспоненциальная:

.

(6.16)

Эта формула получается путём несложных преобразований из выражений (6.3), (6.5), (6.13) и (6.2) с заменой l/(Sn ₀ eb) = R ₀, где n ₀ – концентрация носителей тока в полупроводнике при температуре Т ® ¥.

Прологарифмируем формулу (6.16):

ln R = ln R 0 + .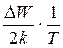

(6.17)

Полученная зависимость ln R от 1/ T является линейной, и график зависимости ln R от обратной температуры T ^–1 будет представлять собой некоторую прямую, угловой коэффициент которой К ₂ = D W/ (2 k) пропорционален энергии активации.Следовательно, найдя из графика угловой коэффициент К ₂, можно вычислить энергию активации

D W = 2 К 2 k.

(6.18)

Выполнение работы

1. Соберите принципиальную схему установки (рис. 6.4) по монтажной схеме (рис. 6.5). Для этого найдите на наборном поле гнёзда для установки миниблоков «Ключ» и «ТКС» (обозначены пунктиром) и аккуратно вставьте в них миниблоки.

Соблюдайте правильность расположения номеров контактов (в гнездо 1 должен попасть 1-й контакт миниблока, во 2-е – 2-й контакт и т.д.). В качестве измерителя сопротивлений используйте мультиметр: выносные гнёзда V/W и COM, предел измерений – «W200». Для установки и контроля напряжения используйте стрелочный вольтметр. При сборке схемы соблюдайте правильную полярность приборов, она указана на схеме.

2. Вставьте в отверстие миниблока «ТКС» датчик температуры на глубину 5–8 мм (до упора) и покажите собранную схему преподавателю.

3. Замерьте сопротивления проводника и полупроводника при комнатной температуре. При положении «Ключа» – «влево» к омметру подключается полупроводник, «вправо» – металлический проводник. Полученные значения запишите в первую строку табл. 6.1.

Таблица 6.1
№ п/п	Т, °С	R, Ом
полупроводник (R пп)	проводник (R п)
…

4. Включите модуль питания. Установите ручкой регулировки на блоке питания напряжение 8–9 В. Температура образцов начнёт увеличиваться. Наблюдайте за показаниями термометра и омметра, переключая тумблер «Ключ». Пока образец нагревается, запишите в табл. 6.1 ряд увеличивающихся значений температуры с шагом 4…5 °С, начиная с температуры 25 °С. Продолжайте нагревание до температуры 65–67 °С. Показания омметра при этом записывать не надо, потому что основные измерения будут проводиться при охлаждении резисторов. Такой способ проведения измерений позволяет исключить влияние блока питания на показания мультиметра, и получить более точные значения сопротивлений проводника R _п и полупроводника R _пп.

5. Выключите блок питания – температура вскоре начнёт уменьшаться. Начиная с 65 °С, считывайте с дисплея мультиметра и записывайте одновременно (переключая тумблер «Ключ») значения сопротивлений проводника и полупроводника в табл. 6.1 при температурах, записанных в таблицу при нагревании.

7. По окончанию работы выключите модуль питания, мультиметр и покажите результаты измерений преподавателю. Разберите схему, сдайте миниблоки и набор проводов, наведите порядок на рабочем месте.