Содержание.
Высшая математика, статистика. (I)
Дифференциал.
Интеграл
Дифференциальные уравнения.
Введение в статистику
Дискретные случайные величины
Непрерывные случайные величины
Основы выборочного метода
Оценка погрешностей измерений
Проверка нулевой гипотезы
Корреляционный анализ
Регрессионный анализ
Физика жидкостей (II)
1. Коэффициент поверхностного натяжения жидкости
Коэффициента вязкости жидкости (метод Стокса)
3. Измерение вязкости жидкости (медицинский вискозиметр)
4. Коэффициента вязкости жидкости (вискозиметр Освальда)
Изучение природы неньютоновских жидкостей
Акустика, оптика (III)
Снятие кривой порога слышимости
Изучение дифракции (изображение в микроскопе)
Концентрация цветного раствора (фотоэлемент)
Концентрация сахара в растворе (поляриметр)
Показатель преломления жидкости (рефрактометр)
Медицинская электроника (IY)
Изучение электронного осциллографа
Измерение импеданса живых тканей
Электротерапия. (Аппарат ИНТЕРДИН)
Аппарат УВЧ терапии
Изучение поля электрического диполя
Электрокардиограф и формирование ЭКГ
Основы усилительной техники
Биофизика клетки. (Y)
Измерение потенциала покоя нервных клеток в виртуальном компьютерном эксперименте.
Дополнительные работы (YI)
Измерение модуля Юнга костной ткани
Изучение механических моделей тканей
Полупроводниковый терморезистор
Взвешивание на аналитических весах
Определение увеличения микроскопа
Измерение влажности воздуха
Градуировка термопары
Тепловое излучение нагретых тел
Активность радиоактивного препарата
Фармакологическая модель
Основы рентгенологии.
Молекулярная физика и термодинамика
Потенциал действия. Измерения характеристики
Возбуждения в виртуальном опыте.
Задания по практическим навыкам
к лабораторно практическому курсу Медицинской физики
Высшая математика, статистика. (I)
Дифференциал.
| Понятие производной Y'(x) от функции Y(x). позволяет указать, ……………………. ………………………………………… Если производная Y'(x) принимает большое значение (вблизи какой либо точки), - то …………………………………… | |
| Производная определяется через предел Y' = Lim (ΔY / ΔX), при Δ X стремящимся к нулю. Прочитайте формулу………………………………………….. | |
| Укажите последовательность действий для вычисления производной "по определению" (для функции Y=x2)……………… | |
| Основные элементарные функции и написать для них производные………………………. | |
| (U + V) ' = U' + V'; (U - V)' = U' - V'; (U * V)' = U' * V + U * V'; (U / V)' = (U' * V - U * V') / V 2. | |
| Дифференциал функции dY = Y’ * Δx = Y’ *dx. | |
| Сложной функцией называют функцию не от независимого аргумента х, а функцию от некоторой другой функции. | |
| Производная сложной функции равна произведению производных от каждой функции: Y' = Y'U(x) * U'x. Y'U(x) - это производная внешней функции, U'x – производная внутренней функции.. | |
| Для приближенного вычисления значения функции в некоторой точке приращение функции можно заменить дифференциалом функции: Y(Xo + ΔX) ≈ Y(Xo) + Y'(Xo) * ΔX. Это формула будет тем точнее, чем меньше приращение аргумента. | |
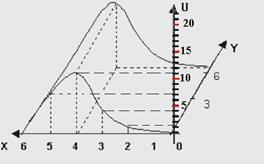
| Многие величины зависят не от одной, а сразу от нескольких величин. Так сила тока по закону Ома зависит и от напряжения, и от сопротивления: I = U / R. (запись I = I(U,R)) В общем случае приняты обозначения U = U(X,Y,Z). Такая запись и отражает тот факт, что величина U является функцией сразу трех независимых переменных - X,Y,Z. | |
| Частные производные находят по тем же правилам, что и производные для функции одной переменной. Если берут производную по аргументу "x", на другие переменные - y и z смотрят как на постоянные числа! Например, U = x + xy2 - xyz4. Тогда U'x = 1 + y2 - yz4, U'y = 0 + x(2y) - xz4, U'z = xy4z3… | |
| Частный дифференциал, например, по переменной Х это произведение частной производной по этой переменной на приращение этой же переменной: dUx = U'x * Δ x. (аналогично для других переменных) Полный дифференциал это сумма частных дифференциалов: dU = dUx + dUy + dUz. | |
| Графически функции двух переменных отображается поверхностью. Каждой паре значений Х и У соответствует одно значение U. Если фиксировать значение У, то можно получить срез – плоскость ХОU. Частной производной по аргументу Х будет соответствовать тангенс угла наклона касательной ОА. Если фиксировать значение X, то можно получить срез – плоскость УОU. | |
| 
|
Указать внешнюю и внутреннюю функцию…
Интеграл
Если вы знаете, что производная от функции y = Sin(x) есть функция Y' = Cos(x), то вопрос о понятии первообразной - вопрос лишь терминологии.
В нашем примере
· функция косинуса является производной для функции синуса,
· функция же синуса является (называется) ПЕРВООБРАЗНОЙ по отношению к функции косинуса.
Итак, функция F(x) называется первообразной для f(x), если
F ' (x) = f(x).
Неопределенным интегралом от функции f(x) называется множество всех ее первообразных. Принято записывать
∫ f(x)dx = F(x) + C
Таблица неопределенных интегралов в силу определения первообразной функции вытекает непосредственно из таблицы производных.
Аналогично объясняются другие табличные интегралы.
Так, например, если (х3)' = 3x2,
то ∫ 3x2dx = x3 + C или ∫ x2dx = x3 / 3 + C.
Сущность любого метода интегрирования состоит в сведении заданного интеграла к табличному виду.
Метод замены переменной можно применить, если в подынтегральном выражении встречается сложная функция. Приведем пример: пусть требуется найти интеграл ∫ Sin4x* Cosx*dx. Видим, что здесь имеется сложная функция Sin4x - степенная от тригонометрической. Решение проведем в несколько этапов:
1. Обозначим за новую переменную внутреннюю функция
Z = Sinx.
2. Теперь следует найти дифференциал новой переменной
dZ = Z' * dx = Cosx * dx,
3. Выразим дифференциал старой переменной
dx = dZ/Cosx,
4. Подставим все в исходный интеграл:
∫ z4* Cosx*dz/Cosx.
Cosx - сократились, и получился табличный интеграл
∫ z4* dz = z5/5 +C.
| ………………………… ………………………… ………………………… ………………………… ………………………… ………………………… ………………………… ………………………… | 
|
| 
|
Понятие определенного интеграла.
∫bf(x)dx = Lim{Σ f(d)*dx} при n → ∞.
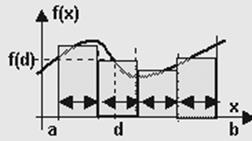число - равное площади под графиком функции f(x) на отрезке ab.
| 
|
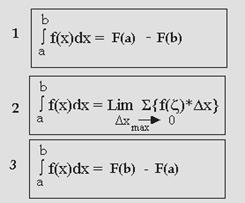
