Теорема. Если 
и 
– линейно независимые решения уравнения (2.3), то их линейная комбинация 
, где 
и 
– произвольные постоянные, будет общим решением этого уравнения.
Доказательство. То, что 
есть решение уравнения (2.3), следует из теоремы о свойствах решений лоду 2-го порядка. Надо только еще показать, что решение будет общим, т.е. надо показать, что при любых начальных условиях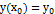 
, 
можно выбрать произвольные постоянные и так, чтобы удовлетворить этим условиям. Запишем начальные условия в виде: 
Постоянные и из этой системы линейных алгебраических уравнений определяются однозначно, так как определитель этой системы 
есть значение определителя Вронского для линейно независимых решений лоду при 
: 
,
а такой определитель, как мы видели в предыдущем параграфе, отличен от нуля. Теорема доказана.
Построение общего решения ЛОДУ II-го порядка с постоянными коэффициентами в случае
13. простых корней характеристического уравнения (случай D>0) (c док-вом).
14. кратных корней характеристического уравнения (случай D=0) (c док-вом).
15. комплексно-сопряженных корней характеристического уравнения (случай D<0) (c док-вом).
Дано лоду 2-го порядка с постоянными коэффициентами 
(5.1), где 
, 
. Согласно предыдущему параграфу общее решение лоду 2-го порядка легко определяется, если известны два линейно независимых частных решения этого уравнения. Простой метод нахождения частных решений уравнения с постоянными коэффициентами предложил Л. Эйлер. Это метод, который называется методом Эйлера, состоит в том, что частные решения ищутся в виде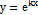 
.
Подставляя эту функцию в уравнение (5.1), после сокращения на 
, получим алгебраическое уравнение, которое называется характеристическим: 
(5.2)
Функция 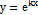будет решением уравнения (5.1) только при тех значениях k, которые являются корнями характеристического уравнения (5.2). В зависимости от величины дискриминанта 
возможны три случая.
1. 
. Тогда корни характеристического уравнения различны: 
. Решения 
и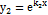 
будут линейно независимыми, т.к. 
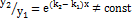и общее решение (5.1) можно записать в виде 
.
2. 
. В этом случае 
и . В качестве второго линейно независимого решения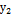 
можно взять функцию 
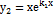. Проверим, что эта функция удовлетворяет уравнению (5.1). Действительно, 
, 
. Подставляя эти выражения в уравнение (5.1), получим
или 
, т.к. 
и 
.
Частные решения 
и 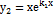линейно независимы, т.к. 
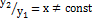. Следовательно, общее решение (5.1) имеет вид:
или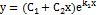 
.
3. 
. В этом случае корни характеристического уравнения комплексно-сопряженны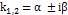е: 
, где 
, 
. Можно проверить, что линейно независимыми решениями уравнения (5.1) будут функции 
и 
. Убедимся, что уравнению (5.1) удовлетворяет, например, функция y1. Действительно, 
, 
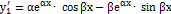. Подставив эти выражения в уравнение (5.1), получим
.
Обе скобки в левой части этого равенства тождественно равны нулю. Действительно, 
,
. Таким образом, функция удовлетворяет уравнению (5.1). Аналогично нетрудно убедиться в том, что и есть решение уравнения (5.1). Поскольку 
, то общее решение будет иметь вид: 
.
16. Теорема о структуре общего решения ЛНДУ II-го порядка (с док-вом).
Теорема 1. Общее решение лнду 2-го порядка 
f(x) (6.1)представляется в виде суммы общего решения 
соответствующего однородного уравнения 
(6.2)и любого частного решения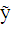 
лнду (6.1).
Доказательство. Докажем сначала, что 
будет решением уравнения (6.1). Для этого подставим в уравнение (6.1): 
f(x). Это равенство является тождеством, т.к. 
и 
f(x). Следовательно, есть решение уравнения (6.1).
Докажем теперь, что это решение является общим, т.е. можно так выбрать входящие в него произвольные постоянные, что будут удовлетворяться любые начальные условия вида: 
, 
(6.3). Согласно теореме о структуре общего решения линейного однородного дифференциального уравнения (лоду) общее решение уравнения (6.2) можно представить в виде 
, где 
и 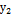– линейно независимые решения этого уравнения. Таким образом: 
и, следовательно, начальные условия (6.3) можно записать в виде: 
или 
(6.4)
Произвольные постоянные и определяются из этой системы линейных алгебраических уравнений однозначно при любых правых частях, т.к. определитель этой системы = 
есть значение определителя Вронского для линейно независимых решений уравнения (6.2) при , а такой определитель, как мы видели выше, отличен от нуля. Определив постоянные и из системы уравнений (6.4) и подставив их в выражение , мы получим частное решение уравнения (6.1), удовлетворяющее заданным начальным условиям. Теорема доказана.
17. Построение частного решения ЛНДУ II-го порядка в случае правой части вида 
Пусть в уравнении (6.1) коэффициенты постоянны, т.е. уравнение имеет вид: 
f(x) (7.1) где 
.
Рассмотрим метод отыскания частного решения 
уравнения (7.1) в случае, когда правая часть f(x) имеет специальный вид. Это метод называется методом неопределенных коэффициентов и состоит в подборе частного решения в зависимости от вида правой части f(x). Рассмотрим правые части следующего вида:
1. f(x) 
, где 
– многочлен степени 
, причем некоторые коэффициенты, кроме 
, могут равняться нулю. Укажем вид, в котором надо брать частное решение в этом случае.
а) Если число 
не является корнем характеристического уравнения для уравнения (5.1), то частное решение записываем в виде: 
, где 
– неопределенные коэффициенты, которые подлежат определению методом неопределенных коэффициентов.
б) Если 
является корнем кратности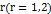 
соответствующего характеристического уравнения, то частное решение ищем в виде: 
, где – неопределенные коэффициенты.
18. f(x) 
, где 
и 
- многочлены степени 
и 
соответственно, причем один из этих многочленов может равняться нулю. Укажем вид частного решения в этом общем случае.
А) Если число 
не является корнем характеристического уравнения для уравнения (5.1), то вид частного решения будет: 
, (7.2) где 
– неопределенные коэффициенты, а 
.
Б) Если число является корнем характеристического уравнения для уравнения (5.1) кратности 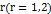, то частное решение лнду будет иметь вид: 
, (7.3) т.е. частное решение вида (7.2) надо умножить на 
. В выражении (7.3) 
- многочлены с неопределенными коэффициентами, причем их степень .
19. Метод вариации для решения ЛНДУ II-го порядка (метод Лагранжа).
Непосредственное нахождение частного решения лнду, кроме случая уравнения с постоянными коэффициентами, причем со специальными свободными членами, представляет большие трудности. Поэтому для нахождения общего решения лнду обычно применяют метод вариации произвольных постоянных, который всегда дает возможность найти общее решение лнду в квадратурах, если известна фундаментальная система решений соответствующего однородного уравнения. Этот метод состоит в следующем.
Согласно вышеизложенному, общее решение линейного однородного уравнения:
, (8.1)
где 
– линейно независимые на некотором интервале X решения лоду, а 
- произвольные постоянные. Будем искать частное решение лнду в форме (8.1), считая, что – не постоянные, а некоторые, пока неизвестные, функции от 
: 
. (8.2) Продифференцируем равенство (8.2): 
. (8.3)
Подберем функции 
и 
так, чтобы выполнялось равенство: 
. Тогда вместо (8.3) будем иметь:
. (8.4)
Продифференцируем это выражение еще раз по . В результате получим: 
. (8.5) Подставим (8.2), (8.4), (8.5) в лнду 2-го порядка 
f(x):
f(x)
Или 
f(x). (8.6)
Так как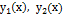 
- решения лоду 
, то последнее равенство (8.6) принимает вид: 
f(x).
Таким образом, функция (8.2) будет решением лнду в том случае, если функции и удовлетворяют системе уравнений:
(8.7)
Так как определителем этой системы является определитель Вронского для двух линейно независимых на X решений соответствующего лоду, то он не обращается в ноль ни в одной точке интервала X. Следовательно, решая систему (8.7), найдем 
и 
: 
и 
. Интегрируя, получи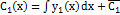 
, 
, где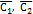 
– произв. пост.
Возвращаясь в равенство (8.2), получим общее решение неоднородного уравнения: 
.
Ряды
1. Числовые ряды. Основные понятия, свойства сходящихся рядов. Необходимый признак сходимости (с док-вом).
Основные определения. Пусть дана бесконечная числовая последовательность 
. Числовым рядом называется составленная из членов этой последовательности запись 
. Или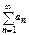 
.Числа 
называют членами ряда;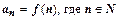 
, называется общим членом ряда. В результате вычисления значений этой функции при n =1, n =2, n =3, … должны получаться члены ряда 
.
Пусть дан ряд (18.1.1). Составим из его членов конечные суммы, называемые частичными суммами ряда: 
Определение. Если существует конечный предел S последовательности частичных сумм ряда (18.1.1) при 
, то говорят, что ряд сходится; число S называют суммой ряда и пишут 
или 
.
Если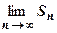 
не существует (в том числе бесконечен), ряд называется расходящимся.
Свойства сходящихся рядов. Необходимый признак сходимости ряда. Общий член сходящегося ряда 
стремится к нулю при : 
Доказательство. Если 
, то и 
, но 
, следовательно 
.
С проверки выполнения условия 
надо начинать решение любой задачи на исследование сходимости ряда: если это условие не выполняется, то ряд заведомо расходится. Это условие необходимо, но не достаточно для сходимости ряда: общий член гармонического ряда (18.1.2) 
, однако этот ряд расходится.
Определение. Остатком ряда после n -го члена называется ряд 
.
Св-во 1. Если сходится ряд, то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.
Доказательство. Пусть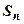 
- частичные суммы ряда (18.2.1); обозначим k -ую частичную сумму остатка 
: 
. Тогда 
. Устремим 
, считая n фиксированным числом. Ряд (18.2.1) сходится, т.е. существует конечный 
, следовательно существует конечный предел 
, т.е. остаток сходится. Обратное утверждение доказывается также. Так как 
, то из существования конечного предела 
следует существование конечного предела , т.е. из сходимости остатка следует сходимость ряда. Т.е. отбрасывание конечного числа начальных членов ряда или добавление в его начало нескольких новых членов не влияет на сходимость ряда.
Св-во 2. Если ряд сходится, то сумма его остатка после n -го члена стремится к нулю при .
Доказательство. Пусть S - сумма исходного ряда (18.2.1), 
- сумма его остатка. Из равенства следует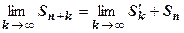 
, т.е. 
. Отсюда 
.
Из предыдущего свойства следует, что сходимость ряда определяется сходимостью его остатка, т.е. хвостом ряда, а сумма S ряда, как следует из равенства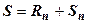 
, о пределяется пределом 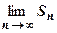, т.е. началом ряда.
Св-во 3. Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.
Доказательство. Частичная сумма ряда 
есть 
; по свойству предела 
.
Св-во 4. Два сходящихся ряда 
и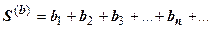 
можно почленно складывать и вычитать; ряд 
также сходится, и его сумма равна 
.
Доказательство и этого свойства - прямое следствие свойств пределов для частичных сумм: 
.
2. Гармонический ряд. Ряды Дирихле.
Сходимость рядов с положительными членами (положительных рядов). Термином "положительный ряд" мы будем называть числовой ряд с неотрицательными членами: 
для 
. Для таких рядов частичная сумма 
является возрастающей функцией аргумента n. Монотонно возрастающая функция имеет конечный предел тогда и только тогда, когда она ограничена сверху, поэтому сразу сформулируем признак сходимости положительных рядов:
