Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида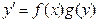 
(3.1) или уравнение вида 
(3.2)
Для того, чтобы в уравнении (3.1) разделить переменные, т.е. привести это уравнение к так называемому уравнению с разделенными переменными, произвести следующие действия: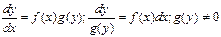 
;
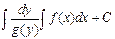Теперь надо решить уравнение g(y)= 0. Если оно имеет вещественное решение y=a, то y=a тоже будет решением уравнения (3.1).
Уравнение (3.2) приводится к уравнению с разделенными переменными делением на произведение 
:
, что позволяет получить общий интеграл уравнения (3.2):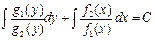 
. (3.3)
Интегральные кривые (3.3) будут дополнены решениями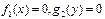 
, если такие решения существуют.
Однородные дифференциальные уравнения 1-го порядка.
Определение 1. Уравнение 1-го порядка 
называется однородным, если для его правой части при любых 
справедливо соотношение 
, называемое условием однородности функции двух переменных нулевого измерения.
Пример 1. Показать, что функция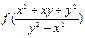 
- однородная нулевого измерения.
Решение.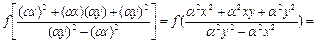 
,
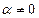что и требовалось доказать.
Теорема. Любая функция 
- однородна и, наоборот, любая однородная функция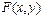 
нулевого измерения приводится к виду 
.
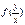Доказательство. Первое утверждение теоремы очевидно, т.к. 
. Докажем второе утверждение. Положим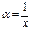 
, тогда для однородной функции 
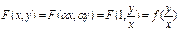, что и требовалось доказать.
Определение 2. Уравнение 
(4.1) в котором M и N – однородные функции одной и той же степени, т.е. обладают свойством 
при всех 
, называется однородным. Очевидно, что это уравнение всегда может быть приведено к виду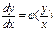 
(4.2), хотя для его решения можно этого и не делать. Однородное уравнение приводится к уравнению с разделяющимися переменными с помощью замены искомой функции y по формуле y=zx, где z(x) – новая искомая функция. Выполнив эту подстановку в уравнении (4.2), получим: 
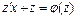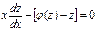или 
или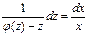 
.
Интегрируя, получаем общий интеграл уравнения относительно функции z(x)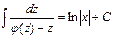 
, который после повторной замены 
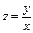дает общий интеграл исходного уравнения. Кроме того, если 
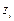- корни уравнения 
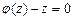, то функции 
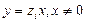- решения однородного заданного уравнения. Если же 
, то уравнение (4.2) принимает вид
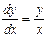и становится уравнением с разделяющимися переменными. Его решениями являются полупрямые: 
.
Замечание. Иногда целесообразно вместо указанной выше подстановки использовать подстановку x=zy.
Обобщенное однородное уравнение.
Уравнение M(x,y)dx+N(x,y)dy=0 называется обобщенным однородным, если удается подобрать такое число k, что левая часть этого уравнения становится однородной функцией некоторой степени m относительно x, y, dx и dy при условии, что x считается величиной первого измерения, y – k‑ го измерения, dx и dy – соответственно нулевого и (k-1) -го измерений. Например, таким будет уравнение 
. (6.1) Действительно при сделанном предположении относительно измерений x, y, dx и dy члены левой части 
и dy будут иметь соответственно измерения -2, 2 k и k -1. Приравнивая их, получаем условие, которому должно удовлетворять искомое число k: -2 = 2 k = k -1. Это условие выполняется при k = -1 (при таком k все члены левой части рассматриваемого уравнения будут иметь измерение -2). Следовательно, уравнение (6.1) является обобщенным однородным.
Обобщенное однородное уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки 
, где z – новая неизвестная функция. Проинтегрируем указанным методом уравнение (6.1). Так как k = -1, то 
, после чего получаем уравнение 
.
Интегрируя его, находим 
, откуда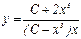 
. Это общее решение уравнения (6.1).
