При рассмотрении равномерного прямолинейного движения допускалось, его скорость во всех точках на участке движения остаётся постоянной по направлению и величине; 
. Однако на участке начала движения скорость изменяется от нуля до необходимого значения, тогда как на участке окончания движения уменьшается до нуля. Не вдаваясь пока в причины неравномерности движения на начальном и конечном участках движения, можно ожидать, должна быть физическая величина, характеризующая быстроту изменения скорости. Количественная математика подсказывает, если мы знаем величину изменения скорости 
и промежуток времени, в течение которого это изменение скорости произошло D t = t 2 – t 1, то быстрота изменения скорости может быть найдена математической операцией деления. Отношение изменения скорости к промежутку времени 
, за которое это изменение произошло, называется ускорением. В символическом представлении ускорение запишется так: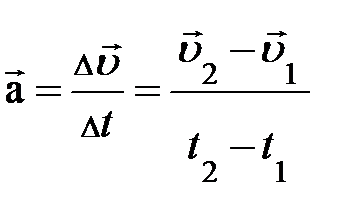 
. Поскольку скорость величина векторная, ускорение также является векторной величиной; кроме численного значения новая физическая величина имеет направление. В частности, в приведённом примере на участке начала движения направление вектора ускорения совпадает с направлением вектора скорости, тогда как на участке прекращения движения – противоположно по направлению вектору скорости (отобразите на рисунке). Из символической записи ускорения следует, оно измеряется в метрах на секунду в квадрате (м/с2).
Основная задача кинематики – определить положение движущегося тела в пространстве в любой момент времени. Для этого необходимо знать закон изменения положения движущегося тела, 
; закон движения. Найдём для равнопеременного движения уравнение, отражающее изменение координаты (положения) тела в пространстве с течением времени.
Символическое представление ускорения 
позволяет записать уравнение скорости как функцию времени: 
. Здесь 
– отображает скорость 
, с которой будет двигаться тело через время t после начала отсчёта; 
– представляет скорость 
с которой двигалось тело в тот момент, когда запустили время отсчёта. Эти пояснения важны, когда кратко записывается «дано» из условия задачи.
Из уравнения скорости следует, для равнопеременного движения скорость является линейной функцией времени. Из алгебры известно, среднее значение линейной функции равно половине суммы её начального и конечного значений на любом временном интервале. В этом случае средняя скорость равнопеременного движения запишется: 
. Это позволяет записать закон изменения положения движущегося тела при равнопеременном движении в виде: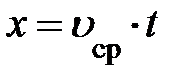 
. Если учесть символическую запись средней скорости, уравнение равнопеременного движения примет вид: 
(самостоятельно преобразования проделали?). Для этого необходимо записать систему из двух уравнений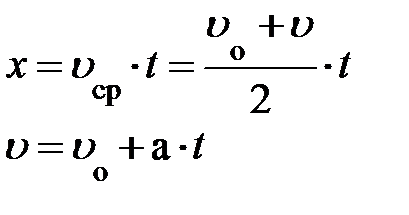 
и преобразовать её. Удачи.
Решение задач равнопеременного движения сложнее. Почему? Во-первых, необходимость в двух уравнениях – координаты и скорости. Во-вторых, чтобы записать уравнения, необходимо сделать чертёж для правильного понимания условия задачи. И, в-третьих, чертёж помогает записать промежуточные математические операции, без которых подчас нельзя определить «скрытый» параметр. Например: С крыши дома высотой 16 метров через равные промежутки времени падают капли воды, причём первая ударяется о землю в тот момент, когда пятая отделяется от крыши. Найти расстояние четвёртой капли от крыши в момент удара первой капли о землю. Если нарисовать чертёж, из него следует, первая капля падала четыре равных промежутка времени. Об этих равных промежутках времени упоминается в условии задачи. Следовательно, четвёртая капля падала в течении одно промежутка времени. Найти время падения первой капли просто: вблизи земли все тела падают с известным ускорением свободного падения; высота падения известна; начальная скорость оговорена словом «отделяется», то есть без … Догадались? Удачи. Кстати, вопрос задачи можно переформулировать: Найти расстояние между четвёртой и первой каплей в момент удара первой капли о землю.
Итак, решение задач равнопеременного движения позволяет приобрести навыки понимания текста, осуществлять поиск заданных физических величин, формировать аналитическую запись происходящего в задаче.
Завершая экскурс в раздел кинематики «равнопеременное движение», перечислим его ключевые слова: скорость, изменение скорости, ускорение, уравнение скорости, уравнение движения.
Вращательное движение
Вращательное движение является частным случаем криволинейного движения. Кроме того, будем рассматривать движение материальной точки по окружности с постоянной по модулю скоростью,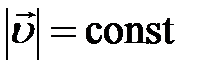 
. Это упрощает строгость аналитического рассмотрения и позволяет удовлетвориться геометрической иллюстрацией.
Пусть точечное тело (материальная точка) движется по окружности радиуса R (рис. 1.3). За некоторый промежуток времени Dt оно пройдёт путь DS, равный дуге АВ. В точке А тело имело скорость , в точке В скорость , а радиус-вектор движущееся точки R повернулся на некоторый угол Dj (рис. 1.3). Изменилось и направление вектора скорости. Если у вектора скорости изменяется хотя бы один параметр – или модуль, или направление, можно говорить о быстроте её изменения, ускорении. Естеств 
| Рис. 1.3. |
. Геометрическая иллюстрация вращательного движения (рис. 3) позволяет эту запись представить следующим образом: 
. Прочитать её можно так: вектор 
, характеризующий изменение скорости по направлению, представляет собой сумму векторов () и (– ) и соединяет начало первого вектора () с концом второго вектора (– ), рис. 1.3. Это позволяет выразить модуль, численное значение вектора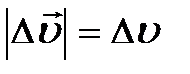 
через кинематические характеристики: скорость и радиус окружности. Действительно, ÐАОВ = ÐВСD как углы с взаимно перпендикулярными сторонами (построением убедились?; можно рассуждениями); по числовому значению скорость постоянна и 
. Следовательно, rАОВ и rВСD подобны по двум сторонам и углу между ними (почему?), отсюда из rВСD следует 
, а из rАОВ этот же угол 
(см. рис. 1.3.). Поскольку левые части уравнений равны (углы с взаимно перпендикулярными сторонами), то из правых частей немедленно следует, модуль, численное значение вектора 
(самостоятельно проделали?). По определению ускорение, в нашем случае характеризующее изменение скорости по направлению, равно 
. Если промежуток времени Dt взять малым, то хорда АВ стремится к длине дуги АВ, или пройденному пути DS за время Dt. Перепишите на листке аналитическое выражение ускорения (а) и самостоятельно замените в нём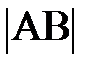 
на пройденный путь DS. Поскольку DS/Dt = 
, для символической записи ускорения, характеризующего быстроту изменения скорости по направлению, получим выражение 
(преобразования проделайте самостоятельно). Направление центростремительного ускорения можно определить по рис. 1.3. Из треугольника скоростей, rВСD следует, чем меньше промежуток времени Dt, тем меньше угол D j. При этом векторы 
и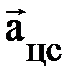 
, имеют одинаковое направление и направлены по радиусу R окружности к её центру O.При рассмотрении равномерного движения по окружности привлекались как линейные кинематические характеристики перемещение, путь, скорость, ускорение, радиус окружности, так и угловая характеристика – угол поворота Dj, опирающийся на отрезок АВ. Появление угла поворота связано с линейными величинами, естественно желание прописать равномерное движение материальной точки по окружности и через угловые характеристики. При вращательном движении угол поворота является основной кинематической характеристикой и с точки зрения количественной математики в общем виде может быть записан следующим образом: Dj = = j2 –.j1 = j2 = j = 2×p×N; если j1 = 0. Прочитаем эту запись: изменение угла поворота Dj равно разности конечного (j2) и начального (j1) значений; если же начальный угол j1 = 0, обозначать конечное значение значком j2 не имеет смысла и цифру два опускают.
Итак, угол поворота j = 2×p×N, естественно, это произошло за время Dt; здесь 2p = 360о и представляет собой один полный оборот, N – число оборотов за время движения; не обязательно полных, например, 0,37. Отношение угла поворота к времени, в течение которого это изменение произошло, будет характеризовать изменение угла поворота в единицу времени, то есть это быстрота изменения угла поворота или угловая скорость w. Аналитически это может быть представлено следующим образом: 
. Поскольку появление угловых характеристик обусловлено наличием линейных, естественно ожидать взаимосвязь между угловой и линейной скоростями. Ранее нам удалось показать, что (рис. 1.3). Если воспользоваться малыми углами, то 
и тогда немедленно следует: 
. Подставляя в аналитическое выражение угловой скорости, получим 
, то есть угловая скорость связана с линейной скоростью выражением 
(преобразования проделали самостоятельно?).
Ещё две характеристики, полезные для технических целей, могут быть введены из уравнения: j = 2p×N = w×t. Действительно, если N = 1, уравнение примет вид: 2p×1 = w×t. Здесь t время одного полного оборота. Его принято обозначать буквой Т – время одного оборота. Тогда 2p = w×Т, отсюда следует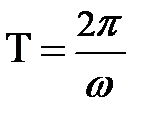 
, а 
. Если известно время одного полного оборота, а единицу времени одну секунду разделить на время одного оборота, получим вторую характеристику движения материальной точки по окружности; или для вращательного движения. Её принято называть частотой вращения 
. Единицей измерения периода является секунда (с); единицей частоты вращения герц (Гц). 1 Гц – частота периодического процесса, при которой за время, равное одной секунде, происходит один цикл периодического процесса.
Для снятия сомнений в понятии «малые углы», проделайте следующие действия: воспользуйтесь тригонометрической таблицей или калькулятором и найдите sin10о. Нашли? Запишите это значение. Проделайте следующие действия: 2p радиан равны 360о; найдите операцией «деление» сколько в одном градусе радиан; нужно 2p разделить на 360о, разделили?; не забыли, что p = 3,14 радиан?; умножьте на 10о. Если уже умножили, сопоставьте с табличным результатом или найденным по калькулятору. В каком знаке ошибка? Вы с такой точностью умеете считать? Можно ли согласиться с понятием «малые углы»? Наверное, всё-таки можно!
В заключение две дежурные задачи. Запишите центростремительное ускорение через угловую скорость; период обращения, частоту вращения. Введение угловых характеристик позволяет записать уравнение движения тела по окружности через угловые характеристики. Как будет выглядеть уравнение движения: j = f(t) через угловую скорость; период вращения; частоту вращения?; это и есть вторая задача.
Завершая экскурс в раздел кинематики «вращательное движение», перечислим его ключевые слова: угол поворота, малый промежуток времени, угловая скорость, центростремительное ускорение, период вращения, частота вращения.
Динамика Ньютона
