ЦЕЛЬ РАБОТЫ
1. Изучение тепловых процессов в идеальном газе.
2. Экспериментальное определение коэффициента Пуассона.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
1. Стеклянный баллон с воздухом.
2. Насос.
3. Водяной манометр.
4. Измерительная линейка.
ВВЕДЕНИЕ
Равновесное состояние термодинамической системы характеризуется совокупностью величин, называемых параметрами состояния. В простейших случаях параметрами состояния являются давление р, объем V и абсолютная температура Т.
Уравнение, устанавливающее связь между р, V, Т, называется уравнением состояния. В явном виде уравнение состояния известно только для некоторых систем. Например, уравнение состояния идеального газа имеет вид
 .
| (1) |
Равновесным состоянием термодинамической системы называется такое состояние, которое не изменяется со временем и неизменность его параметров не обусловлена каким-либо внешним относительно данной системы процессом. Состояние равновесия не означает, что в термодинамической системе нет никакого движения. Например, в газе, который находится в состоянии термодинамического равновесия, молекулы интенсивно движутся. Равновесие термодинамической системы есть равновесие статистическое. Оно характеризуется тем, что мгновенные значения параметров состояния близки к средним, и тем, что статистическое равновесие является наиболее вероятным состоянием. На диаграмме состояния равновесное состояние изображается точкой.
Если состояние системы со временем изменяется, то это значит, что в системе происходит процесс. Различают нестатические и квазистатические (равновесные) процессы.
Всякий процесс есть нарушение состояния равновесия. Пусть идеальный газ находится в цилиндре с подвижным поршнем. Если быстро опустить поршень так, что за время D t объем уменьшается на очень малую величину D V, то плотность газа возрастает сначала вблизи поршня. Молекулы слоя газа, прилегающего к поршню, получат за счет совершенной работы над газом дополнительную энергию, и температура слоя повысится. Состояние равновесия газа окажется нарушенным. Через некоторое время молекулы снова равномерно распределятся по всему объему, а полученная молекулами дополнительная энергия распределится между всеми молекулами, и снова установится состояние равновесия.
Процесс перехода системы из неравновесного состояния в равновесное называется релаксацией. Если скорость изменения объема 
гораздо больше скорости восстановления равновесия 
,
,
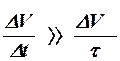то процесс изменения объема будет нестатическим.
Если скорость изменения объема много меньше скорости восстановления равновесия,
,
то изменением состояния системы в любой момент времени можно пренебречь, считая, что система последовательно переходит из одного состояния равновесия в другое, бесконечно близкое к нему. Такой процесс называется квазистатическим.
Подобные рассуждения можно провести относительно изменения других параметров состояния.
На диаграмме состояния квазистатический процесс изображается непрерывной линией. Рассмотрим квазистатические процессы. В основу классификации термодинамических процессов можно положить признак неизменности какого-нибудь из параметров состояния или величин, являющихся функциями параметров состояния. Процессы, когда тот или иной параметр остается неизменным в течение всего процесса, называются ИЗОПРОЦЕССАМИ.
Процесс, происходящий при постоянном давлении p = const, называется ИЗОБАРНЫМ, при постоянном объеме V = const- ИЗОХОРНЫМ, при постоянной температуре Т=const - ИЗОТЕРМИЧЕСКИМ. Если процесс протекает без теплообмена, то его называют АДИАБАТНЫМ. При квазистатическом адиабатном процессе сохраняется энтропия системы S=const, поэтому адиабатный процесс называют иначе ИЗОЭНТРОПИЙНЫМ.
Для идеального газа соответствующие процессы описываются уравнениями:
Гей-Люссака
 ;
| (2) |
Шарля
 ;
| (3) |
Бойля-Мариотта
 ;
| (4) |
Пуассона
 ,
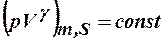| (5) |
где g - коэффициент Пуассона, равный отношению изобарной и изохорной теплоемкостей идеального газа,
 .
| (6) |
Остановимся на адиабатном процессе. Применим к адиабатному процессу первое начало термодинамики:
| δQ = dE + δA. | (7) |
Так как δQ = TdS = 0 при S = const, то
| dE = - δA. | (8) |
Внутренняя энергия Е системы при адиабатном процессе изменяется за счет работы.
Для идеального газа внутренняя энергия зависит только от температуры:
 ,
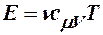| (9) |
поэтому согласно (8) можно записать уравнение
 .
| |
 .
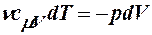| (10) |
При адиабатном расширении dV >0 идеальный газ охлаждается dТ< 0, а при сжатии dV< 0 - нагревается dТ > 0.
Если в (10) подставить 
и учесть соотношение Майера 
, то получим
 .
| (11) |
Проинтегрировав, найдем уравнение Пуассона в параметрах Т, V:
 .
| (12) |
Заменяя в (12) Т~pV по формуле (1), можно получить уравнение Пуассона в параметрах p, V (5).
ОПИСАНИЕ УСТАНОВКИ И ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПУАССОНА
 |
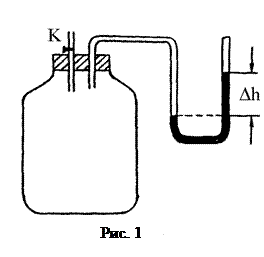Коэффициент Пуассона можно измерить с помощью прибора Клемана-Дезорма (рис. 1), состоящего из стеклянного баллона с воздухом, насоса и водяного манометра. В баллон накачивается с помощью насоса воздух. При этом давление воздуха в баллоне повысится и станет равным
 ,
| (13) |
где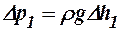 
– превышение давления воздуха в баллоне над атмосферным давлением 
. 
- разность уровней воды в коленах манометра (рис. 1). Открывают на короткое время кран К, чтобы давление в баллоне сравнялось с атмосферным 
, после чего закрывают кран.
Процесс расширения кратковременный, заметного теплообмена между воздухом в баллоне и окружающей средой не происходит, поэтому процесс можно считать адиабатным. После адиабатного расширения температура воздуха в баллоне понизится и станет меньше температуры окружающей среды. В результате теплообмена через некоторый промежуток времени температура воздуха в баллоне сравняется с комнатной. На этом этапе имеет место изохорный процесс нагревания. При этом давление в баллоне возрастает, достигая значения
 ,
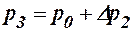| (14) |
где 
- превышение давления в баллоне над атмосферным p0 после изохорного нагрева. Dh2 - разность уровней воды в коленах манометра.
 |
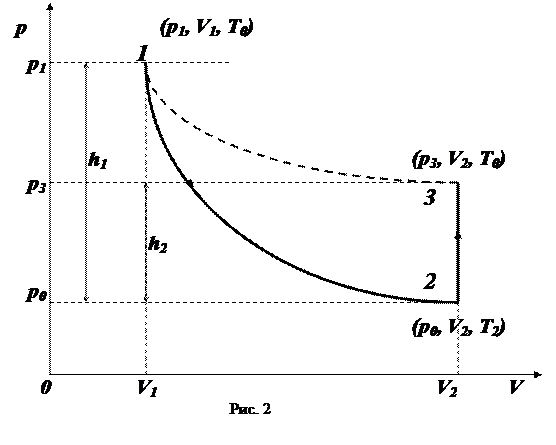Представим на диаграмме состояний в параметрах p, V вышеуказанные процессы (рис. 2). До открытия крана в баллоне находился сжатый воздух объемом V1 при комнатной температуре Т0 и давлении
.Это состояние соответствует т. 1. После того как открыли кран К, воздух адиабатно расширяется до объема V2 и охлаждается до температуры Т2. При этом давление понижается до атмосферного p2 = p0. Это состояние изображается т. 2. Состояния 1 и 2 связаны уравнением Пуассона
 .
| (15) |
После закрытия крана К начинается изохорный процесс нагревания воздуха. По окончании теплообмена в баллоне установится комнатная температура Т0 при давлении p0 > p3. Это состояние изображается т. 3 на диаграмме состояний. Состояния 1 и 3 соответствуют одной и той же температуре Т0, поэтому т. 1 и т. 3 должны принадлежать одной изотерме, а параметры этих состояний связаны уравнением (4):
 .
| (16) |
Из (15) и (16), исключая отношение V2/V1, получим
 .
| (17) |
Учтём (13) и (14):
 .
|
В нашем эксперименте
 ,  ,
|
поэтому можно записать
 .
|
Откуда находим
| (18) |
или, учитывая, что
,  ,
|
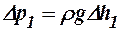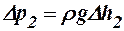получим
 .
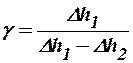| (19) |
Экспериментальное определение коэффициента Пуассона сводится к измерению разности уровней манометра Dh1 и Dh2.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. В баллон с помощью насоса накачивают немного воздуха. При накачивании воздух, сжимаемый поршнем насоса, нагревается. Необходимо выждать некоторое время, чтобы воздух в баллоне снова принял температуру окружающей среды. После этого измеряют разность уровней воды в коленах манометра Dh1 (мм).
2. Открывают кран К. К моменту времени, когда уровни жидкости в коленах манометра сравняются, кран закрывают. Выждав 2-3 минуты, чтобы газ, охлажденный при адиабатном расширении, нагрелся до комнатной температуры, измеряют разность уровней воды в коленах манометра Dh2.
3. По формуле (19) вычисляют значение коэффициента Пуассона gэ.
4. Измерения повторяют 5-7 раз.
5. Находят среднее значение коэффициента Пуассона < gэ >.
6. Выражают коэффициент Пуассона для идеального газа через число степеней свободы. Находят теоретическое значение коэффициента Пуассона gт, считая воздух мономолекулярным двухатомным газом.
7. Вычисляют расхождение между экспериментальным и теоретическим значениями коэффициента Пуассона 
.
ПРОТОКОЛ ИСПЫТАНИЙ
| № | Dh1, мм | Dh2, мм | gэ | < gэ > | gт | e, % |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назовите основные задачи работы. Какие законы применяются для решения этих задач?
2. Выведите расчетную формулу для коэффициента Пуассона методом Клемана-Дезорма.
3. Опишите экспериментальную установку. Из каких основных частей она состоит и для чего предназначен каждый элемент установки?
4. Что такое термодинамическая система? Какие системы называются изолированными? Приведите примеры.
5. Какие термодинамические параметры являются функциями состояния, а какие являются функциями процесса?
6. Какие состояния называются равновесными? Какие процессы называются равновесными?
7. Что такое уравнение состояния? Запишите и проанализируйте уравнение состояния идеального газа.
8. Какие процессы являются изотермическими, изобарическими, изохорическими? Запишите и поясните законы, которым подчиняются приведенные изопроцессы.
9. Что такое релаксация? От чего зависит время релаксации?
10. Выведите уравнение Пуассона.
ЛАБОРАТОРНАЯ РАБОТА № 2.3
