Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Ивановский государственный энергетический университет
имени В.И. Ленина»
Кафедра физики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО МОЛЕКУЛЯРНОЙ ФИЗИКЕ И ТЕРМОДИНАМИКЕ
Иваново 2006
| Составители: | В. Х. КОСТЮК, |
| Г. А. ШМЕЛЁВА | |
| Редактор | В. К. ЛИ–ОРЛОВ |
В методических указаниях приведены основные теоретические сведения и практические рекомендации по выполнению лабораторных работ по молекулярной физике и термодинамике.
Утверждены цикловой методической комиссией ИФФ
Рецензент
кафедра физики ГОУВПО «Ивановский государственный энергетический университет имени В.И.Ленина»
Методические указания к лабораторным работам
по молекулярной физики и термодинамике
Составители: Костюк Владимир Харитонович
Шмелева Галина Александровна
Редактор М.А. Иванова
Лицензия ИД № 05285 от 4июля 2001 г.
Подписано в печать. Формат 60х841/16. Печать плоская.
Усл. печ. л. 1,86. Тираж 150 экз. Заказ
ГОУВПО «Ивановский государственный энергетический
университет им. Ленина»
Отпечатано в РИО ИГЭУ.
153003, г. Иваново, ул. Рабфаковская, 34.
ЛАБОРАТОРНАЯ РАБОТА № 2.1
ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОЙ ВЯЗКОСТИ ВОЗДУХА МЕТОДОМ ПУАЗЕЙЛЯ
ЦЕЛЬ РАБОТЫ
1. Изучение стационарного ламинарного движения несжимаемой жидкости (газа) в изотермических условиях через горизонтальные цилиндрические трубы круглого сечения.
2. Экспериментальное определение динамической вязкости воздуха методом Пуазейля.
3. Количественная оценка средней длины свободного пробега молекул воздуха и их размеров (эффективный диаметр) на основе молекулярно-кинетической теории идеальных газов.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
1. Вискозиметр.
2. Секундомер.
3. Термометр.
4. Барометр.
ВВЕДЕНИЕ
Свойство жидкости (газа) оказывать сопротивление относительному перемещению ее слоев называется ВЯЗКОСТЬЮ. Между слоями жидкости, движущимися с различными скоростями, действуют силы внутреннего трения (силы вязкости).
Слоистое движение вязкой несжимаемой жидкости (газа) называется ламинарным.
Ламинарное движение возникает при движении жидкости в каналах или трубах небольшого сечения с малыми скоростями, а также при движении очень вязких жидкостей.
Рассмотрим, от чего зависят силы вязкого трения. Погрузим в жидкость две параллельные пластинки и будем перемещать верхнюю относительно нижней с постоянной скоростью  (рис. 1). Для этого необходимо приложить постоянную силу
(рис. 1). Для этого необходимо приложить постоянную силу  . Так как пластина не получает ускорения, то действие этой силы уравновешивается другой, равной ей по величине и противоположно направленной силой трения
. Так как пластина не получает ускорения, то действие этой силы уравновешивается другой, равной ей по величине и противоположно направленной силой трения  . Такие силы действуют между любыми слоями жидкости при условии, что они перемещаются друг относительно друга. При этом со стороны более быстрого слоя на более медленный слой действует ускоряющая сила, а со стороны медленного на более быстрый – замедляющая.
. Такие силы действуют между любыми слоями жидкости при условии, что они перемещаются друг относительно друга. При этом со стороны более быстрого слоя на более медленный слой действует ускоряющая сила, а со стороны медленного на более быстрый – замедляющая.
 |
Большинство жидкостей прилипает к поверхности твердых тел, погруженных в жидкость. Мы будем рассматривать только такие жидкости. Слой, прилегающий к верхней пластине, будет двигаться со скоростью
 . Нижняя пластина будет испытывать действие вязкой силы в направлении движения верхней пластины и поэтому она должна прийти в движение. Пусть нижняя пластина неподвижна. Для этого к ней необходимо приложить внешнюю силу, направленную против силы вязкого трения и равную ей. Слой жидкости, прилегающий к нижней пластине, будет неподвижен, а скорость вышележащих слоев будет нарастать, как показано на рис. 1.
. Нижняя пластина будет испытывать действие вязкой силы в направлении движения верхней пластины и поэтому она должна прийти в движение. Пусть нижняя пластина неподвижна. Для этого к ней необходимо приложить внешнюю силу, направленную против силы вязкого трения и равную ей. Слой жидкости, прилегающий к нижней пластине, будет неподвижен, а скорость вышележащих слоев будет нарастать, как показано на рис. 1.
Величина силы вязкого трения зависит от того, как "быстро" меняется скорость слоев с высотой, то есть от величины  , где d – расстояние между пластинами, от площади поверхности S перемещающихся относительно друг друга слоев, а также от природы и состояния жидкости. В нашем случае можно записать
, где d – расстояние между пластинами, от площади поверхности S перемещающихся относительно друг друга слоев, а также от природы и состояния жидкости. В нашем случае можно записать
 , ,
| (1) |
где величина  называется градиентом скорости и характеризует изменение скорости поперек потока жидкости, приходящееся на единицу длины; h – коэффициент внутреннего трения, называемый динамической вязкостью, зависящий от природы жидкости, температуры и давления.
называется градиентом скорости и характеризует изменение скорости поперек потока жидкости, приходящееся на единицу длины; h – коэффициент внутреннего трения, называемый динамической вязкостью, зависящий от природы жидкости, температуры и давления.
Введем понятие поверхностной плотности вязкого трения. Это сила вязкого трения, приходящаяся на единицу поверхности слоев:
 . .
| (2) |
В общем случае распределение (эпюра) скорости V (x) поперек потока может быть нелинейным (рис. 2).

Градиент скорости  зависит от x, и сила вязкого трения для различных слоев будет функцией x. С учётом направления силы вязкого трения можно записать
зависит от x, и сила вязкого трения для различных слоев будет функцией x. С учётом направления силы вязкого трения можно записать
 . .
| (3) |
Соотношение (3) называется законом вязкого трения Ньютона. Из (3) можно установить физический смысл коэффициента h. Динамическая вязкость h численно равна силе вязкости, действующей на единицу площади слоя, при градиенте скорости, равном единице:
 при при 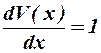 . .
| (4) |
Внутреннее трение является причиной того, что для протекания газа (жидкости) через трубу требуется некоторая разность давлений. Разность давлений тем больше, чем больше коэффициент внутреннего трения h.
 |
Рассмотрим стационарное течение вязкой несжимаемой жидкости (газа) по цилиндрической трубе круглого сечения. Мысленно выделим расположенный вдоль оси трубы цилиндр длиной l и радиусом r (рис. 3). Скорость жидкости в разных точках сечения трубы различна. Она зависит от расстояния до стенок, а градиент скорости есть
 .
.
С внешней стороны на единицу поверхности цилиндра действует сила вязкости
 , ,
|
а на всю поверхность S = 2prl рассматриваемого цилиндра – сила
 .
.
Движение происходит с постоянной скоростью, и сила F должна уравновешивать разность сил давления p1 и p2 на торцах цилиндра.
 ,
,
 .
.
Интегрируя, получаем
 .
.
У стенок трубы при r = R скорость жидкости V = 0. Жидкость прилипает к стенкам трубы. Из этого условия находится постоянная, и окончательно для скорости получаем
 , ,
| (5) |
где Dp = p1 – p2.
Эпюра скорости является параболоидом вращения с меридиальным сечением в виде параболы, которая одинакова для различных сечений трубы. Скорости по сечению трубы растут по квадратичному закону от нуля у стенок до максимального значения на оси трубы:

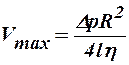 .
.
Вычислим объемный расход жидкости за секунду через все сечение трубы. Разобьём сечение трубы на тонкие кольца радиусом r и шириной dr (рис. 4). Через площадь кольца dS = 2prdr в единицу времени протекает объем жидкости dQ=2prdrV, а через все сечение трубы протекает объем жидкости
 .
.
Интегрируя, получим закон Пуазейля:
 . .
| (6) |
ОПИСАНИЕ УСТАНОВКИ И ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОЙ ВЯЗКОСТИ ВОЗДУХА
В лабораторной работе закон Пуазейля используется для экспериментального определения динамической вязкости воздуха:
 . .
| (7) |
На опыте необходимо измерить перепад давлений Dp и секундный объемный расход воздуха Q (м3/с). Параметры трубы R, l должны быть известны. Вязкость воздуха мала, и для ламинарного движения необходимо обеспечить малую скорость и выбрать трубку небольшого сечения - капиллярную трубку.
 |
Схематично установка для определения вязкости воздуха изображена на рис. 5.
Рис. 5
Из аспиратора А выливается вода, давление в нем понижается, и через капиллярную трубку длиной l = 0,1 м и радиусом R = 10-3 м засасывается воздух, проходящий через осушительный фильтр D с CaCl2. Разность давлений Dp на концах трубки В измеряется водяным манометром С. Для измерения секундного расхода воздуха Q аспиратор А заполняют водой, открывают кран Е и выжидают некоторое время, необходимое для установления стационарного течения. В этом случае разность уровней воды Dh в манометре С будет постоянной. Включают секундомер, одновременно отметив на аспираторе уровень воды. После того как вытечет V = 1 л воды, секундомер выключают. Секундный расход воздуха будет равен объему воды, вытекающему из аспиратора за 1 с:
 . .
| (8) |
Перепад давлений можно выразить через Dh:
| Dp=r gDh, | (9) |
где r =103 кг/м3 – плотность воды, g=9,8 м/с2 – ускорение силы тяжести.
Для динамической вязкости воздуха из (7) с учетом (8) и (9) получаем

| (10) |
или в единицах СИ
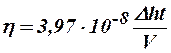 . .
| (11) |
Для расчета вязкости надо выразить Dh в м, t – в с, V – в м3. Результаты измерений и расчета динамической вязкости воздуха заносятся в протокол испытаний. Опыт повторяют 5 раз.
КОЛИЧЕСТВЕННАЯ ОЦЕНКА СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА И ЭФФЕКТИВНОГО СЕЧЕНИЯ СТОЛКНОВЕНИЯ МОЛЕКУЛ
Механизмы переноса в газах (теплопроводность, вязкость, диффузия) с молекулярно-кинетической точки зрения связаны с тепловым движением молекул и их столкновениями между собой, при которых молекулы обмениваются энергией и импульсом. Согласно молекулярно-кинетической теории газов динамическая вязкость газов выражается как
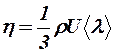 . .
| (12) |
Здесь r – плотность газа (кг/м3); U – тепловая скорость (м/с),
 ; ;
| (13) |
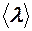 – средняя длина свободного пробега молекул (м),
– средняя длина свободного пробега молекул (м),
 , ,
| (14) |
где s – эффективное сечение столкновения (м2), n – число молекул в единице объема (м-3).
По вязкости газа можно оценить длину свободного пробега 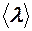 и эффективное сечение s. Получим расчетные формулы для
и эффективное сечение s. Получим расчетные формулы для 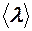 и d. Из (12), учитывая основное уравнение молекулярно-кинетической теории идеальных газов в форме
и d. Из (12), учитывая основное уравнение молекулярно-кинетической теории идеальных газов в форме
 , (15)
, (15)
получим
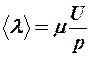
или с учетом (13)
 , ,
| (16) |
где R =8,31×103 Дж/(кмоль×К) – универсальная газовая постоянная, Т –абсолютная температура (K), p – давление газа (Па).
Будем рассматривать воздух как мономолекулярный идеальный газ с молярной массой 29 г/моль. Длина свободного пробега
 . .
| (17) |
Из (14), учитывая равенство
| p = nkТ | (18) |
и соотношение (16), получаем
 , ,
| (19) |
где k = 1,38×10-23 Дж/К - постоянная Больцмана.
Для воздуха
 . .
| (20) |
Измеряя температуру воздуха термометром и атмосферное давление барометром, вычисляем 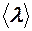 и s по формулам (17) и (20). Диаметр молекул воздуха оцениваем по формуле
и s по формулам (17) и (20). Диаметр молекул воздуха оцениваем по формуле

| (21) |
и сравниваем с табличным значением для молекул N2 и O2: d = 3×10-10м. Результаты измерений и расчетов записать в протокол испытаний.
ПРОТОКОЛ ИСПЫТАНИЙ
| Dh, м | V, м3 | t, c | h, Па×с | p, Па | T, K | 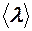 , м , м
| s, м2 | d, м |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назовите основные задачи работы. Какие законы применяются для решения этих задач?
2. Приведите вывод закона Пуазейля, проанализируйте закон.
3. Опишите экспериментальную установку. Из каких основных частей она состоит и для чего предназначен каждый элемент установки?
4. Какой газ называется идеальным? Опишите модель идеального газа.
5. Что такое средняя квадратичная скорость молекул?
6. Запишите и проанализируйте основной закон молекулярно-кинетической теории идеального газа.
7. Какие явления называются явлениями переноса? Какие явления переноса Вы знаете?
8. Что такое вязкость? Запишите и поясните закон Ньютона для вязкого трения.
9. Каков механизм вязкости с точки зрения молекулярно-кинетической теории?
10. Как зависит динамическая вязкость газов от температуры?
11. Дайте определение динамической вязкости и установите её размерность в единицах СИ.
12. Что называется средней длиной свободного пробега молекул идеального газа? Как она связана с динамической вязкостью?
13. Как можно оценить среднюю длину свободного пробега молекул в опыте?
14. Выведите связь средней длины свободного пробега молекул идеального газа и эффективного сечения столкновения молекул. Как связать эффективное сечение столкновения молекул с динамической вязкостью?
15. Сравните диаметр молекул «воздуха» с табличными значениями для молекул азота и кислорода. Проанализируйте результаты.
ЛАБОРАТОРНАЯ РАБОТА № 2.2






