Враща́тельное движе́ние – вид механического движения абсолютно твёрдого тела, при котором его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.
Угловая скорость – изменение углового пути в единицу времени:
,
где 
- угловой путь (угол поворота тела вокруг своей оси). Вектор угловой скорости направлен по оси вращения в соответствие с правилом правого винта (буравчика).
Угловое ускорение 
- изменение угловой скорости тела в единицу времени:
.
Угловое ускорение 
связано с линейным ускорением 
:
, (1)
где - линейное ускорение,
-радиус кривизны траектории движения.
Моментом силы F относительно точки O (рисунок 2) называют вектор, равный векторному произведению радиус-вектора 
, который определяет положение точки приложения силы, на вектор силы 
:
.
Модуль вектора 
равен
(2).
Моментом силы относительно оси Z называют проекцию на эту ось вектора , определенного относительно произвольной точки О данной оси (рисунок 2).
Момент инерции тела -это величина, характеризующая распределение масс в теле и являющаяся мерой инертности тела во вращательном движении. Моментом инерции тела относительно оси Z называется величина, определяемая равенством:
, (3)
где 
– расстояние от оси 
,
массовая плотность,
объем тела.
Для точечного тела массой 
, вращающегося по окружности радиусом 
:
.
Момент инерции – величина аддитивная. Это означает, что момент инерции тела равен сумме моментов инерции его частей.
Момент импульса точечного тела – векторное произведение радиус-вектора 
, определяющего положение точки, на вектор импульса 
:
.
Для вращающегося твердого тела относительно оси вращения:
Динамический закон, который используется для описания движения вращающегося тела, называется основным законом динамики вращательного движения. Он может быть записан следующим образом:
, (4.1)
, (4.2)
, (4.3)
где 
– суммарный (результирующий) момент сил, действующих на тело,
–- момент инерции вращающегося тела.
По существу основной закон динамики вращательного движения – это второй закон Ньютона, записанный через кинематические и динамические характеристики вращательного движения для вращающегося тела.
Проверка соотношений (4) может быть проведена экспериментально с помощью маятника Обербека.
Если в чашку 5 (рисунок 1) положить груз массой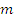 
, то под действием силы натяжения нити 
начнет вращаться с ускорением 
, а груз двигаться вниз с ускорением . Для равноускоренного движения
,
где 
– расстояние, которое проходит груз от начальной(самой верхней) точки движения, до конечной (самой нижней) точки, когда нить полностью размотается со шкива 1 (рисунок 1),
– время движения груза.
Тогда угловое ускорение маятника:
, (5)
где 
– радиус шкива.
Второй закон Ньютона для груза m в проекциях на вертикальную ось:
.
Отсюда 
и момент силы натяжения нити, действующей на маятник:
(6)
В оси маятника действует сила трения, которая создает тормозящий момент 
(остальными силами сопротивления, например аэродинамическими, действующими на все тела маятника, будем пренебрегать). Действие силы трения ведет к уменьшению механической энергии маятника. Поэтому после достижения грузом самой нижней точки, он движется замедленно вверх (т.к. маятник по инерции вращается) и поднимается на высоту 
(в момент остановки маятника). Причем 
< 
. Уменьшение потенциальной энергии груза за все время движения 
равно работе силы трения 
, где -угловой путь, пройденный маятником: 
.
По закону сохранения энергии: 
. Откуда
(7)
Суммируя выражения (6) и (7) найдем результирующий момент сил, действующих на маятник:
(8)
Условия проведения эксперимента на маятнике Обербека в данной лабораторной работе таковы, что в последнем выражении дробь 
(несколько сотых долей %). Поэтому если ей пренебречь, то упрощенно результирующий момент сил может быть найден как
(8´)
Из (4) следует, что если разделить (8) на (5), то можно найти выражение для определения момента инерции вращающегося маятника:
(9)
Таким образом, выражения (5), (8), (9) позволяют найти экспериментально на маятнике Обербека все основные физические величины, входящие в основной закон динамики вращательного движения.
