Момент инерции тела 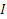 – это физическая величина, являющаяся мерой инертности тела во вращательном движении. Для точечного тела массой
– это физическая величина, являющаяся мерой инертности тела во вращательном движении. Для точечного тела массой 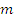 , вращающегося по окружности радиусом
, вращающегося по окружности радиусом  , момент инерции определяется формулой:
, момент инерции определяется формулой:
 . (1)
. (1)
В соответствие с этим для тела с бесконечно малой массой  :
:
 (2)
(2)
Момент инерции любого тела можно рассчитать, используя выражение (2). Для этого тело «разбивают» на микрообъемы с массами  . Считая каждый из таких микрообъемов точечным телом, находят момент инерции
. Считая каждый из таких микрообъемов точечным телом, находят момент инерции  каждого из них по формуле (2) и все
каждого из них по формуле (2) и все  суммируют:
суммируют:
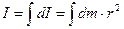 (3)
(3)
Моменты инерции некоторых тел правильной геометрической формы относительно оси, проходящей через центр тяжести, определятся:
а) для стержня
 . (4)
. (4)
б) для диска
 . (5)
. (5)
в) для кольца
 , (6)
, (6)
где  - масса диска;
- масса диска;
 - радиус диска;
- радиус диска;
 - масса кольца;
- масса кольца;
 - внутренний радиус кольца;
- внутренний радиус кольца;
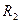 - внешний радиус кольца;
- внешний радиус кольца;
 - масса стержня;
- масса стержня;
 – длина стержня.
– длина стержня.
Момент инерции 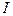 тела относительно произвольной оси определяется суммой момента инерции
тела относительно произвольной оси определяется суммой момента инерции  тела относительно параллельной ей оси, проходящей через центр масс тела и произведения массы тела на квадрат расстояния
тела относительно параллельной ей оси, проходящей через центр масс тела и произведения массы тела на квадрат расстояния  между этими осями, согласно теореме Штейнера:
между этими осями, согласно теореме Штейнера:
 . (7)
. (7)
Экспериментально момент инерции тела можно определить с помощью крутильного маятника (рисунке 1). Если верхнюю платформу повернуть на малый угол, то нижняя платформа будет совершать крутильные колебания вокруг оси ОО΄.
Пренебрегая силами трения в системе, можно считать постоянной полную механическую энергию. В точке максимального закручивания платформа поднимается на высоту 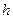 , при этом полная энергия равна потенциальной энергии
, при этом полная энергия равна потенциальной энергии
 ,
,
где  -масса платформы.
-масса платформы.
При прохождении положения равновесия платформа движется с максимальной угловой скоростью  , при этом полная энергия равна кинетической
, при этом полная энергия равна кинетической
 ,
,
где 
 – момент инерции платформы..
– момент инерции платформы..
По закону сохранения энергии:  .
.
Из этого уравнения получим:
 (8)
(8)
Так как малые колебания можно считать гармоническими, то колебания нижней платформы проходят по закону:
 ,
,
где  – максимальный угол поворота;
– максимальный угол поворота;
 - период колебаний.
- период колебаний.
Угловая скорость: 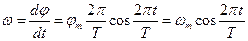 .
.
То есть
 . (9)
. (9)
Из геометрических соображений [1]:
 . (10)
. (10)
Тогда из (8), (9) и (10):
 , (11)
, (11)
где 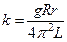 . (12)
. (12)
Используя формулу (11) можно рассчитать момент инерции, как ненагруженной платформы  , так и нагруженной платформы
, так и нагруженной платформы  .Пользуясь свойством аддитивности момента инерции, момент инерции тела на платформе
.Пользуясь свойством аддитивности момента инерции, момент инерции тела на платформе  рассчитывается как:
рассчитывается как:
 . (13)
. (13)
Порядок выполнения работы и обработка экспериментальных данных
Задание 1. Определение момента инерции тел
1. Занести данные установки ( ,
,  ,
,  ,
,  ) в таблицу 1 и по заданию преподавателя параметры тел (для диска – массу
) в таблицу 1 и по заданию преподавателя параметры тел (для диска – массу  и радиус
и радиус  , для кольца - массу кольца
, для кольца - массу кольца  , его внутренний
, его внутренний  и внешний
и внешний 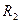 радиусы, для стержня – массу
радиусы, для стержня – массу  и длину
и длину  ) в таблицу 2.
) в таблицу 2.
2. Поворотом верхней платформы вывести нижнюю ненагруженную платформу из положения равновесия так, чтобы она совершала крутильные колебания с амплитудой 5-10°. Измерить время t полных 50  100 колебаний и внести в таблицу 1.
100 колебаний и внести в таблицу 1.
3. Повторить пункт 2 для платформы с телом (стержень, кольцо или диск), помещенным в центр платформы.
4. Вычислить периоды колебаний  (ненагруженной платформы), и
(ненагруженной платформы), и 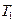 (ненагруженной платформы) по формуле
(ненагруженной платформы) по формуле  ,
,
где n – число колебаний.
5. Рассчитать  по формуле (12).
по формуле (12).
6. Рассчитать момент инерции ненагруженной платформы

7. Рассчитать относительную погрешность измерения момента инерции ненагруженной платформы  и записать в таблицу 1.
и записать в таблицу 1.
Так как измерение проводиться однократно, то погрешность  определяется исходя из погрешности измерительного прибора. то есть в данном случае секундомера.
определяется исходя из погрешности измерительного прибора. то есть в данном случае секундомера.
8. Вычислить абсолютную погрешность измерения момента инерции ненагруженной платформы  и записать в таблицу 1.
и записать в таблицу 1.
9. Рассчитать момент инерции нагруженной платформы по формуле:

где  - масса платформы,
- масса платформы,  – масса тела.
– масса тела.
10. Рассчитать относительную погрешность измерения момента инерции нагруженной платформы  .
.
11. Вычислить абсолютную погрешность измерения момента инерции нагруженной платформы:  .
.
12. Пользуясь свойством аддитивности, рассчитать момент инерции тела  .
.
13. Рассчитать абсолютную погрешность измерения момента инерции тела  и записать в таблицу 2.
и записать в таблицу 2.
14. Используя формулы (4), (5), (6) рассчитать теоретическое значение момента инерции тела  .
.
15. Рассчитать относительную погрешность определения момента инерции тела по отношению к теоретической по формуле:

16. Результаты занести в таблицу 2.
17. Проанализировать результаты и сделать выводы.
Таблица 1
| Параметры установки | n | t,с |  ,с ,с
|  , кг∙м2 , кг∙м2
| 
| 
|
 , м , м
 , м , м
 , м , м
 , кг , кг
|
Таблица 2
| Параметры тел | n | t, с | T1,с |  , кг∙м2 , кг∙м2
|  , кг∙м2 , кг∙м2
| 
|  ,% ,%
|
стержень
 , м , м
 , кг , кг
| |||||||
диск
 , м , м
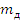 , кг , кг
| |||||||
кольцо
 , м , м
 , м , м
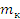 , кг , кг
|
Задание 1а. Определение момента инерции тел
1. Занести данные установки ( ,
,  ,
,  ,
,  ) в таблицу 1а и по заданию преподавателя параметры тела, с которым будет проводится эксперимент (для диска – массу
) в таблицу 1а и по заданию преподавателя параметры тела, с которым будет проводится эксперимент (для диска – массу  и радиус
и радиус  , для кольца - массу кольца
, для кольца - массу кольца  , его внутренний
, его внутренний  и внешний
и внешний 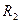 радиусы, для стержня – массу
радиусы, для стержня – массу  и длину
и длину  ), в таблицу 2а.
), в таблицу 2а.
2. Поворотом верхней платформы вывести нижнюю ненагруженную платформу из положения равновесия так, чтобы она совершала крутильные колебания с амплитудой 5-10°.
Измерить время  полных
полных  =10 колебаний ненагруженного маятника
=10 колебаний ненагруженного маятника  =8-10 раз и внести в таблицу 1a.
=8-10 раз и внести в таблицу 1a.
3. Повторить пункт 2 для платформы с телом (стержень, кольцо или диск), помещенным в центр платформы. Полученные данные занести в таблицу 2а.
4. Для каждого измерения рассчитайте период колебаний  =
= 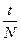 и средние значения периода колебаний ненагруженного
и средние значения периода колебаний ненагруженного 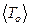 и нагруженного маятника
и нагруженного маятника  . Данные расчетов занесите в таблицы 1а и 2а.
. Данные расчетов занесите в таблицы 1а и 2а.
5. По формуле 6 (стр.7) рассчитайте средние квадратические погрешности  и
и 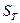 определения
определения  и
и  . Полученные данные занесите в таблицы 1а и 2а.
. Полученные данные занесите в таблицы 1а и 2а.
6. Рассчитать  по формуле (12).
по формуле (12).
7. Рассчитать и занести в таблицу 1а среднее значение момента инерции ненагруженной платформы:

8. Рассчитать и занести в таблицу 2а среднее значение момента инерции нагруженной платформы:

где  - масса платформы,
- масса платформы,  – масса тела.
– масса тела.
9. Пользуясь свойством аддитивности, рассчитать момент инерции тела  и занести его в таблицу 2а.
и занести его в таблицу 2а.
10. По формуле  найдите среднюю квадратическую ошибку определения
найдите среднюю квадратическую ошибку определения 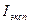 .
.
11. Используя формулу (8) на стр.8 рассчитайте доверительный интервал  определения
определения  .
.
12. Окончательный результат экспериментального определения момента инерции тел запишите в виде: 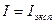
 .
.
13. Рассчитайте теоретическое значение момента инерции исследуемого тела по одной из формул (4), (5), (6) и сравните его с экспериментальным.
14. Проанализируйте полученные результаты и сделайте выводы.
Таблица 1а
Ненагруженный маятник
| Параметры установки | n | t, с |  , с , с
|  , с , с
| 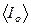 , кг∙м2 , кг∙м2
| 
|
 , м , м
 , м , м
 , м , м
 , кг , кг
| ||||||
| ... | ||||||
Таблица 2а
Нагруженный маятник
| Параметры тел | n | t,с |  ,с ,с
|  , с , с
|  , кг∙м2 , кг∙м2
|  , кг∙м2 , кг∙м2
| 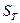
|
стержень
 , м , м
 , кг , кг
| |||||||
диск
 , м , м
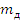 , кг , кг
| . . | ||||||
кольцо
 , м , м
 , м , м
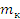 , кг , кг
|
Задание 2. Проверка свойства аддитивности момента инерции
1. Записать в таблицу 3 массу платформы 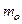 , массу кольца
, массу кольца 
 и параметры установки.
и параметры установки.
2. Установить одно кольцо в центре платформы и измерить время 50  100 полных колебаний. Занести результат в таблицу 3.
100 полных колебаний. Занести результат в таблицу 3.
3. Вычислить период колебания по формуле  ,
,
где n – число колебаний.
4. Пункты 1-3 повторить для двух и трех колец, одновременно установленных в центре платформы.
5. Рассчитать  по формуле (12)
по формуле (12)
6. Рассчитать моменты инерции нагруженной платформы по формуле
 ,
,
где 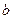 - количество колец (
- количество колец ( 1, 2, 3), установленных на платформе. Полученные данные занести в таблицу 3.
1, 2, 3), установленных на платформе. Полученные данные занести в таблицу 3.
7. Построить график зависимости  (рисунке 2). Продолжив график до пересечения с осью
(рисунке 2). Продолжив график до пересечения с осью  , найти момент инерции ненагруженной платформы
, найти момент инерции ненагруженной платформы  . Определить по графику
. Определить по графику  ,
, 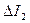 ,
,  .
.
8. Все результаты занести в таблицу 3.
9. Проанализировать результаты расчетов и сделать выводы.

Рис.2.
Таблица 3
| Параметры кольца и установки | кол-во ко-лец | n | t, с |  ,с ,с
|  , кг∙м2 , кг∙м2
|  , кг∙м2 , кг∙м2
| 
| 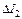
| 
|
L, м
R, м
r, м
mo, кг
Dк , м
dк, м
 , кг , кг
| |||||||||
Задание 3. Исследование зависимости момента инерции тела от расстояния между его центром инерции и осью вращения (проверка теоремы Штейнера)
1. Определить момент инерции ненагруженной платформы, выполнив пункты 1, 2, 4, 5, 6, 7, 8 задания 1.
2. Измерить параметры тел, с которыми будет производиться эксперимент (по указанию преподавателя). Для дисков – массу  и радиус
и радиус  , для стержней – массу
, для стержней – массу  и длину
и длину  . Занести данные в таблицу 4.
. Занести данные в таблицу 4.
3. Поместить тела симметрично относительно центра платформы на минимальное расстоянии  . Занести значения
. Занести значения  в таблицу 4.
в таблицу 4.
4. Измерить время 10  50 полных колебаний и занести в таблицу 4.
50 полных колебаний и занести в таблицу 4.
5. Последовательно увеличивая расстояние  , для каждого из них выполнить пункт 4. Занести данные в таблицу 4.
, для каждого из них выполнить пункт 4. Занести данные в таблицу 4.
6. Для каждого  вычислить периоды колебаний по формуле
вычислить периоды колебаний по формуле
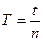 .
.
7. Рассчитать моменты инерции нагруженной платформы по формуле для каждого случая
 ,
,
где 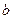 - количество тел, расположенных на платформе;
- количество тел, расположенных на платформе;
 - масса платформы;
- масса платформы;
 – масса тела.
– масса тела.
8. Пользуясь свойством аддитивности, рассчитать для каждого  момент инерции тел:
момент инерции тел: 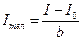 . Занести данные в табл. 4.
. Занести данные в табл. 4.
9. Построить графики зависимости  (a),
(a),  (a 2).
(a 2).
10. Проанализировать полученные данные и сделать выводы по работе.
Таблица 4
| Параметры тел | а, м | n | t, с | T, с |  , кг∙м2 , кг∙м2
|  , кг∙м2 , кг∙м2
|
стержень
 , м , м
 , кг
диск , кг
диск
 , м , м
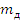 , кг , кг
| ||||||
| . . . |
Вопросы для контроля
1.Что такое момент инерции тела? В чем состоит смысл этой физической характеристики?
2.Как вычисляется момент инерции тела относительно точки и относительно оси?
3.Сформулируйте теорему Штейнера. В каком случае ее применяют?
4. Каков характер зависимости момента инерции от расстояния, на котором находится тело от оси вращения?
5.Как экспериментально определяется момент инерции тела в данной лабораторной работе?
6.Какие законы сохранения применяются для вывода расчетных формул?
Библиографический список
1.Сивухин Д.В. Общий курс физики. Т.1.. «М.: ФИЗМАТЛИТ МФТИ», 2002. 560 с. §42.
2.Савельев И.В. Курс общей физики. Т.1. М. «Наука», 1989. 416 с. §31, 32.
3.Трофимова Т.И. Курс физики. М. «Высшая школа», 1997. 542 с.§16.






