Физические основы гемодинамики

Гидродинамика — это раздел физики, изу­чающий законы движения и силы взаимодей­ствия в жидкостях.

Механические свойства жидкости обусловлены силами, дей­ствующими между молекулами. Рассмотрим стационарное тече­ние идеальной жидкости по трубе переменного сечения.

Течение жидкости называется стационар­ным или устано­вившимся, если с течением времени скорость частиц жидко­сти в каж­дой точке потока не изменяется.

Идеальной называется жидкость, не обла­дающая внутрен­ним трением и несжимае­мая. К такой жидкости по своим свойствам близок гелий при сверхнизких температурах. Для идеальной жидкости при стационарном течении скоро­сти течения обратно пропор­циональны площадям поперечного сечения.

υ₁/υ₂=S₁/S₂ υS=const

Это уравнение неразрывнос­ти струи. Уравнение Бернулли и его следствие.

Для идеальной жидкости, при установив­шемся течении сумма трех энергий (потенци­альной энергии сил давления, потенциальной энергии сил тя­жести и кинетической энер­гии) для любого сечения есть величи­на посто­янная.

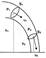
P₁V + mgh₁ + (mυ₁²)/2 = P₂V = mgh₂ + (mυ₂²)/2

PV + mgh + (mυ²)/2 =const

Уравнение Бернулли может быть выражено и в другом виде. Поделим все члены уравнения на V.

(PV)/V + (mgh)/V + (mυ²)/2V = const

P + pgh + (pυ²)/2 = const

При стационарном течении идеальной жидкости сумма трех давлений есть величина постоянная в любом поперечном сечении потока.

Р - называется статическим давлением; pgh - гидростати­ческим давлением; pυ² /2 - динамиче­ским давлением. Рас­смотрим физическую сущность этих видов давлений в жидкости.

Статическое или истинное давление - это давление, с кото­рым один слой жидкости давит на другой. Статическое давление может созда­ваться различными внешними причинами (за счёт ра­боты насоса, за счёт потенциальной энергии воды в водонапор­ной башне и т.д.).

Гидростатическое давление обусловлено весовым давлением вышележащего слоя (столба) жидкости на нижележащий.

Динамическое давление - это давление, созда­ваемое движу­щейся жидкостью. Оно проявля­ется при торможении жидкости и обусловлено кинетической энер­гией частиц жидкости.

Измеряется статическое дав­ление при помощи прямой ма­нометрической трубки, плос­кость отверстия которой распо­ложена параллельно движению жидкости. Полное давление из­меряется манометрической

трубкой, изогнутой под прямым углом навстречу движению жид­кости. Это давление является суммой статического и динамического давлений.

 

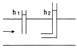
Динамическое давление определяют по разности между пол­ным и измеренным одновременно статическим давлением. Рдин= Рn - Рст В нашем примере Рдин= h₂ - h₁

Единицы измерения давления: СИ - Н/м² [Па], СГС - дн/см², 1Па = 10 дн/см².

Внесистемные единицы давления: техническая атмосфера (ат), 1ат = к Гс/см² = 9,8 10⁴Па,

физическая атмосфера (атм), 1атм = 760 мм.рт.ст. = 1,013 10⁵ Па, 1мм.рт.ст. = 13.6 мм.вод.ст.

В метеорологии применяется единица давления, называемая баром, 1 бар = 10⁵ Па = 750 мм.рт.ст.

Рассмотрим течение идеальной жидкости по горизонтальной трубе переменного сечения. Опыт показывает, что статическое давление в узкой части меньше, чем в широкой. Это явление свя­зано с тем, что в узкой части трубы скорость выше, чем в широ­кой. Так как трубка располо­жена горизонтально, то уравнение Бернулли выглядит следующим образом:

P₁ + (pυ₁²)/2 = P₂ +(pυ₂²)/2

Так как сечение S, > S₂, то на основании уравне­ния неразрыв­ности струи υ2 > υ1. Чтобы сохра­нить равенство в уравнении Бернулли необхо­димо Р, > Р₂. Если Р₂ будет меньше атмосферного давления, тогда в систему будет засасываться воздух - это явле­ние получило название гидроди­намического парадокса. На осно­ве этого явления в медицинской практике используется водо­струйный насос и ингалятор. Они просты по устрой­ству, бесшумны в работе, не требуют смазки, гигиеничны.

 

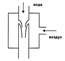
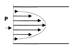
Пусть по горизонтальной трубе одинакового сечения движет­ся реальная вязкая жидкость (Ньютоновская) под давлением Р. Так как давление на все слои одинаково, то можно ожидать одинаковую скорость движения всех слоев. Однако опыт показывает, что скорость слоев увеличивается к центру трубы. Если жидкость смачивает стенки трубы, то скорость первого слоя ровна нулю вследствие сильного взаимодействия молекул стенок трубки и молекул жидкости. В последующих слоях она увеличива­ется постепенно от слоя к слою, вследствие взаимодействия моле­кул жидкости друг с другом. Эти силы взаимодействия между слоями жидкости носят название сил внутрен­него трения или сил вязкости. Они обусловлены:

1. Потенциальными силами взаимо­действия между молекулами жидкости.

2. Перемещением молекул жидкости из одного слоя в другой.

Например: молекулы 3-го слоя, обладающие меньшей кинети­ческой энергией по сравнению с молекулами 4-го слоя, переме­щаясь в него, уменьшают общую кинетическую энергию, т.е. как бы затормаживают его.Было выяснено опытным путём, что силы внутреннего трения между слоями жидкости зависят:

1. От площади соприкасающихся слоев Fη ~ S

2. От градиента скорости Fη ~ dυ/dx

Физический смысл градиента скорости:

Градиентом любой физической величины называется изме­нение этой величины, отнесён­ное к расстоянию, вдоль которого это изменение происходит.

3. Силы внутреннего трения зависят от при­роды жидкости, так как молекулы различных жидкостей находятся на различных расстояниях и имеют различную скорость, а следовательно и ки­нетическую энергию. Эта зависимость учиты­вается коэффициен­том вязкости - η. Таким образом, силы внутреннего трения зави­сят от природы жидкости, прямо пропорциональны градиенту скорости и площади соприкасаю­щихся слоев.

Fη = η (dυ/dx)S

Эта формула получила название формулы Ньютона. Если пло­щадь соприкасающихся слоев S = 1 и градиент скорости dυ/dx = 1, то Fтр = η

Коэффициентом вязкости или вязкостью жидкости назы­вается величина численно равная силе трения, возникающей между двумя слоями жидкости, соприкасающимися на площа­ди равной единице и при градиенте скорости между ними рав­ным единице.

Коэффициент вязкости измеряется в системе СИ: η =Fηdx/Sdυ; Н м / м² (м/с) = Н с / м² = Па с

В системе СГС: Пуаз (Пз) = дн с / см²; Н с / м² = 10⁵ дн с / 10⁴ см² = 10 Пз. В медицине принято измерять вязкость в Пуазах. Коэффициент вязкости зависит не только от природы жидко­сти, но и от температуры. С повышением темпе­ратуры коэффи­циент вязкости уменьшается. Это объясняется тем, что с повыше­нием температуры расстояния между молекулами увеличивают­ся, а силы взаимодействия ослабляются.

Ввиду больших трудностей, возникающих при непосредствен­ном измерении вязкости её определяют косвенным путём. Наи­большее применение имеют методы: падающего шарика и капил­лярного визкозиметра. Метод падающего шарика основан на законе Стокса. Стокс устано­вил, что на небольшое тело шаровидной формы, перемещающееся в жидкости, действует сила трения, прямо про­порциональная радиусу этого тела, его скорости и коэффициенту вязкости жидкости.

Fтр = 6πηrυ

Если бросить в жидкость металлический шарик диаметром 0,2—0,3 мм, то он будет двигаться в жидкости равномерно. На движу­щийся шарик будут действовать три силы

1. Сила тяжести Р = mg, направленная верти­кально вниз.

2. Выталкивающая сила FB, направленная вертикально вверх.

3. Сила трения FTp, направленная также верти­кально вверх.

По первому закону Ньютона тело двига­ется равномерно, если равнодействующая всех сил, действующих на него, равна 0.

Р = Fтр + Fв, откуда Fтр = Р - Fв

По закону Стокса Fтр = 6πηrυ,

P = mg; m = p_TV; P=p_TV_Tg =4/3 πr³p_Tg

По закону Архимеда Fвыт = p_жV_Tg = 4/3 πr³р_жg

6πηrυ=4/3 πr³g (p_Т – p_Ж) η=2/9 (gr²(p_Т - p_Ж)/υ)

Радиус шарика можно измерить с помощью микроскопа с окулярным микрометром, скорость движения шарика можно определить по формуле V = s /t, измерив линейкой s, а секундо­мером - t. Плотность вещества шарика и исследуемой жидко­сти найдём из специальных таблиц при заданной температуре. По приведенной формуле можно вычислить коэффициент вяз­кости. Метод требует большого количества жидкости, жид­кость должна быть прозрачной. Метод довольно точен, используется в санитарии. В медицинской практике для определения коэффициента вяз­кости крови, спиномозговой жидкости и других биологических жидкостей пользуются методом капиллярного вискозиметра, ос­нованный на законе Гагена-Пуазейля. Они установили, что объём жидкости, протекающей через попереч­ное сечение капилляра (R<1мм) в единицу времени прямо пропорционален R⁴, dP/dl и обратно пропорционален η, коэффициент пропорци­ональности в системе СИ равен π/8.

Q=(πR⁴dP)/(8ηdl)

где dP/dl — градиент давления, dP — разность давлений в начале и в конце капилляра, dl — длина капилляра. При пропускании жидкостей через капилляры с одинаковым радиусом при одинаковом градиенте давления, получим:

V₁/t = πR⁴/8η₁dl объём 1 жидкости

V₂/t = πR⁴/8η₂dl объем 2 жидкости

Найдём относительную вязкость, поделив 1 выражение на 2.

η₂/η₁ = V₁/V₂ - формула Гагена-Пуазейля.

Вискозиметр состоит из двух пипеток - капилля­ров, укреплённых на общей подставке. Один капилляр имеет кран. Сначала втягивая воздух заполняют капилляр (б) стандарт­ной жидкостью, как правило водой, до нулевого деления, закры­ва­ют кран и затем заполняют капилляр (а) исследуемой жидкостью до нулевого деления. Открыв кран, втягивают обе жидкости одно­временно так, чтобы исследуемая жидкость дошла до деления.

 

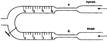
Тогда число делений трубки (б) укажет относи­тельную вякость. Зная η₁, определим η₂ по формуле:

η₂ = η₁V₁

Преимущество и недостатки этого метода:

1. Позволяет измерять вязкость небольшого количества.жид­кости;

2. Быстрота измерения (особенно для крови — быстро свёр­тывается);

3. Измерение вязкости непрозрачных жидкостей.

Недостаток — малая точность ввиду отсутствия стандарта. Течение жидкости называется лами­нарным или слоистым, если поток жидкости представляет собой совокупность слоев, пе­ремещающихся относительно друг друга без перемешивания. При некоторой высокой скоро­сти течение становится турбулентным (вихре­вым), когда происходит перемешивание слоев жидкости. При турбулентном течении жидкости возрастают силы трения, а следовательно и работа по преодолению сил трения. Это тече­ние жидкости сопровождается звуковым феноменом.

Скорость, при которой ламинарное течение переходит в турбулентное называется критической (υ кр.)

Величина этой скорости зависит от вязкости жидкости, радиуса трубки, плотности жидкости и состояния внутренней поверхности. Критическая скорость вычисляется по формуле:

υкр = (R_сеη)/pD

где η - вязкость жидкости, р - плотность, D - диаметр трубки. Безразмерная величина R_се называется числом Рейнольдса. Для гладких трубок R_се = 2300, для трубок с шероховатыми поверхнос­тями эта величина меньше. Течение крови в артериях при нормальных условиях является ламинарным. Турбулентность проявля­ется только в некоторых ме­стах, например, за полулунными клапанами аорты. В некоторых, патологических случаях, при сужении кровенос­ных сосудов, по­роках сердца, изменении коэф­фициента вязкости крови, турбулен­тность распространяется на более длинные участки артерии, что может служить диагностическим целям. При течении идеальной жидкости по горизонтальной трубе постоянного сечения гидростатическое давление в любом сече­нии одинаково (pgh₁ = pgh₂ =...), h₁ = h₂ =..., динами­ческое давле­ние так же одинаково в любом сечении (pυ₁²/ 2 = рυ₂² / 2 =...), т.к. υ₁ = υ₂=... по уравнению неразрывности струи. Следовательно и статическое давление постоянно по всей длине трубы на основа­нии уравнения Бернулли (Р₁ = Р₂). Для реальной жидкости гидростатическое и динамическое дав­ления в любом сечении одинаковы по той же причине, что и для идеаль­ной жидкости. Однако уравнение Бернулли для реальной жидкости, как частный случай закона сохранения энергии, должно включать работу против сил трения.

P₁V = P₂V + A_TP или P₁V = P₂V + F_TPL

Следовательно, т. к. расстояние от начала трубы L увеличива­ется, то Р₂ уменьшается. Это под­тверждается и экспериментально. Манометриче­ские трубки, вставленные в стенку тру­бы, измеряют статическое давление и оно посте­пенно уменьшает­ся.

Величина градиента давления зависит:

1. От коэффициента вязкости жидкости, т.к. Fтр ~ η,

2.От скорости течения жидкости прямо пропор­ционально, т.к. сила сопротивления возрастает пропорционально скорости,

3. Если труба разветвляется, то от числа разветв­лений - пря­мо пропорционально.

Движение жидкости по трубам с эластичными стенками отли­чается от движения жидкости по трубам с упругими стенками своей непрерывно­стью. Можно провести аналогию между законом Пуазейля и Ома для участка цепи

Q=(πr⁴dP)/(8ηL), J=U/R

Разность потенциалов U соответствует разности давлений на концах трубы dP, сила тока J соот­ветствует количеству жидкости Q, а электриче­ское сопротивление R - гидравлическому сопро­тивлению X

Q=(dP)/X, X=(8ηL)/ (πr⁴)

Гидравлическое сопротивление X пропорцио­нально вязкости η, длине трубы L и обратно пропорционально радиусу трубы в четвертой степени. Общее гидравлическое сопротивление после­довательных и параллельных участков сосудов подсчитываются также как и электриче­ское сопротивление;

Хо6щ = X1 + Х2 + Х3 + ... - при последователь­ном соединении,

1 / Хо6щ= 1 / X1 + 1 / Х2 + 1 / Х3 +... — при параллельном со­единении

Рассмотрим особенности течения крови по эластичным сосу­дам. Источником энергии, под действием которого осуществляет­ся перемеще­ние крови, является сердце. При сокращении левого желудочка в аорту, заполненную кровью, выбрасывается допол­нительно несколько десятков мл. крови, так называемый ударный объём. Давление в аорте повышается - это давление называется систолическим. При этом эластичные стенки аорты дают прирост объема AV, а часть полной энергии переходит в потен­циальную энергию деформации сосудистой стенки, но так как обратного тока крови нет (полулунный клапан закрыт), то сокращение стенки облегчает перемещение крови по сосуду и способствует её продвижению дальше. Эластич­ность сосудистых стенок создает непрерывное те­чение крови в кровеносных сосудах. Импульс давления распространяется по сосудистым стенкам и называется пульсовой волной. Ско­рость его распространения зна­чительно выше средней скорости течения крови.

υ _исп .=((Eh)/2pr))^1/2

где Е - модуль упругости сосудистой стенки, h - толщина стен­ки, г - радиус сосуда, р - плотность. С возрастом, когда начинает усиленно отклады­ваться холесте­рин в стенках сосудов (атероскле­роз), модуль упругости сосудис­той стенки увеличивается, увеличивается и скорость пульсо­вой волны, это может произойти и при других патологических про­цессах, поэтому определение скорости пульсовой волны имеет диагностиче­ское значение при различных заболеваниях. Метод графической регистрации пульсовой волны называется сфигмографией. Тензодатчики регистрируют пульс в двух точках, разно удален­ных от сердца (сонная и лучевая артерии) и по изве­стному расстоянию между сердцем и точками начала регистра­ции импульса опреде­ляют отношение пути, проходимое пульсо­вой волной за время t, т.е. скорость.

Моделирование. Механическая и электриче­ская модели кровообращения

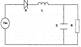
В качестве механической модели можно рас­сматри­вать замкнутую систему из множества разветвленных горизон­тальных трубок с эла­стичными стенками, движение жидкости в кото­рых происходит под действием ритмически ра­ботающего поршня насоса. Под действием поршня жидкость поступает в аорту и круп­ные артерии. Дальше она поступает в прекапилляр­ные сосуды (мелкие артерии и артериолы), об­менные сосуды капилляры, венулы и вены. Ниже на этом рисунке представлен график изменения давле­ния крови в артериальной системе кровооб­ращения. В поршне­вом насосе (левом желу­дочке) давление меняется от О до макси­мального значения и обратно. В аорте и артериях давление пуль­сирует от систолического (в момент выбра­сывания ударного объема крови в аорту) до диа­столического когда левый желу­дочек находится в состоянии покоя. Среднее давление в этих со­судах уменьшается незначи­тельно. Подобные пульсации давления на­блюдаются в мелких ар­териях и артериолах, постепенно затухая. При этом среднее значение давления в артериолах изменяется значительно (градиент давления наи­больший). В капиллярах пуль­сации давления от­сутствуют. Градиент давления также значите­лен,но меньше чем в артериолах. Причина значи­тельного падения давления в артериолах и ка­пиллярах в большом числе разветвле­ний. Даль­нейшее понижение давления наблюдается в ве­нулах и венах. Элек­трической моделью сердца может быть пред­ставленная на рисунке электри­ческая схема. Генератор электрического напря­жения (ГЕН) служит аналогом мышечного ис­точника энер­гии сердца. Диод (Д) — выпрями­тель — аналог аортального кла­пана. Конденсатор (С) накапли­вает заряд, а затем разряжается на со­противление R(x). Роль конденсатора играет аорта, a R(x) пери­ферическая сосудистая система, ее гидрав­лическое сопротивле­ние X, L характе­ризует инерционные свойства электрической цепи, что является аналогом массы ударного объ­ема крови.