Аберрации, свойственные линзам, у глаз почти не ощущаются. Сферическая аберрация незаметна ввиду малости зрачка и проявляется лишь в сумерках, когда зрачок расширен: изображения не резки. Хотя глаз и не является ахроматической системой, однако хроматическая аберрация не ощущается из-за избирательной видимости излучения и малого размера зрачка. Астигматизм косых пучков не имеет места, т.к. глаз всегда устанавливается в направлении наблюдаемого предмета. Исключение составляет лишь астигматизм, обусловленный ассиметрией оптической системы (несферическая форма роговицы или хрусталика). Это проявляется, в частности, в неспособности глаза одинаково резко видеть взаимно перпендикулярные линии на испытательной таблице. Такой недостаток глаза компенсируют специальными очками с цилиндрическими линзами. Оптической системе глаза свойственны некоторые специфические недостатки. В нормальном глазу, при отсутствии аккомодации, изображение предмета совпадает с сетчаткой - такой глаз называют эмметропическим, а если это условие не выполняется - аметропическим. Наиболее распространенными видами аметропии является близорукость (миопия) и дальнозоркость (гиперметропия).
Близорукость - недостаток глаза, состоящий в том, что, при отсутствии аккомодации, изображение предмета лежит впереди сетчатки; в случае дальнозоркости изображение предмета, при отсутствии аккомодации, лежит за сетчаткой. Для коррекции близорукости глаза применяют рассеивающую линзу, дальнозоркости - собирающую.
Фотометрия. Фотоэффект
Основной фотометрической величиной является световой поток - это среднее количество световой энергии, проходящей за единицу времени через заданную поверхность.
Ф = dW/dt
Здесь dW — количество энергии, проходящей через заданную поверхность за время dt. Понятие силы света вводится с помощью представления о точечном источнике света. Источник света считается точечным, если его размеры малы в сравнении с расстоянием до места наблюдения и если он испускает свет равномерно по всем направлениям.
Сила света измеряется световым потоком, создаваемым точечным источником света в единичном телесном угле ω.
J = Ф/ω
Телесным углом называется часть пространства, ограниченная конической поверхностью и измеряемая отношением площади S, вырезаемой этим углом на поверхности сферы, к квадрату радиуса сферы R:
ω = S/R2
Единицей измерения телесного угла является стерадиан (пространственный радиан) ср - угол, вырезающий единичную площадь на сфере единичного радиуса. Очевидно, что телесный угол, охватывающий все пространство вокруг источника света, равен: ω = 4π.
По логике построения фотометрии, в качестве основной единицы надо было выбрать единицу светового потока. Но исторически сложилось в качестве основной единицы использовать единицы силы света. Первоначально эта единица - 1 свеча - определялась, как определенная часть силы света эталонной лампы. В настоящее время единицей силы света в СИ является кандела (Кд).
Кандела - это сила света, испускаемого с поверхности площадью 1/600000 м2 полного излучателя в перпендикулярном направлении при температуре излучателя, равной температуре затвердевания платины, под давлением 101325 Па.
Единицей светового потока в СИ является люмен (лм). Один люмен - световой поток, испускаемый точечным источником силой света 1 Кд внутри телесного угла 1 ср: 1лм = 1Кд*1ср
Для количественной оценки освещения поверхностей вводится понятие освещенности. Освещенностью поверхности называется величина, измеряемая световым потоком, падающим на единицу этой поверхности.
E = dФ/dS
Если освещенность всех точек одинакова, то Е = Ф / S, где Ф - световой поток, равномерно распределенный по поверхности S. Единица освещенности в СИ называется люксом (лк). Один люкс — освещенность поверхности световым потоком 1 лм, равномерно распределенным по площади 1 м2.
Иногда применяется единица освещенности один фот - освещенность поверхности световым потоком 1 лм, равномерно распределенный по площади 1 см2.
1 лк = 1 лм / 1 м2 =1 лм / 10000 см2 = 10-4 фот.
Первый закон освещенности:
Освещенность точечным источником поверхности, нормально падающими лучами, прямо пропорциональна силе света источника и обратно пропорциональна квадрату расстояния от источника до освещаемой поверхности.
E0 =Ф0/S0 = 4πJ/4πR2 = J/R2
Второй закон освещенности:
Освещенность поверхности наклонным световым потоком прямо пропорциональна косинусу угла падения лучей.
Е = E0cosα
Если вместо Ео во второй закон освещенности подставить его значение из первого закона, то
Е = (J / R2) cosα.
Это выражение называется объединенным законом освещенности.
До сих пор мы говорили только о точечных источниках света. Однако во многих случаях источники света являются протяженными; при рассмотрении таких источников глаз различает их форму и размеры. Для протяженных источников сила света уже не может служить достаточной характеристикой. В самом деле, из двух источников, излучающих свет одинаковой силы, но имеющих различные размеры (площади), меньший источник кажется более ярким, так как он дает большую силу света с единицы площади.
Поэтому для протяженных источников света вводится дополнительная характеристика, называемая яркостью. Яркость протяженного источника света измеряется силой света, излучаемой с единицы площади видимой поверхности этого источника в перпендикулярном направлении.
B = J/S
В системе СИ яркость измеряется в нитах (нт): 1 нт = 1 Кд / м2 . Внесистемная единица - стильб (ст): 1ст = 1 Кд / см2= 104 нт.
Фотоэффект
Влияние света на протекание электрических процессов было впервые описано Герцем (1887 г.), который заметил, что электрический разряд между заряженными цинковыми шариками значительно облегчается, если один из них осветить ультрафиолетовым светом. Дальнейшее подробное изучение влияния света на заряженные тела было проведено в период с 1888 по 1890 г. профессором Московского университета А.Г. Столетовым. Это явление он назвал актиноэлектрическим. В настоящее время оно называется фотоэффектом.
Фотоэффектом называется освобождение (полное или частичное) электронов от связей с атомами и молекулами вещества под воздействием различного вида излучений.
Если электроны выходят за пределы освещаемого вещества (полное освобождение), то фотоэффект называется внешним. Если же электроны теряют связь только со своими атомами и молекулами, но остаются внутри освещаемого вещества, увеличивая тем самым электропроводность, то фотоэффект называется внутренним. Внешний фотоэффект наблюдается у металлов, а внутренний чаще всего у полупроводников. Экспериментальные исследования, выполненные А.Г. Столетовым, а так же другими учеными, привели к установлению следующих основных законов внешнего фотоэффекта.
I закон: Фототок насыщения J (т.е. максимальное число электронов, освобождаемых светом в 1с) прямо пропорционален световому потоку Ф.
J = kФ
где k - коэффициент пропорциональности, называемый фоточувствительностью освещаемой поверхности и измеряется мкА / лм.
II закон: Скорость фотоэлектронов пропорционально возрастает с увеличением частоты падающего света и не зависит от его интенсивности.
III закон: Независимо от интенсивности света, фотоэффект начинается только при определенной (для данного металла) минимальной частоте света или максимальной длине волны, называемой красной границей фотоэффекта.
Законы внешнего фотоэффекта получают простое истолкование на основе квантовой теории света. По этой теории, величина светового потока определяется числом световых квантов (фотонов), падающих в единицу времени на поверхность металла. Каждый фотон может взаимодействовать только с одним электроном. Поэтому максимальное число фотоэлектронов должно быть пропорционально световому потоку (первый закон фотоэффекта). Энергия фотона hv, поглощенная электроном, частично расходуется на совершение работы выхода электрона из металла А; оставшаяся часть этой энергии идет на сообщение ему кинетической энергии mυ2/2. Тогда, согласно закону сохранения энергии, можно записать:
hv = A + (mυ2)/2
Эта формула, предложенная в 1905 году Эйнштейном и подтвержденная затем многочисленными экспериментами, называется уравнением Эйнштейна. Из этого уравнения непосредственно видно, что скорость фотоэлектрона возрастает с увеличением частоты света и не зависит от его интенсивности (поскольку ни А, ни v не зависят от интенсивности света). Этот вывод соответствует второму закону фотоэффекта. Кроме того, из уравнения Эйнштейна следует, что с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается (величина А постоянна для данного освещаемого металла). При некоторой достаточно малой частоте v = vmin (или длине волны λmax= с / vmin) кинетическая энергия фотоэлектрона станет равной нулю (mυ2)/2= 0 и фотоэффект прекратится (третий закон фотоэффекта). Это будет иметь место при hvmin = A, т.е. в случае, когда вся энергия фотона расходуется на совершение работы выхода электрона. Тогда: vmin = A/h, или λmax = hc/A
Эти формулы определяют красную границу фотоэффекта и что она зависит от величины работы выхода, т.е. от рода металла. На внешнем фотоэффекте основан важный физико-технический прибор, называемый вакуумным фотоэлементом. Катодом К служит слой металла, нанесенный на внутреннюю поверхность стеклянного баллона, из которого выкачан воздух. Анод А выполнен в виде металлического кольца, помещенного в центральной части баллона. При освещении катода, в цепи фотоэлемента возникает электрический ток за счет электронов, выбитых из катода. Сила тока пропорциональна величине светового потока, падающего на катод. Большинство современных фотоэлементов имеют сурьмяно-цезиевые или кислородно-цезиевые катоды, обладающие высокой фоточувствительностью. Первые чувствительны к видимому и ультрафиолетовому свету, а вторые к инфракрасному и видимому свету. В некоторых случаях, для увеличения чувствительности фотоэлемента, его наполняют аргоном при давлении порядка 10-2 мм.рт.ст. Фототок в таком фотоэлементе усиливается вследствие ионизации аргона, вызванной столкновением фотоэлектронов с атомами аргона. Внутренний фотоэффект наблюдается у полупроводников и, в меньшей мере, у диэлектриков. Полупроводниковая пластинка присоединяется к полюсам батареи. Ток в цепи незначителен, поскольку полупроводник обладает большим сопротивлением. Однако при освещении пластинки ток в цепи резко возрастает. Это обусловлено тем, что свет вырывает электроны из атомов полупроводника, которые, оставаясь внутри полупроводника, увеличивают его электропроводность. Такое сопротивление называют фоторезистор. На явлении внутреннего фотоэффекта основана работа полупроводниковых фотоэлементов. Для их изготовления используют селен, сернистый свинец, сернистый кадмий и некоторые другие полупроводники. Фоточувствительность полупроводниковых фотоэлементов в сотни раз превышает фоточувствительность вакуумных фотоэлементов. Некоторые фотоэлементы обладают отчетливо выраженной спектральной чувствительностью. У селенового фотоэлемента спектральная чувствительность очень близка к спектральной чувствительности человеческого глаза. Недостатком полупроводниковых фотоэлементов является их заметная инерционность: изменение фототока запаздывает относительно изменения освещенности фотоэлемента. Поэтому полупроводниковые фотоэлементы не пригодны для регистрации быстроизменяющихся световых потоков. В качестве примера полупроводникового фотоэлемента рассмотрим устройство селенового вентильного фотоэлемента.
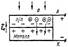Он состоит из металлической подложки, дырочного полупроводника, покрытого прозрачным слоем металла (обычно тонкий слой золота). На границе металл-полупроводник, вследствие диффузии, возникает контактный запирающий слой с напряженностью Ек. Включим теперь световой поток Ф, проникающий в полупроводник. Благодаря внутреннему фотоэффекту увеличивается концентрация свободных зарядов обоих знаков - электронов и дырок. Электроны свободно диффундируют через контакт, а для дырок он действительно является запирающим слоем. В результате при освещении электроны накапливаются на подложке, а дырки - в полупроводнике. Между контактами А и К возникает разность потенциалов
- фото-э.д.с, величина которой пропорциональна освещенности проводника. Таким образом, вентильный фотоэлемент представляет собой генератор тока, непосредственно преобразующий световую энергию в электрическую. В качестве полупроводников в вентильном фотоэлементе используют селен, закись меди, сернистый таллий, германий, кремний. В вентильном фотоэлементе могут применяться два полупроводника с различными типами проводимости - электронной и дырочной. Весьма перспективным является практическое использование вентильных фотоэлементов в качестве генераторов электроэнергии. Батареи кремниевых фотоэлементов, получивших название солнечных батарей, применяются на космических спутниках и кораблях для питания различной электронной аппаратуры. Некоторые вентильные
фотоэлементы чувствительны к инфракрасному излучению, их применяют для обнаружения нагретых невидимых тел, т.е. как бы расширяют возможности зрения. Исключительно велико значение фотоэлементов для телемеханизации и автоматизации производственных процессов. В сочетании с электронным усилителем и реле, фотоэлемент является неотъемлемой частью автоматических устройств, которые, реагируя на световые сигналы, управляют работой различных промышленных и сельскохозяйственных установок и транспортных механизмов. На внешнем фотоэффекте основана работа электронно-оптического преобразователя (ЭОП), предназначенного для преобразования изображения из одной области спектра в другую, а также для усиления яркости изображений. В медицине ЭОП применяют для усиления яркости рентгеновского изображения, это позволяет значительно уменьшить дозу облучения человека. Если сигнал с ЭОП подать в виде развертки на телевизионную систему, то на экране телевизора можно получить "тепловое" изображение предметов. Части тела, имеющие разные температуры, различаются на экране либо цветом, при цветном изображении, либо светом, если изображение черно-белое. Такая система, называемая тепловизором, используется в термографии.
ВОЛНОВАЯ ОПТИКА
Оптика - это учение о свете. По современным представлениям свет - сложное явление, в котором сочетаются такие, казалось бы, взаимоисключающие свойства, как волновые (непрерывные), так и корпускулярные (квантовые). Корпускулярная теория света была предложена в 17 веке И. Ньютоном.
Почти одновременно с корпускулярной теорией света (1678- 1690 г.) голландский физик Гюйгенс опубликовал "Трактат о свете", в котором сформулировал основные положения волновой теории света.
В своем труде Гюйгенс дал принципы распространения волнового процесса в пространстве.
Каждая точка среды, до которой дошло световое возбуждение, сама становится источником вторичных световых волн, огибающая к которым в каждый данный момент времени является фронтом распространения световых волн. Под фронтом волны понимается геометрическое место точек, до которых дошло световое возбуждение в данный момент времени.
Позднее Френель дополнил принцип Гюйгенса:
Вторичные световые волны, интерферируя между собой, взаимно гасятся во всех направлениях, кроме первоначального направления распространения волны.
Эти два положения получили название принципа Гюйгенса - Френеля. Этим объясняется прямолинейность распространения света. Свет от точечного источника распространяется в виде сферической волны. Если источник света находится на достаточно большом расстоянии, то фронт волны можно считать плоским, это предельный случай сферической волны. Волновая природа света подтверждается такими явлениями, как интерференция, дифракция и поляризация. Теория интерференции была разработана Френелем.
Интерференция света — это явление перераспределения энергии световых волн в пространстве, при наложении двух или более волновых процессов, имеющих одинаковую частоту и постоянную во времени разность фаз.
Источники света, имеющие одинаковую частоту и постоянную во времени разность фаз, называются когерентными. Пусть имеются два когерентных источника света, в которых колебания совершаются по закону s = A sin ωt.
В точке С колебания, распространяющиеся от источника S1, будут совершаться по закону:
s1 = A sin (ω t - 2πx1/λ),
а от источника S2 по закону:
s2 = A sin (ωt -2πx2/λ).
Так как волны приходят в точку С одновременно, результирующее смещение будет в любой момент определяться суммой составляющих смещений: S = S1 + S2 S = A sin (ωt - 2πx1/λ) + A sin (ωt -2πx2/λ). Применяя формулу суммы синусов, получим:
S = 2 A cos[ π(х2 — х1) /λ] sin[ωt — π (х2+ х1)/ λ ].
В этом уравнении выражение х2 – х1 = ∆ х называют геометрической разностью хода волн - это разность расстояний, которые проходят волны до встречи в точке С. Выражение 2Acos (π∆х/λ) = А' является амплитудой результирующего колебания. Подставляя различные значения Ах в формулу А', были выявлены следующие закономерности: Если геометрическая разность хода волн равна четному числу полудлин волн, то амплитуда результирующего колебания будет наибольшей - в данной точке усиление колебаний.
∆x = (2kλ)/2
Если геометрическая разность хода волн равна нечетному числу полудлин волн, то амплитуда результирующих колебаний будет минимальной - ослабление колебаний.
∆x = (2k+1)λ/2
В формулах k - натуральный ряд чисел 0,1,2,3...
При когерентных источниках волн пространство, окружающее источники, будет представляться в виде совокупности максимумов и минимумов. Такое расположение называется устойчивой интерференционной картиной. Поскольку свет представляет собой электромагнитные волны, должна наблюдаться интерференция света. Однако в результате того, что отдельные световые импульсы, посылаемые высвечивающимися атомами источника света, не согласованы между собой по фазе, а кроме того, могут отличаться по частоте, картина взаимного усиления, возникающая в каком-либо участке пространства, уже через доли секунды сменяется картиной взаимного ослабления и наоборот. Хаотическая смена таких мгновенных картин глазом не воспринимается, а создает ощущение ровного потока света, не изменяющегося во времени.
Для наблюдения устойчивой во времени интерференционной картины необходимы условия, при которых частоты и разности фаз интерферирующих лучей были бы постоянными в течение всего времени наблюдения. В природе не существует когерентных источников света. Для того чтобы два светящихся тела являлись когерентными источниками, волны, излучаемые всеми частицами первого тела, должны отличаться по фазе от волн, излучаемых всеми частицами второго тела, все время на одну и туже величину. Такое событие практически совершенно невероятно. Поэтому, для получения когерентных источников прибегают к искусственному приему: "раздваивают" свет, исходящий от одного источника (зеркала или бипризма Френеля, зеркало Лойда, билинза Билле и др.). Пожалуй, единственным макроисточником света, в котором частота и фазы колебаний со временем не меняются, является лазер.
В естественных условиях образование когерентных волн и явление интерференции можно наблюдать при попадании света на тонкую прозрачную пластинку или пленку. Пучок света попадает на тонкую пластинку. Луч 1 из этого пучка попадает на точку А, частично отражается (луч 2), частично преломляется (луч АВ). Преломленный луч испытывает отражение на нижней границе пластинки в точке В. Отраженный луч, преломившись в точке С, выходит в первую среду (луч 3). Лучи 2 и 3 образованны от одного луча, поэтому они когерентны и будут интерферировать, создавая устойчивую интерференционную картину.
При освещении этой пластинки или пленки белым светом возникает весьма причудливая по форме и расцветке интерференционная картина. Такую картину дают мыльные пленки, нефтяные и масляные пятна на поверхности воды, крылья мелких насекомых, жировые налеты на стекле и другие тонкие пленки толщиной порядка 10-4см. Это интерференционное явление широко используется в оптической промышленности для так называемого просветления оптики. Дело в том, что в сложных оптических системах (фотообъективах и т.п.) значительная часть световой энергии отражается от поверхности линз. Это заметно снижает яркость и контрастность изображения и создает блики. Если на поверхность линз нанести прозрачную пленку толщиной "к/4п, изготовленную из вещества с показателем преломления п, немного меньшим показателя стекла линз, то такая пленка не будет отражать света; благодаря этому качество изображения заметно улучшится (оптика просветлеет). Кроме того, интерференцию света используют в специальных приборах — интерферометрах — для измерения с высокой степенью точности длин волн, небольших расстояний, показателей преломления веществ и определения качества оптических поверхностей.
Дифракция — явление отклонения света от прямолинейного распространения и захождение в область геометрической тени.
В результате происходит сложение волн и образование минимумов и максимумов, так же как и при интерференции. Для наблюдения явления дифракции необходимо, чтобы размеры препятствия или размеры отверстия или щели были соизмеримы с длиной световой волны. Явление дифракции можно объяснить, используя принцип Гюйгенса — Френеля. Пусть на щель, размеры которой соизмеримы с длиной световой волны, падают световые волны. Каждая точка щели становится новым источником вторичных волн. Краевые точки щели, являясь источниками вторичных световых волн, дают возможность распространяться свету в направлении, отличном от первоначального.
Вторичные волны, интерферируя, образуют на экране дифракционные максимумы и минимумы.
От одной щели свет дает дифракционную картину малой интенсивности, поэтому используют одномоментно несколько отверстий, т.е. дифракционную решетку.
Дифракционная решетка — это совокупность многих параллельных щелей, разделенных непрозрачными промежутками. Общая длина щели и непрозрачного промежутка называется периодом решетки (d).
Дифракционную решетку можно получить, нанося на стеклянную пластинку параллельные штрихи с помощью алмазного резца. Хорошие дифракционные решетки имеют до 1000 и более штрихов на 1 мм, что позволяет получить большие углы дифракции, т.е. широкую дифракционную картину большой интенсивности. Рассмотрим дифракцию света от двух щелей при условии перпендикулярного падения света на них.
В этом случае фронт световой волны достигает щелей одновременно. Следовательно, образующиеся от щелей вторичные волны, являются когерентными. Волны, идущие по различным направлениям, будут интерферировать, давая дифракционную картину максимумов и минимумов. Выберем два параллельных луча (АА1) и (ВВ1), отклоненные от первоначального направления на угол а. Этот угол называется углом дифракции. Эти лучи, пройдя линзу, соберутся в ее фокальной плоскости (F) в точке О1, ослабив или усилив друг друга, причем АО1 = х1, ВО1 = х2. Пусть в точке О1 будет максимум колебаний. Тогда по условию максимумов ∆х = kλ (1). Выразим эту разность хода лучей из геометрии построения. Проведем перпендикуляр АС, построив тем самым фронт волны отклоненных лучей АА1 и ВВ1. Т.к. линза не вносит добавочной разности хода этих лучей, то ∆х = ВС и ВС = АВ sin?BAC. AB = d - период дифракционной решетки, угол ВАС = α, ∆х = dsin α (2).
Сравнивая (1) и (2), получим
kλ = dsinα
это уравнение дифракционной решетки, к = 0,±1, ±2, ±3... — порядок дифракционного максимума. Т.о. в фокальной плоскости возникает ряд чередующихся максимумов и минимумов, т.е. светлых и темных полос, разделенных промежутками. Если на решетку падает белый свет, то для различных длин волн положение дифракционных максимумов будет располагаться под различным дифракционным углом. Поэтому дифракционные решетки разлагают белый свет в дифракционный спектр и употребляются как дисперсионный прибор. С помощью дифракционной решетки, зная период решетки и определив угол дифракции, можно измерить длину световой волны по формуле:
λ =(d sinα)/k
Разрешающая способность оптических систем
Явление дифракции объясняет пределы разрешения и разрешающую способность оптических систем, в частности приборов для микроскопии. Объективы современных микроскопов являются сложными оптическими системами, состоящими из нескольких линз. Однако увеличение дает только одна линза, которую называют фронтальной. Обычно, это плосковыпуклая линза, стоящая первой к объекту. Остальные линзы предназначены для коррекции, т.е. устранения недостатков изображения. Увеличение объектива определяется как: Го6= ∆ / Fo6 где ∆ - оптическая длина микроскопа - расстояние между задним фокусом объектива и передним фокусом окуляра. Оптическая сила фронтальной линзы равна: D = (n - 1) / R, где n-показатель преломления вещества, из которого изготовлена линза, R-радиус кривизны поверхности фронтальной линзы.
Тогда Fo6= I/ D = R / (n - 1); Го6= ∆ (n - 1) / R
Анализируя эту формулу, кажется, что, уменьшая радиус фронтальной линзы (R0O), можно получить сколь угодно большое увеличение объектива микроскопа. Однако в действительности, уменьшение радиуса фронтальной линзы, позволяет рассматривать предметы величиной, не меньше некоторого предела, который называют пределом разрешения микроскопа.
Предел разрешения микроскопа (Z) - это наименьшее расстояние между двумя точками объекта, которые еще видны в микроскопе раздельно. Величина, обратная пределу разрешения, называется разрешающей способностью микроскопа.
Разрешающая способность микроскопа - это его возможность давать раздельное изображение двух близко расположенных точек объекта.
Чтобы определить величину предела разрешения, выясним механизм получения изображения в объективе.
В качестве объекта возьмем дифракционную решетку. Рассматривание мелких предметов в микроскопе в проходящем свете, можно уподобить прохождению света через дифракционную решетку. Самой мелкой деталью дифракционной решетки является ее период (d). Свет, проходя решетку, создает картину дифракционных максимумов и минимумов в фокальной плоскости фронтальной линзы, что и является первичным изображением. После этого, лучи интерферируют, создавая в плоскости экрана вторичную картину, т.е. изображение дифракционной решетки.
Немецкий ученый-физик Эрнест Аббе - профессор теоретической физики Иенского университета в 1872 году дал теорию образования изображения в микроскопе. Он установил: Предельным условием получения изображения является то, чтобы в его построении участвовали нулевой и два первых максимума, если свет падает перпендикулярно на предмет, или нулевой и один из первых максимумов, если свет падает под углом.
При дальнейшем увеличении числа дифракционных максимумов, будет улучшаться только четкость и яркость изображения. Чем меньше предмет или его деталь (d), тем больше углы дифракции и тем шире должно быть отверстие объектива. Отверстие объектива определяется углом между лучами, приходящими от предмета к краям фронтальной линзы. Он называется отверстным углом 2U. Половина этого угла называется апертурой U. Если апертура меньше угла дифракции, соответствующего максимумам первого порядка, то изображения предмета не будет, хотя экран станет равномерно освещен лучами нулевого дифракционного максимума. Таким образом, радиус кривизны фронтальной линзы можно увеличивать до тех пор, пока апертура объектива не станет меньше угла дифракции лучей, дающих максимумы первого порядка. Тогда: k = 1, a ~ U, sin U = λ/ d, dmin ≤ λ/ sin U, dmin = Z
Z = λ/sinU
Чем меньше предел разрешения, тем более мелкие детали объекта можно рассматривать в микроскоп, т.е. тем больше будет его разрешающая способность.
