Пусть проводится n независимых испытаний, в каждом из которых событие А может появиться или не появиться, вероятность появления А в каждом опыте постоянна и равна р (схема Бернулли).
Зададим СВ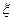 
- число появлений события А в n испытаниях.
Значения СВ 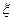могут быть – 0, 1. …, 
. Соответсвующие вероятности - Р(k)=Cnkpkqn-k
| хi | … | 
| … |
| ||
| Pi | qn | npqn-1 | … | Cnkpkqn-k | … | pn |
Дискретная СВ имеет биномиальное распределение, если она принимает значения, равные числу появлений события А в независимых испытаниях и соответствующие вероятности, определенные формулой Бернулли.
Название –биномиальное: вероятность определяется как разложение в бином Ньютона: (a+b)n=an+nan-1b+…+bn= 
Проверим, 
?
<
VМонета брошена 2 раза. Найти закон распределения и построить функцию распределения СВ 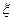–количества выпадений герба.
Ï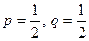 
, 
.
| хi | |||
| Pi |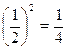 
| 
|
|
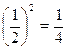
N
