Рассмотрим элементарный V вещества в форме прямоугольного параллелепипеда в декартовой системе координат.
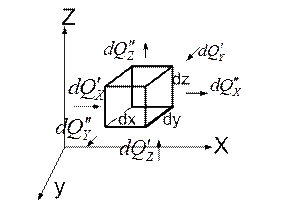
Количество теплоты, входящее через левую грань параллелепипеда в направлении оси Х, равно:
dQx΄ = q x΄dy*dz*dτ (Дж), где q x΄, Вт/м2 – удельный тепловой поток, пронизывающий левую грань. Через правую грань в этом же направлении уходит количество теплоты, равное: dQx΄΄ = q x΄΄dy*dz*dτ (Дж), где q x΄΄ - удельный тепловой поток на правой грани. Представим q x΄ через q x΄΄:
Для этого используем формулу разложения в ряд Тейлора:
q x΄΄ = q x΄ + (∂ q x΄ /∂х)*(dх/1!) + (∂2 q x΄ /∂х)*(dx2/2!) + …+ (∂nq x΄/∂xn)*(dxn/n!)
В правой части данного разложения в ряд оставляют 2 первые величины, а малые более высоких порядков отбрасывают. Количество теплоты, остающееся в параллелепипеде вследствие различия втекающего и вытекающего потоков равно: dQx = dQx΄ - dQx΄΄ = q x΄dy*dz*dτ - q x΄΄dy*dz*dτ = (q x΄ - q x΄΄)* dy*dz*dτ = -(dq x/dx)*dx* dy*dz*dτ
Используя закон Фурье выразим удельный тепловой поток в виде: q x = - λ*dt/dx и подставим эту величину в выражение: dQx = - (d/dx)*(- λ*dt/dx)*dV* dτ; dV = dx*dy*dz. При λ =const (линейная постановка). dQx = (λ*d2t/dx2)*dV*dτ. Для координат направлений у и z используем аналогичные выражения: dQу = (λ*d2t/dу2)*dV*dτ; dQz = (λ*d2t/dz2)*dV*dτ. Общее количество теплоты,поступившее в данный элементарный V: dQ = dQx + dQу + dQz= λ (∂2t/∂x2 + ∂2t/∂y2 + ∂2t/∂z2)*dV*dτ.
Считая, что вещество обладает реальной (Дж) теплоёмкостью можно выразить это же самое количество теплоты, используя значения теплоёмкости и величины нагрева: dQ = с*ρ*dV*dt =с*ρ*dV*(∂t/∂τ)*∂τ. Приравнивая теплоту из двух последних выражений получим:
λ (∂2t/∂x2 + ∂2t/∂y2 + ∂2t/∂z2)*dV*dτ = с*ρ*dV*(∂t/∂τ)*∂τ;
∂2t/∂x2 + ∂2t/∂y2 + ∂2t/∂z2=▼2;
∂t/∂τ =[ λ/ (с*ρ)] *▼2 * t.
Величина λ/ (с*ρ) = а, м2/с называется коэффициентом температуропроводности. Коэффициент температуропроводности один из важнейших коэффициентов теории теплопроводности, от него зависит скорость изменения температурного поля. ∂t/∂τ = а *▼2 * t.
Если внутри изучаемого тела имеются внутренние источники тепловыделения, то дифференциальное уравнение теплопроводности примет вид: ∂t/∂τ = а *▼2 * t + qv/(c* ρ); qv – плотность источников тепловыделения (объёмная) [Вт/м3]. Дифференциальное уравнение, приведённое выше, относится к неподвижной твёрдой среде, для движущейся среды это уравнение примет вид:
∂t/∂τ + Wx*∂t/∂x + Wy*∂t/∂y + Wz*∂t/∂z = а *▼2 * t -конвективная составляющая дифференциального уравнения теплопроводности. Wx,Wy,Wz – проекции скорости на оси.
Дифференциальное уравнение теплопроводности является уравнением энергии, так как получено на основе закона сохранения энергии.






