Потери напора по длине

При движении жидкости по трубопроводам действуют гидравличе­ские сопротивления, приводящие к потерям напора:

где h_l – потери на трение жидкости по длине трубопровода; h_м – потери на преодоление местных сопротивлений.

Потери напора по длине трубопровода при ламинарном режиме течения жидкости в круглоцилиндрическом трубопроводе были исследованы доктором медицины Ж. Пуазейлем, нашедшим следующую зависи­мость:

,

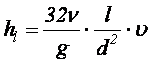где n – кинематическая вязкость жидкости;l и d – длина и диаметр трубопровода;u – скорость движения жидкости.

Преобразуем выражение (96), умножив числитель и знаменатель правой части на 2u. Получим формулу Дарси-Вейсбаха:

.

где l – безразмерный гидравлический коэффициент трения:

При ламинарном режиме движения жидкости гидравлический ко­эффициент трения X является функцией числа Рейнольдса l = f(Re_d) и пря­мо пропорционален скорости. Формула (98) справедлива также для турбу­лентного режима движения жидкости. При этом режиме течения жидко­сти коэффициент X зависит не только и не столько от числа Рейнольда, сколько от размеров и формы неровностей на внутренней поверхности труб. Для расчетов "вводят понятие об эквивалентной шероховатости К_э, мм, которая представляет собой условную форму шероховатости, размеры которой так же влияют на характер движения жидкости в трубе, как и ре­альные неровности в ней.

Толщина тонкого ламинарного слоя у внутренней поверхности труб при турбулентном режиме течения жидкости увеличивается при умень­шении числа Рейнольдса. Если число Рейнольдса таково, что толщина ла­минарного слоя больше высоты выступов на внутренней поверхности стенки труб, то такие трубы принято называть гидравлически гладкими. Толщину ламинарного слоя 5 в гидравлически гладких трубах круглого сечения при Re_d < 10⁵ можно подсчитать по следующей эмпирической формуле:

где d – внутренний диаметр трубы.

Значение 8 достигает всего нескольких долей миллиметра. У гидравлических гладких стенок по мере увеличения числа Рейнольдса все тоньше становится ламинарный слой и в большей мере проявляется их шероховатость, выступы, которые раньше полностью располагались в ламинарном слое, начинают выступать в турбулентную зону. Следовательно, одна и та же стенка в зависимости от числа Рейнольдса Re_d может в одном случае гидравлически гладкой, в другом – шероховатой. Одни и те же размеры шероховатости оказывают большее влияние на характер течения жидкости в потоках малых поперечных размеров, чем в потоках с большими сечениями. Поэтому для характеристики влияния шероховатости на гидравлическое сопротивление в гидравлике введено понятие относительная шероховатость K_э/d. Обратную величину d/К_э называют относительной гладкостью поверхности, таким образом, коэффициент гидравлического трения lдля турбулентного режима в общем слу­чае является функцией числа Рейнольдса и относительной гладкости по­верхности: l = f(Re_d, d/K_э).

При практических расчетах, определяя коэффициент X гидравлического трения при турбулентном режиме движения жидкости, используют различные эмпирические и полуэмпирические формулы, так, для гидравлически гладких труб при 4×10³ < Re_d < 10⁵ коэффициент lопределяют по формуле Блазиуса:

.

В переходной области при 10 < Re_d < 9,2×10⁵lопределяют по формуле Альтшуля:

которая для области квадратичного закона сопротивления при Re_d > 9,2×10⁵ приводится к формуле Шифринсона:

.

Из формулы (97) следует, что гидравлический уклон

.

Но согласно (57) скорость движения жидкости в трубе

где Q – расход жидкости в этой трубе;

А – площадь поперечного сечения трубы, равная A=7id²/4. Подставив в (103) значение скорости v, выраженной через Q и d, получим

.

Следовательно, гидравлические потери напора существенно зависят от расхода (прямо пропорциональны Q²) и от диаметра трубы (обратно пропорциональны d⁵).

28. Местные потери

Потери, связанные с преодолением местных сопротивлений, вызы­ваются резким изменением скорости вследствие внезапного расширения или сужения живого сечения, изменением направления движения потока и т.п. При решении практических задач потери напора на местных сопро­тивлениях определяют по формуле Вейсбаха:

,

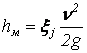где x_j – безразмерный коэффициент местного сопротивления, зависящий в основном от формы местного сопротивления и иногда от числа Рейнольдса, обычно определяется опытным путем, значения его приводятся в спра­вочниках по гидравлике.

Из выражения (106)следует, что потери напора на преодоление ме­стных сопротивлений также существенно зависят от скорости движения (прямо пропорциональны v², а следовательно, и Q²) жидкости по этому сопротивлению.