Решение задачи Лагранжа

Задача Лагранжа в классическом ее понимании заключается в следующем.

В цилиндре, ограниченном слева неподвижной стенкой и безгранично продолженном вправо на расстоянии l₀ от дна цилиндра находится поршень весом q. Площадь поперечного сечения цилиндра равна S₀. В пространстве между дном цилиндра и поршнем находится кг газа под давлением p₀ с плотностью ₀. Газ однороден и неподвижен. В момент t = 0 поршень получает возможность двигаться без сопротивления под действием давления газа. Движение газа является одномерным, влияние теплоотдачи не учитывается. Требуется определить возможное в этих условиях движение газа и движение поршня. Таким образом задача Лагранжа сводится к основной задачи внутренней баллистики в предположении о мгновенном сгорании заряда и отсутствии теплоотдачи сопротивления движению и других второстепенных работ, за исключением движения газа. Задача поставленная в 1790г. неоднократно привлекала к себе внимание многих ученых: Пиддек (1921г.), Госсо и Лиувиль(1922г.), Фок(1935г.), Платрие (1936г.)-вот далеко не полный перечень ученых, посветивших свои работы решению этой задачи. Наиболее полно она решена С.А. Бетехтиным (1948г.) с учетом коволюма газа для каморы с уширением, с учетом теплоотдачи. Позднее она решалась Л.Л. Поповым, Зайченко Ю.И. (в оссиметричной постановке), Никулиным О.А. в новых относительных переменных, Ушаковым В.М., Комаровским А.В. и другими.

Решение задачи Лагранжа имеет большое практическое значение, т.к. позволяет установить основные закономерности движения газов и в более сложных случаях, каким является течение газопороховой смеси при выстреле из орудия.

С газодинамической точки зрения задача Лагранжа является задачей об одномерном неустановившемся движении газа при соответствующих начальных и граничных условиях. Если поместить начало координат у дна цилиндра и направить ось X в сторону движения поршня, то начальными условиями будут следующие: при t =0 0=<x<l₀, Р=Р₀, , U=0, T=T₀.

Граничные условия вытекают из того обстоятельства, что слои газа непосредственно прилегающие к дну цилиндра и к дну поршня не могут ни проникнуть через эту поверхность, ни отставать от них. По этому граничные условия будут формулироваться следующим образом:

X=0, U=0

X=l+l₀, (11,14)

где l - путь, пройденный поршнем к рассматриваемому моменту времени.

Допустим, что газ идеальный. Рассмотрим область движения в плоскости X,t. Слева она ограничена осью t, а справа - неизвестной еще нам кривой, изображающей закон движения поршня X=f(t). Начальными условиями определены все искомые функции на отрезке 0 - l0 оси X. Известно, что f'(0)=0, f''(0)>0, f''(t)>0, т.е. поршень начинает двигаться с нулевой скоростью, но с конечным ускорением, причем ускорение поршня остается положительным во время его движения. Поскольку слой газа, примыкающий к дну поршня не может ни оторваться, ни обогнать поршень в своем движении, будет всегда выполняться условие:

Ux=f(t)=f'(t)

где Ux=f(t) - скорость слоев газов, прилегающих к дну поршня. Таким образом скорость, а следовательно и остальные параметры переднего слоя будут непрерывно изменяться в результате движения поршня.

Расширение бесконечно тонкого газа будут вызывать расширение соседнего слоя газа, а это в свою очередь приведет к последовательному расширению все более и более удаленных слоев газов. Погазу будет распостраняться волна разряжения. Поскольку поршень движется с конечным ускорением, то за бесконечно малый промежуток времени скорость, а следовательно остальные параметры газа будут изменятся на бесконечно малую величину. Но,как известно, бесконечно малые изменения параметров газа распостраняются по массе газа,т.е. передаются от слоя к слою с вполне определенной скоростью, зависящей от давления и плотности газа и носящей название местной скорости звука в газе. Если при этом сами слои газа двигаются со скоростью "U" вправо, то бесконечно малые изменения параметров газа или элементарные возмущения будут перемещаться относительно неподвижных стенок трубы по закону

(11.15), где С –скорость звука в газе (уравнение 11.15 нельзя записать в конечном виде т.к. "U" и "c" могут быть функциями "x" и"t").

Допустим,что нам удалось найти частное решение системы (11.13), т.е. отыскать такие две функции: и , которые удовлетворяют уравнениям (11.13) и граничному условию , имея это решение, мы можем построить в плоскости (x,t) систему линий

, которые называются характеристиками (рис… фиг.2).

В условиях задачи Лагранжа, линии будут прямыми, идущими расходящимися пучками, т.е. на одно элементарное возмущение не будет в процессе своего перемещения обгонять предыдущее,т.к. скорость звука падает при расширении. А так как каждое последующее элементарное возмущение распостраняется по газу, все более и более разряженному, воздействием предыдущих возмущений, то отсюда и следует, что одно последующее возмущение не сможет догнать предыдущее. Система значений U=0 и с=с₀ нетрудно убедится, также будет одним из частных решений системы U=U₁(x,t) и c=c₁(x,t) будут справедливы лишь выше линии ОА. Таким образом вдоль линии ОА происходит переход от одного частного решения системы к другому.

Как было показано выше вдоль характеристик выполняются соотношения , аналогично вдоль характеристики, идущей вправо будет выполнятся соотношение или окончательно можно записать: (11.16)

(характеристики I семейства

(11.17)

(характеристики II семейства

S и R называются инвариантами Римана.

Уравнения (11.16) и (11.17) имеют вполне определенный физический смысл. Уравнения характеристик в плоскости x, t как следует выше описывают законы перемещения элементарных возмущений. Уравнения же характеристик в плоскости искомых функций определяют связь между изменениями скорости течения "U" и местной скорости звука –"с", которая должна выполнятся при перемещении данного элементарного возмущения.

Значения "U" и "с" в любой точке области движения можно выразить через S и R в этой точке, т.е. через значения постоянных интегрирующих вдоль характеристик, противоположных семейств, проходящих через данную точку 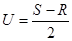, 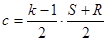(11.18)

Поскольку S или R сохраняют постоянное значение вдоль данной характеристики соответственного семейства, но могут принимать различные значения вдоль различных характеристик этого семейства, то вообще говоря возможно следующие три случая:

1. В некоторой части плоскости (x, t) S имеет на всех характеристиках I семейства одно и то же значение S=Idcm, а R=Idm. одно и то же значение на всех характеристиках II семейства в этой же части плоскости,т.е. во всех точках плоскости U=const и c=const, т.е. поток газа будет в этой части плоскости однородным. Если при этом S=R,то U=0,а с=с₀ рассматриваемая область будет областью покоя (рис…)

2. Постоянные интегрирования одного из семейств (предположим,что I семейства) сохраняет постоянное значение в некоторой области (S=Idm.) постоянные же интегрирования другого семейства (II семейства) R меняется от характеристики к характеристике. Поэтому в пределах рассматриваемой области вдоль каждой характеристики II семейства в плоскости x, t скорость течения "U" и местная скорость звука будут сохранять постоянные значения (S=Idm. R=const вдоль этой характеристики) I семейства, то сами характеристики II семейства будут прямыми линиями. Течения такого рода носят названия волн одного направления (рис..).Так как вдоль линии ОА все характеристики I семейства имеют одно и то же значение S=Idm, то в области волны одного направления характеристики II семейства будут прямыми линиями, а характеристики I семейства, где в каждой точке только S=const,а R –меняется,эти характеристики I семейства будут кривыми линиями. Характеристики I семейства –кривая АВ будет отделять область волны одного направления от области, где S, R меняться от характеристики к характеристики (область общего случая неустановившегося движения в газе).

3. Третий случай, когда в пределах рассматриваемой области оказываются переменными как S так и R это является наиболее общим случаем неустановившегося движения газа. Для этого случая нельзя установить каких-либо иных закономерностей, кроме тех, которые заложены в самих уравнениях характеристик.

В области волны одного направления параметры газа и скорость течения, а также закон движения поршня находятся по аналитическим зависимостям. В общим случае, задачи решаются численно. Если ОА разбить на 256 отрезков, то значения находятся с точностью до 0,1% в области волны одного направления, эту точность можно перенести и в общий случай. Как правило, чтобы уменьшить количество вариантов задача Лагранжа решается в относительных переменных. Обычно за отнсительные переменные принимаются:

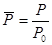, , , , , , (11.19)

Такие относительные переменные неудобны при оценке влияния коволюма газа, ускорения поршня длины ствола, уширения каморы.

В частности,в этих относительных переменных решена задача Лагранжа,С.А. Бетехтиным,Н.Н. Поповым и другими. Из результатов решения трудно выявить волновую картину процесса расширения газа.

О.А. Никулиным предложены новые относительные переменные, которые свободны от перечисленных выше недостатков.

За единицу измерения параметров принимаются: , где - аналог скорости звука в газе, равный

(11.20)

- начальное ускорение поршня (11.21)

S₀ –площадь сечения канала ствола

q –вес снаряда

Р₀ –начальное (максимальное давление газа)

Т₀ –начальная температура(max)

R –газовая постоянная

- ковалюм единицы массы газа

-начальная плотность газа (max)

K –показатель адиабаты

Тогда , , , , , , , 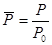(11.22)

В области волны одного направления относительные переменные определяются по следующим формулам (в зависимости от )

(11.23)

(11.24)

(11.25)

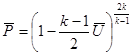(11.26)

(11.27)

(11.28) (11.29)

Уравнение справедливо до момента т. В,когда отраженная от дна канала ствола волна догонит снаряд

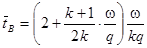(11.30)

Откуда оптимальный относительный вес газа

(11.31), т.е. когда отраженная от дна каморы волна догонит снаряд у дульного среза.

Из выражения (11.20-11.31) следует,что скорость снаряда и параметры газа , а также оптимальное значение при одних и тех же значениях и длине ствола S₀ не зависят от ковалюма газов влияет только на объём каморы, или длину каморы при S₀=const увеличивая её на величину . Численные расчеты показывают справедливость такого вывода и в более общем случае.

газ водород

Таблица 25

 

0,7881	0,1671	0,00157	0,7882	0,1671	0,0016
0,6351	0,3137	0,00650	0,6352	0,3137	0,0065
0,5242	0,4440	0,0150	0,5214	0,4440	0,0152
0,4344	0,5614	0,0276	0,4346	0,5614	0,0275
0,3668	0,6673	0,0437	0,3669	0,6669	0,0437
0,3134	0,7638	0,0641	0,3135	0,7634	0,0640
0,2704	0,8519	0,0885	0,3705	0,8519	0,0885
0,2553	0,9336	0,1172	0,2354	0,9332	0,1172
0,0881	1,1314	0,2606	0,0883	1,1311	0,2602
0,0361	1,262	0,5385	0,0361	1,2613	0,5373
0,01558	1,354	1,0472	0,0155	1,3533	1,0439
0,00689*	1,421*	1,9520*	0,0069*	1,4205*	1,9456*
0,003116	1,472	3,548	0,0031	1,4718	3,5328
0,001427	1,512	6,3531	0,0014	1,5113	6,3222

 

В таблице отмечены изменения давления на снаряд, относительная скорость снаряда и относительный путь снаряда для идеального водорода () и реального водорода (). Из таблицы видно,что коволюм не влияет на эти характеристики и так как расчеты проводились в абсолютных значениях величин, а обработка в новых относительных переменных, то видно,что точность расчета выше чем 0,1% (при сравнении с аналитическими формулами (11.20)-(11.31)).

На рис…показано изменение относительного давления от скорости снаряда, а на рис….. изменение относительной скорости от относительного пути снаряда. Из рис. 1 и 2 видно,что огибающие кривых соответствуют случаю когда ∞, точками 0.5;1.0;1.5;2.0;2.5;3.0;3.5;4.0;5.0;6.0;7.0 соответствует значению , и т.д. и они показывают:

1. при заданной относительной длине ствола , соответствует максимальной относительной скорости снаряда и оптимальное значение веса газа, т.е. и

2. Если мы увеличим количество газа , то скорость снаряда ни найоту не увеличивается,т.е. дополнительное количество газа просто не участвует в передачи энергии снаряду т.к. дополнительного слоя волна разряжения идущая от дна снаряда не успела дойти, а снаряд вылетел из ствола.

Если мы уменьшим количество газа т.е. , то получим резкое падение скорости снаряда при заданной длине ствола

Например, при , , , , ,

при и , , , то есть ни дульная скорость снаряда, ни дульное давление не увеличивалось.

Увеличилась только длина каморы в 1,5 раза. Этот вывод не был бы сделан если бы не делали пересчет при использовании прежних относительных переменных 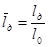, при при , которое не зависит от (это важно,при обычных относительных переменных 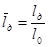увеличилась бы в 2 раза) дульная скорость , .

На рис. 3 приведены оптимальные значения для разных газов, принимая

показатель адиабаты для гелия , для водорода и пороховых газов . Уравнения (11.23),(11.26),(11.31)примут вид:

для гелия

для водорода

для пороховых газов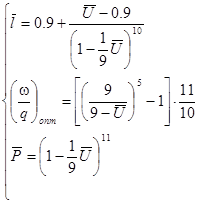

Результаты расчетов представлены в таблице 26

	5/3	7/5	11/9	5/3	7/5	11/9	5/3	7/5	11/9
0,5	0,2316	0,206	0,191	0,550	0,434	0,364	0,4996	0,4997	0,4998
1,0	2,016	1,469	1,225	1,56	1,11	0,902	0,9949	0,9956	0,9987
1,5	12,75	6,50	4,615	3,75	2,24	1,64	1,484	1,476	1,484
2,0		25,8	14,5		4,24	2,76	1,884	1,93	1,95
2,5		107,5	42,34	43,8	8,17	4,5	2,19	2,333	2,386
3,0	-	529,8	122,0	-	17,0	7,25	-	2,67	2,78
3,5			358,9			11,8			3,075
4,0						19,7			3,42

В таблице приведены результаты скорости снаряда в случае использования классического метода расчета –" термодинамического " расширения газа.

,где или окончательно

(11.32)

при одинаковых значениях и .

Из таблицы в частности видно,что при дульных скоростях снаряда для пороховых газов .

Термодинамическое расширение даёт дульную скорость на 500-600 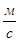ниже, а при скорости 3,5-3,8 реально получены на установках ППН для легких снарядов ().Из соотношения (11.32),найдем оптимальное значение , которое дает максимальное значение скорости при заданной длине ствола .

Дифференцируя и приравнивая , получим соотношение:

(11.33)

Разрешая это уравнение, находим .

Например. Для пороховых газов получим вместо значение при этом , т.е. 2.5% больше, что не может быть т.к. в передаче энергии снаряду участвует лишь 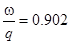или пусть получим вместо значение при этом вместо , однако количество газа участвующая в передаче энергии снаряду равно . Остальное количество газа лишнее.

11.3 Влияние уширения каморы.

Из графиков рис. 1 и 2 ясно, чтобы увеличить скорость снаряда при заданной природе газа, максимальном давлении и заданной длине ствола, необходимо длину каморы оставить без изменения, но увеличить поперечное сечение каморы,т.е. x>1, тогда большее количество газа будет участвовать в передаче энергии снаряду.

Результаты расчетов при больших значениях и резком переходе из газовой каморы l ствол приведены на рис.3.

Приближенно оценить увеличение скорости снаряда за счет уширения каморы можно по выведенным О.А. Никулиным формулам

(11.34)

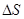увеличение инвариантно S

где "U₁", и "U" скорости газа на входе и выходе из соединительного конуса между каморой стволом.

Формула (11.34) выведена при предположении,что в переходном конусе.

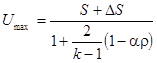(11.35)

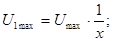
Подставляя (11.35) в уравнении (11.34) окончательно получим

(11.36)

где

Для бесконечного уширения каморы x=∞ получим

(11.37)

Результаты 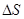полученные для водорода и гелия при и разных значениях уширения каморы приведены в таблице 27

 

Таблица 27

	водород	гелий
приближенное	точное	приближенное	точное
	0,388	0,302	0,347	0,288
	0,587	0,402	0,570	0,388
∞	0,605		0,645

Точное решение полученное при решении задачи Лагранжа с уширением каморы и 16 при нахождении точного решения радиуса переходного конуса имеем вид (11.38)

где 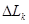-высота переходного конуса R и r радиусы каморы и ствола, соответственно. В таблице 28 приведены результаты расчетов для реального водорода () с уширением каморы x=16 и разных значениях

Таблица 28

	0,1921	0,9239	0,1358	0,0563	0,019
	0,3757	0,8232	0,238	0,1370	0,081
	0,5469	0,7180	0,260	0,2871	0,187
	0,7046	0,6212	0,3190	0,3854	0,346
	1,1032	0,3854	0,4684	0,6663	1,206
	1,6860	0,1668	0,5574	1,1286	5,03
	2,1028	0,0800	0,5889	1,5139	13,684
	2,207	0,0544	0,595	1,702	21,80
	73,065	0,0074	0,5458	2,519	144,17

Как видно из таблицы в случае реального водорода (с учетом ковалюма) значение приближается к 0,595 т.е. к вычисленной по приближенной формуле 0,587 для идеального водорода. Таим образом реально получить приращение 500-600м/с при одинаковых и максимальных давлениях используя уширение каморы x=16 или .

Этот вывод важен при проектировании пороховых и легкогазовых установок и повышения начальной скорости снаряда из боевого орудия, для получения скорости свыше 2000 м/с.

11.4 Условия постоянного давления на снаряд по всей длине ствола.

При горении пороха рассмотрим характеристику I семейства в области волны одного направления откуда

т.к. имеется зависимость получим

или

(11.39)

где используется соотношение 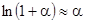при малых значениях .В случае пороховых газов ,

, т.е. ошибка равна т.е. ошибка составляет 13% в сторону занижения.(, где относительная ошибка). Рассмотрим пороховую камору большого объёма, когда количеством газа можно пренебречь, тогда

(11.40)

при получим т.к. 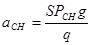, то окончательно (11.41), т.е. зная максимальное давление в каморе и давление на снаряд, которое постоянно по стволу и , легко получить марку пороха и все остальные характеристики.

,принимая

и К=11/9 получим ; при .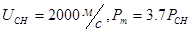

В качестве воспламенителя можно использовать любой быстро горящий порох, который выводит на заданный уровень давления на дно снаряда,т.е. порох должен быть комбинированный.

 

12.Пороховые и легко газовые установки.

Пороховые и легко газовые установки нашли широкое применение при гиперзвуковых исследованиях.

Пороховые установки рис. 55 как и орудие имеет ствол, пороховую камору и затвор. В пороховых установках ППН, созданных под руководством О.А. Никулина: на ствол, навинчивался пороховой стакан, представляющий собой толстостенную болванку со сплошным дном. В болванке имеется камора с уширением x=3,6 переходящая в цилиндр диаметром равным диаметру канала ствола. В ствол помещалось метаемое тело в поддоне. Иногда между стволом и пороховым стаканом помещалась мембрана со специальной насечкой для увеличения давления форсирования снаряда. В дне болванки имелось отверстие, через которое вставлялся инициирующее устройство в камору. Ствол со стаканом размещался на легкой раме. При выстреле установка отскакивала назад. Калибры ствола 23;34;50. Длина ствола 70-80клб. Давление в каморе 10000-15000кг/см². Скорости,полученные на установках со снарядом С_q=1,0-2,0кг/дм³ были 3000-2600 м/с соответственно.

На установках использовались штатные пороха. Были проведены специальные стрельбы по выяснению влияния различных фактов влияющих на баллистику выстрела, в частности применение различных добавок и основному заряду, использование комбинированных зарядов и желеобразных топлив и т.д. Проектирование установок базировалось на результатах решения задачи Лагранжа в новых относительных переменных,предложенных О.А. Никулиным. В дальнейшем установки ППН были модернизированы с увеличением объёма каморы, и её уширения до x=8-9 при этом достигнуты скорости на тех же калибрах. При решении ОЗВБ использовался газодинамический метод, разработанный профессором В.М. Ушаковом.

На установках ППН проведены несколько десятков тысяч опытов. Типичный характер изменения давления от пройденного пути снарядом представлены на рис 56 легкогазовые установки.

Как известно, максимальная возможная скорость неустановившегося течения : , которая прямо пропорционально скорости звука в газе. При одинаковой температуре газа наибольшей энергией будут обладать атомарный водород, гелий, так называемые легкие газы. Скорость звука молекулярного водорода при комнатной температуре примерно 1300м/с, выше скорости звука пороховых газов ( 1000м/с).Если нагреть легкие газы до температуры 2000-2500К, то скорость звука 3000-4000м/с, а следовательно и максимальная скорость снаряда будет значительно выше, чем она достигнута на пороховых установках. Нагреть водород или гелий можно различными способами: электрическим разрядом, ударной волной, стехиометрической смесью кислорода и водорода (геливопаровая пушка) и движущимся поршнем, который сжимает легкий газ и в процессе сжатия нагревает его до нужной температуры. Поршневые легко газовые установки оказались наиболее перспективные и на них достигнуты скорости до 12 км/с,скорости 7-8км/с являются рабочими скоростями ЛГУ, где используется деформируемый поршень. На рис.57 показано схематически ЛГУ с легким поршнем.

ЛГУ состоит из пороховой каморы поз.1, в которой размещен пороховой заряд и газовой каморы поз.4, в которую накачивается легкий газ (водород или гелий)при комнатной температуре до давления 5-30кг/см². Пороховая камора отделена от газовой поршнем, выполненного из легко деформируемого материала (полиэтилена). Газовая камера соединяется со стволом (поз.8) с помощью конического переходника (поз.5), выдерживающей высокие давления газа (8000-15000кг/см²). В ствол вставляется снаряд (поз.9), состоящей из метаемого тела, которое помещается в поддоне из легкого прочного материала, так что относительный вес снаряда С_q=1-3кг/дм³. Метаемое тело отделено от легкого газа диафрагмой (поз.10), которая раскрывается при определенном заданном давлении (давления форсирования –Р_ф). Установка работает следующим образом: при подаче электрического импульса на инициирующее устройства, устройство срабатывает и воспламеняет пороховой заряд. При достижении давления форсирования, которое больше или равно начальному давлению водорода, поршень начинает двигаться по газовой камере. По мере сгорания порохового заряда поршень двигаясь с большой скоростью сжимает легкий газ и нагревает его: создаются определенные условия по давлению и температуре. При достижении заданного давления легкого газа –Р_ф диафрагма разрывается и снаряд – метаемая сборка под действием легкого газа разгоняется по вакуумированому стволу до заданной скорости. Такая легко газовая установка называется двух ступенчатой ЛГУ с "легким " поршнем. В первую ступень входит пороховая камера и поршень. Выстрел из первой ступени подобен выстрелу из обычного орудия с противодавлению снаряду. Решение задачи внутренней баллистики первой ступени и методы идентичны ОЗВБ орудия. Здесь могут быть использованы как газодинамический, так " термодинамический " методы решения. Разделение поршней на "тяжелый " и "легкий" связано с достижением поршнем скорости больше или меньше скорости звука. При малых скоростях поршня ("тяжелый" поршень) ударной волны не образуется в легком газе и метод характеристик, изложенный выше как правило используется при решении ОЗВБ второй ступени. В случае использования "легкого " поршня газодинамический подход к решению ОЗВБ второй ступени обязательные методы "сквозного " счета, где ударная волна "размазывается " за счет введения "искусственной " вязкости газа.

Типичная картина изменения давления в пороховой и газовой камерах представлены на рис…..

Исследование внутренней баллистики ЛГУ усложняется не только за счет увеличения количества параметров, от которых зависит процесс выстрела, но и конструктивным оформлением поршня, диафрагмы, метаемой сборки, наличие конического переходника, в котором происходит торможение поршня в целом при одновременном ускорении его переднего торца за счет "гидроэффекта ". Приборы и аппаратура используемая при внутри баллистических исследованиях базируется на последних достижениях науки и техники в области быстропротекающих процессов и главное –результаты исследований, достижения в ЛГУ вполне могут быть перенесены на баллистику орудия. В этом смысле исследование в ЛГУ –это "форпост" в баллистике орудия. В доказательство этого вывода являются докторские диссертации Л.В. Комаровского, Ю.П. Хоменко, В.М. Ушакова, В.В. Жаровцева и др.