Приведенные в пиростатике зависимости и методика определения характеристик позволяет по опытам в манометрической бомбе дать полный анализ баллистических характеристик и его закона горения.
Баллистические характеристики: сила пороха f и коволюм 
определяются по опытам в бомбе при 2-х – 3-х плотностях заряжания по 3-5 опытов при каждой 
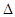. В полученные на опыте данные (pm, f, ) вводится поправка на теплоотдачу и определяются исправленные значения f0 и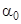 
, коэффициент скорости горения – U1 определяется на основе обработки интегральной кривой 
, 
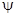. Геометрический закон горения пороха позволяет определить газоприход, быстроту газообразования, интенсивность газообразования чисто из геометрических соотношений.
Физический закон горения характеризуется опытной кривой интенсивности газообразования 
в функции от 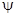или t и кривой изменения импульса давления в функции сгоревшей части заряда 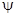. Кривая Г(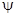) является анализатором процесса, протекающего при горении пороха в замкнутом объеме и позволяет учесть влияние различных факторов, которые другими методами обнаружить или невозможно или затруднительно. Для суждения о горении пороха в канале орудия при выстреле необходимо провести опыты в бомбе при различных плотностях заряжания и определить влияние 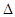на уменьшение прогрессивности горения или провести опыты в бомбе конструкции Ю.Ф. Христенко при 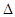, используемых в орудии. Весь этот метод исследования может быть назван методом баллистического анализа порохов. Этот метод позволяет конструировать партию готовой продукции путем сравнения опытных кривых с кривыми образцового пороха и дать заключение, что можно определить при стрельбе из орудия.
Обозначим характеристики штатного образца - 
опытного образца - 
, тогда
где 
- плотность заряжания штатного пороха в орудии. Чтобы избежеть погрешностей лучше величины J// и J/ брать как J=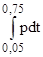 
, чтобы устранить разброс воспламенения пороха.
Приведенная формула позволяет без стрельбы определить примерный вес опытной партии пороха, дающей то же самое наибольшее давление газов и начальную скорость снаряда, что и штатный порох. Более точное значение получим, если решим основную задачу внутренней баллистики по специально разработанной программе.
РАЗДЕЛ 2.
9. Физические основы выстрела из ствольных систем.
Пироданамика изучает явления, происходящие в канале ствола при выстреле и устанавливает связь между условиями заряжания и различными физико-химическими процессами, и механическими явлениями, протекающими при этом. В явлении выстрела можно различить следующие периоды:
1-й предварительный период, когда, воспламеняясь порох горет практически при постоянном объеме. Ведущий поясок (в.п.) снаряда под действием нарастающего давления врезается в начале постепенно до тех пор, пока не войдет в.п. на полную глубину нарезов (в гладком стволе в.п. обжимается до полной величины обжатия). После чего сопративление в.п. падает и дальше снаряд движется уже с готовыми выступами на в.п. Усилие П0, необходимое для врезания в.п. в нарезы на полную глубину отнесенное к единице площади поперечного сечения канала S, т.е. 
называется давлением форсирования – p0. В зависимости от устройств в.п. и нарезов p0=250-500 кг/см2. Для пули, имеющую большую относительную площадь врезания оболочки в нарезы p0=1100-1500 кг/см2.
Таким образом в этот период входит период воспламенения пороха и период врезания в.п. в нарезы (период форсирования). Таким образом – горение пороха и воспламенителя идет в предварительном периоде от pа (атмосферное давление) до pв и далее до p0 и протекает в течении времени t0. При расчете этого периода предпологается мгновенное сгорание воспламенителя, мгновенное воспламенение всего порохового заряда и снаряд стоит на месте, пока давление пороховых газов не достигнет величины p=p0. На рис.1 это участок 0-t0.
2-й период. За предварительным периодом следует основной, или первый период выстрела, период горения и образования газов в изменяющемся объеме, когда пороховые газы, сообщая снаряду скорость, совершают работу за счет заключенной в них энергии и преодолевают ряд сопротивлений. Этот период от начала движения снаряда и до конца горения пороха, когда прекращается приток новых газов, является наиболее сложным: с одной стороны приток количества газов увеличивает давление внутри канала ствола, а, с другой стороны, непрерывное увеличение скорости снаряда и связанное с этим увеличение объема "заснарядного пространства" понижают величину давления.
В начале основного периода, когда скорость снаряда еще невелика, количество газов растет быстрее, чем объем за снарядного пространства и давление повышается, достигая максимума. Однако увеличение давления, а значит и увеличение ускорения снаряда в конечном итоге приводит к быстрому увеличению объема заснарядного пространства, и потому, несмотря на продолжающееся горение пороха и приток новых газов давление уменьшается до величины pк (точкой "к" обозначен момент сгорания порохового заряда). В этот момент скорость снаряда υк = (0,8-0,9)υд (80-90% дульной скорости). В этот период развивается наибольшее давление газов (момент обозначен временем tm) – одна из основных баллистических характеристик выстрела. Максимальное давление является основной величиной для расчета прочности ствола орудия, снаряда, взрывателя и т.д.
На рис 1. представлено изменение давления пороховых газов и нарастание скорости от t0 до tk.
3-й период. Период расширения пороховых газов (второй период). После конца горения пороха приток новых газов прекращается, но т.к. имеющиеся газы обладают большим запасом энергии, то на оставшейся части пути до дульного среза продолжают совершать работу, увеличивая скорость и энергию снаряда. Этот период представляет собой период расширения сильно сжатых и нагретых газов. Надо отметить, что оставшуюся часть пути снаряд проходит очень быстро, поэтому можно пренебречь потерями тепла через стенки ствола в процессе расширения можно считать адиабатическим. Период заканчивается моментом прохождения дна снаряда через дульный срез ствола. Давление падает от pк до pд, а скорость с υk до υд (см. рис.1 и 2). Если обозначить через:
S- площадь сечения канала ствола
p- давление газов в канале во время t
l- путь, пройденный снарядом массой m
υ- его скорость
На основании общей теоремы механики, что приращение работы, совершаемой силой равно приращению кинетической энергии будем иметь:
(9,1)
Интегрируя (9,1) получим:
Откуда υ=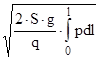 
(9, 2)
где q=mg – вес снаряда.
Выражение 
есть площадь между осью l и кривой давления p от l (см.рис.2). Кривая давления в определенном масштабе дает кривую ускорения снаряда
(9,3)
Т.к. кривая давления до максимума pm растет, то в точке m на кривой υ(t) мы будем иметь точку перегиба:
(9,4)
4 период последействия газов (третий период выстрела).
После вылета снаряда из орудия газы, вытекающие с большой скоростью вслед за снарядом продолжают на некотором расстоянии lп оказывать давление на снаряд, сообщая снаряду дополнительный импульс (- 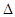(mυ)).
В конце третьего периода, когда скорость снаряда сравняется со скоростью газов, снаряд достигает наибольшей скорости:
После чего скорость снаряда начинает убывать под действием сопротивления воздуха. Помимо последействия на снаряд, газы действуют так же на ствол и учет их воздействия оказывает существенное влияние на расчет относительных частей и лафета. Последействие газов на лафет длится значительно дольше чем на снаряд (см. рис.1 и 2).
Кроме указанных выше основных процессов в эти периоды выстрела имеет место ряд побочных процессов, которые так же влияют на общий ход явлений: перемещение газов в за снарядном пространстве, откат ствола, прорыв газов через зазоры между стенками ствола и снарядом, врезание снаряда, нагрев ствола и т.д. Исходя из сказанного можно установить основные процессы выстрела и характеризующие их зависимости.
1. Источником энергии является расширяющиеся газы, которые образуются при сгорании пороха, а потому законы образования газов являются основные зависимостями, выражающими процесс горения пороха. В пиростатике установлены следующие законы:
а) образование газов, в зависимости от сгоревшей толщины пороха:
(9,5)
или 
где z=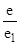 
; 
б) скорость горения U= 
(9,6)
в) быстрота газообразования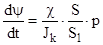 
(9,7)
При физическом законе горения используется зависимость
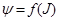
или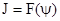 
а так же 
2. Поскольку при выстреле происходит преобразование энергии, то 1-й закон термодинамики или закон преобразования энергии даёт вторую основную зависимость 
.
Q- количество тепла, подведенного к системе из вне
U- внутренняя энергия газа
l- сумма внешних работ, произведенная газом, включая работу на преодоление вредных сопротивлений
A- механический эквивалент тепла.
3. Следующей основной зависимостью будет поступательное движение снаряда: 
(9,8)
или 
(9,9)
4.Т.к. при выстреле система заряд-снаряд приходит в движение под действием внутренних сил, то сумма количества движения равна нулю:
(9,10)
где 
- масса газа (заряд);
U – средняя скорость заряда
5. Уравнение вращательного движения снаряда
(9,11)
где r – расстояние от оси снаряда до центра боковой грани
N – сила вращения; Jz – момент инерции снаряда относительно оси вращения; 
- угловая скорость вращения
- угловое ускорение
6. Кинематическая связь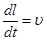 
(9,12)
9.1 Баланс энергии при выстреле.
Пусть в момент времени t имеются следующие условия: сгорела часть 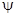заряда, снаряд весом q пролетел путь l и имеет скорость υ; температура горения пороха T1. Т.к. газы к этому моменту совершили работы, то они охладились до температуры T0. При сгорании пороха 
выделилось тепло 
, что эквивалентно работе 
. Если обозначить через 
- средняя теплоемкость газа при постоянном объеме в интервале температур, то количество тепла в 1-м кг. газе будет 
, внутренняя энергия газа
была бы равна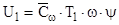 
. Такое количество энергии могло бы перейти в работу, если температура понизилась бы до нуля градусов по Кельвину. В действительности температура газа, совершившего работу понизилась до температуры T<T1 и следовательно содержит в себе внутреннюю энергию
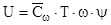. Следовательно 
(9,13) или
= 
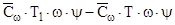(9,14)
Подставив выражение 
получим 
(9,15)
В момент t = tд T=Tд и 
. В связи с тем, что значение "b" очень мало по сравнению с "a" то значение 
мало меняется от температуры и можно принять ее средней для всего процесса. Т.е. уравнение (9,14) примет вид
(9,15)
Принимая отношение 
где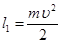 
- энергия поступательного движения снаряда; ki – коэффициент, зависящий от вида работ, и обозначая 
= 
,
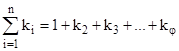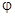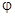- коэффициент, учитывающий все виды работ. Получим
Из термодинамики известно
(9,16)
и 
(9,17)
или k-1= 
= 
;
Если представить 
и 
получим
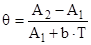
и среднее значение
которому будет соответствовать 
(9,18)
тогда уравнение (9,15) примет вид:
Выражение 
где W – свободный объем.
…. пространства, он равен
где 
- свободный объём каморы к моменту сгорания в ней части заряда .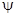
Sl-объём канала ствола, образованный в результате перемещения снаряда.
Окончательно получим уравнение Резаля:
(9.19)
при постоянном объёме,полагая 
, 
, получим уравнение пиростатики 
(9.20),т.е.
значение -среднее значение в диапазоне температур Т1 и Тд, 
.В таблице приведены средние значения в зависимости от степени расширения газа,вычисленное по формуле 
| 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,1 | |
| |||||||
| 0,185 | 0,190 | 0,196 | 0,202 | 0,208 | 0,215 | 0,232 |
9.2 Баллистические коэффициенты.
Уравнение большой энергии при выстреле справедливо не только для первого периода выстрела но и для второго периода,когда порох сгорел,тогда: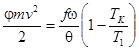 
(9.21)
при Т=0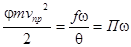 
(9.22),где П –потенциал пороха
-предельная скорость снаряда.
Хотя выражение для П имеет только теоретическое значение,т.к. на практике нельзя получить при выстреле охлаждение газов до абсолютного нуля,тем не менее оно показывает, что можно увеличить работоспособность пороховых газов либо посредством увеличения силы пороха (увеличение удельного объёма и температуры горения)либо уменьшения величины 
.Величина зависит от состава и температуры газов,следовательно, порох с более высокой температурой горения –Т1 будет обладать большим запасом работы (потенциалом) не только за счет силы-f, но и за счет меньшей величины (при неустановившемся течении газа роль существенно возрастает, что будет показано далее).
Предельная скорость снаряда - соответствует использованию всего
закона энергии до конца и КПД равному единице. Хотя на практике этой величины нельзя достигнуть,но они входят множителем в формулы для скорости снаряда 
,как в первом так и во втором периодах выстрела и обычно с увеличением растет растёт и действительная скорость снаряда. Из выражения (9.22) получим:
(9.23)
Таким образом растёт с увеличением потенциала пороха- П, с увеличением относительного веса заряда 
и с уменьшением коэффициента фиктивности - 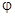.Так как 
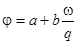,то 
при →∞ 
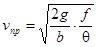
при b=1/3 
; 
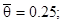
, получим 
Отметим,что 
справедливо при квазиустановившемся течении газа (для не установившегося течения газа значение предельной скорости будет значительно выше).
Для случая,когда Тд 
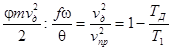
В этом соотношении 
представляет термический коэффициент полезного действия цикло Карно обозначая КПД через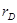 
, получим
(9.24)
Величина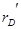 
имеет большое значение в теории баллистического проектирования,т.к. она учитывает всю совокупность работ совершаемых газами в орудии. Наряду с 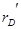используется термический КПД.
(9.25)
где 
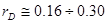
В некоторых руководствах полный запас работы выражают 
где 
-количество тепла определенное по опытам в калориметрической бомбе при сгорании 1 кг пороха и охлаждении газов до температуры 150С.
Величина 
-работа, которую мог бы совершить газ при охлаждении до 00К. Таким образом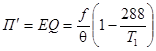 
, т.е. 
процентов 10% при Т1=2700-2800К. Это необходимо учитывать при расчетах.
Характерным параметром выстрела является: коэффициент использования единицы веса заряда - 
, выражающий величину кинетической энергии в момент вылета снаряда из канала ствола или дульную энергию снаряда, приходящуюся на единицу веса заряда:
(9.26)
Этот коэффициент важен с экономической точки зрения (со стороны пороха) и для определенных систем орудий постоянен по величине (для недлинных пушек среднего калибра 
, для стрелкового оружия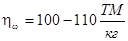 
, а для гаубиц 
. С увеличением начальной скорости снаряда увеличивается значение и большая часть энергии тратится на перемещение заряда, поэтому 
убывает до 90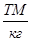 
и ниже. и 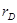связаны соотношением: 
Важной характеристикой орудия является коэффициент полноты индикаторной диаграммы 
на полном пути снаряда по каналу орудия - 
, он обозначается:
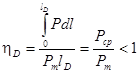или 
(9.27)
где Wд=SlD- рабочий объём канала ствола.
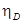можно назвать коэффициентом использования рабочего объёма канала ствола.
Для орудий величина 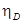колеблется от 0,40 до 0,70. Для характеристики использования всего объёма канала орудия, включая и объём калибра выведем величину: 
; (9.28)
которую можно называть коэффициентом баллистического использования всего канала ствола.Баллистический коэффициент –RD важен с точки зрения сосредоточения в единицу металла побольше энергии,т.е. чтобы труба была более легкой, скорость снаряда была бы большой. В этом одна из особенностей баллистики от электро- и теплотехники.
Действительно пусть канал ствола –цилиндр.Толщина стенок зависит от Рm –максимального давления пороховых газов,т.е.
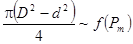,где D и d – наружний и внутренний диаметр ствола 
, тогда 
(9.29)
означает сколько на единицу энергии приходится в единицу веса трубы.
Из уравнений (9.28) R→0 если Wкн→W0
R→0 если Wкн→∞
при lD=0 Wкн=W0 
R=0
при lD=0 Wкн=∞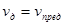 
R=0
Отсюда, видно,что если 
возрастающая функция от Wкн, то R имеет максимумы при некотором значении Wкн.
