Под дифракцией понимается способность волн огибать встречающиеся на пути препятствия, иными словами, отклоняться от прямолинейного распространения. Чтобы наблюдать дифракцию световых волн, необходимы определенные условия: либо размеры препятствий (или отверстий) должны быть очень малыми, либо расстояние от препятствия до наблюдаемой картины должно быть велико. Дифракцию можно наблюдать, например, следующим образом: поставим на пути лучей от точечного источника света преграду с очень малым круглым отверстием, тогда на экране, помещенном за отверстием, увидим систему чередующихся светлых и темных колец.
Чем уже отверстие, тем на больший угол отклоняются лучи за отверстием, тем больше диаметр колец. Если вместо круглого отверстия будет узкая щель, то дифракционная картина будет иметь вид чередующих светлых и темных полос. При использовании белого света дифракционная картина приобретает радужную окраску.
Дифракционные картины нередко наблюдаются в естественных условиях. Так цветные кольца, окружающие источник света, наблюдаемые сквозь туман или через запотевшее оконное стекло, обусловлены дифракцией света на мельчайших водяных каплях.
Явление дифракции света подтверждает его волновую природу и объясняется с помощью принципа Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени (см. Рис.1.20). S – фронт волны – геометрическое место точек, колеблющихся в одинаковой фазе.
Принцип Гюйгенса является чисто геометрическим, он не указывает способа расчета амплитуды волны, огибающей вторичные волны.
Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей об интерференции вторичных волн. Согласно принципу Гюйгенса – Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн.
Рис.1.20
Если источник света находится далеко от наблюдателя, т.е. лучи можно считать параллельными, то говорят о дифракции Фраунгофера. Дифракция в расходящихся лучах, когда волновой фронт имеет форму сферы (например, от близкого точечного источника) называется дифракцией Френеля (Рис.1.20).
Изучим дифракцию Френеля пользуясь принципом Гюйгенса-Френеля, для него найдем амплитуду колебаний в точке Р, возбуждаемых сферической монохроматической волной, распространяющейся в однородной среде от источника S (Рис. 1.21).
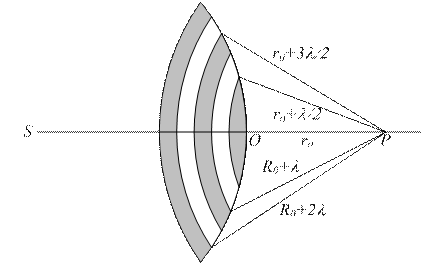
Рис. 1.21
Будем считать, что сферическая волна симметрична относительно направления ее распространения S-P. Разобьем волновую поверхность на ряд кольцевых зон, причем расстояние от каждого соседнего кольца до точки наблюдения Р будет отличаться на λ/2. При этом колебания от соседних зон будут приходить в точку Р в противоположных фазах и будут ослаблять друг друга. Так как расстояние от зон до точки Р по мере увеличения их номера и удаления от центра сферы О растет, то амплитуда колебаний, доходящих от них в точку Р, монотонно убывает, т.е. А1>А2>А3…>Аn-1>Аn>Аn+1.
Так как фазы колебаний от соседних зон противоположны, то результирующая амплитуда колебаний в точке Р:
Ар=А1-А2+А3-А4+…
или
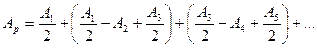
Суммы в скобках можно считать равными нулю.
Тогда 
т.е. действие всей волновой поверхности (Рис.1.21) эквивалентно половине действия первой (центральной) зоны. Центральная зона очень узкая, поэтому можно считать, что свет от нее распространяется прямолинейно. Если на пути волны поставить преграду с отверстием, пропускающим свет только от центральной зоны, то амплитуда Ар в точке Р возрастет в 2 раза, а интенсивность I=А2 увеличится в 4 раза. По мере увеличения диаметра отверстия интенсивность I света в точке Р будет периодически меняться: если отверстие открывает нечетное число зон - наблюдается максимум, если четное - минимум. Пластинка, выборочно пропускающая свет от зон Френеля, получила название зонной пластиной.
Подобным же образом можно объяснить наблюдение максимумов (или минимумов) за круглым непрозрачным препятствием. Если на пути S-P мы перекроем, например, две зоны, то в точке Р амплитуда будет:
Ар=А3-А4+А5-А6+……
По мере увеличения размеров препятствия увеличивается число перекрытых зон и интенсивность в точке Р уменьшается, стремясь к нулю. Можно объяснить, что свет способен огибать лишь малые препятствия.
