Гармонические колебания можно представить с помощью вектора амплитуды А, вращаемого с циклической частотой ω (Рис.1.4). Проекция вектора А на ось х будет меняться со временем по закону (1.3).
Рис. 1.4
Таким образом, проекция вектора на ось х будет совершать гармонические колебания с амплитудой, равной длине вектора А, циклической частотой, равной угловой скорости вращения, и начальной фазой, равной углу φ0, образуемому вектором А с осью х в начальный момент времени t=0.
Рассмотрим сложение колебаний одинакового направления (с одинаковой частотой ω, но отличающиеся начальными фазами и амплитудой).
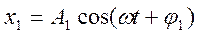
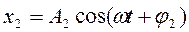
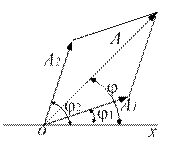
Рис. 1.5
Результирующая амплитуда (рис. 1.5) по правилу векторного сложения:
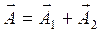
Угол φ для результирующей амплитуды определяется:
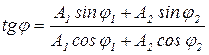
Уравнение результирующего гармонического колебания будет:
.
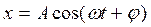Если же частоты складываемых колебаний различны, то результирующее колебание не будет гармоническим.
Особый интерес представляют два гармонических колебания, незначительно отличающиеся по частоте. Тогда при сложении получается колебание с пульсирующей амплитудой. Такие колебания называются биениями.
Рассмотрим сложение взаимно перпендикулярных колебаний.
Пусть материальная точка на пружине участвует сразу в двух колебаниях вдоль осей х и y (Рис.1.6):
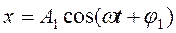
Получим уравнение результирующего колебания, исключая время из этих уравнений:
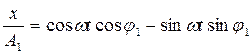(1.18)
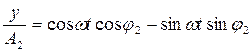(1.19)
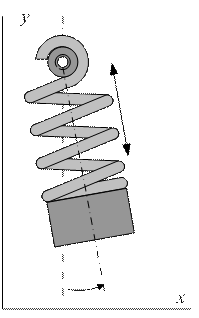
Рис. 1.6
Умножим первое равенство на cos φ2, второе - на cos φ1 и найдем их разность:
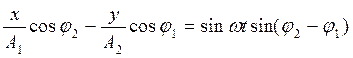. (1.20)
Повторим то же самое только первое равенство, умножим на sin φ2, второе - на sin φ1 и найдем разность:
. (1.21)
Возводя уравнения (1.20) и (1.21) в квадрат и складывая, получим:
.
Это уравнение эллипса.
В частных случаях:
а) при φ2 – φ1=0 получим:
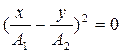или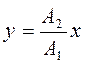 
- уравнение прямой.
б) при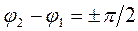 
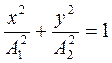- уравнение эллипса, приведенного к осям координат.
Знаки ± указывают только направление вращения материальной точки вдоль траектории – эллипсу (по часовой или против часовой стрелки).
в) при А1=А2 получим:
х2+у2=А2
– уравнение окружности с радиусом А.
И, наконец, если частоты ω взаимно перпендикулярных колебаний различны, то траектории результирующего движения представлены сложными кривыми, называемыми фигурами Лиссажу. Ниже на рисунке 1.7 приведены результаты сложения взаимно перпендикулярных гармонических колебаний одинаковой амплитуды с кратными частотами, отличающимися как 1:2; 1:3; 1:4 и 3:4. Во всех случаях начальные фазы колебаний были равны нулю.
Те же отношения частот при наличии фазового сдвига в начальный момент времени дают несколько иные картины, показанные на Рис. 1.8. Таким образом, вид траекторий чувствителен не только к соотношениям частот, но и значениям фаз колебаний. Это обстоятельство используется при осциллографическом методе определения метрологических характеристик генераторов и настройке радиотехнических устройств.
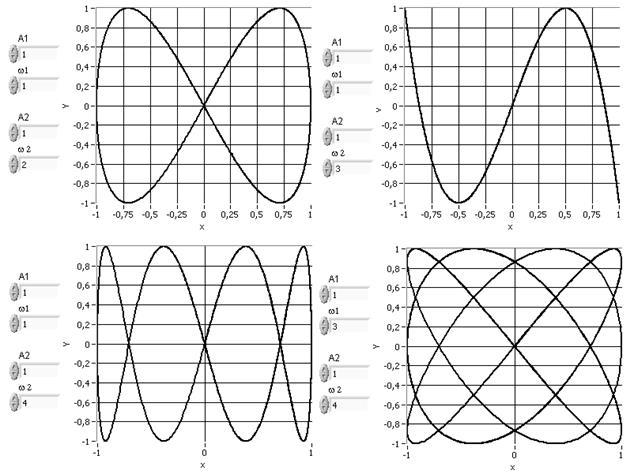
Рис.1.7
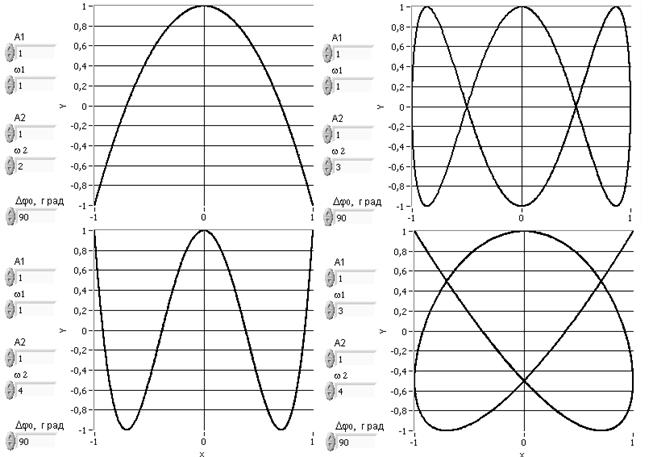
Рис.1.8
1.6. Электрические колебательные системы, колебательный контур.
Колебательный контур (Рис. 1.8) – осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
Рис.1.8
Колебательный контур – простейшая система, в которой могут происходить свободные электромагнитные колебания.
Пусть конденсатор ёмкостью C заряжен до напряжения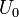 
. Энергия, запасённая в конденсаторе
.
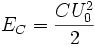При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток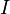 
, что вызовет появление в катушке электродвижущей силы (ЭДС) самоиндукции, направленной на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора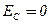 
. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
,
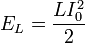где 
– индуктивность катушки,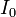 
– максимальное значение тока.
После этого начнётся перезарядка конденсатора, которая будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения 
.
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
Согласно закону Ома для контура, представленного на рис 1.8,
,
где IR -падение напряжения на резисторе R, 
- напряжение на конденсаторе, 
- ЭДС самоиндукции при изменяющемся токе. Тогда
.
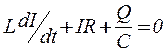Разделив на L и подставив 
и 
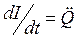, получим уравнение затухающих колебаний типа (1.14)
(1.22)
Если внешние ЭДС отключены и R мало, то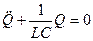 
- уравнение свободных гармонических колебаний типа (1.6) с собственной частотой 
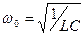и периодом, определяемым формулой Томсона:
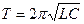
При этом колебания заряда 
; тока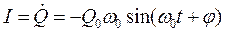 
; напряжения 
.
При R≠0 колебания будут затухающими, и описываются уравнением типа (1.14). Обозначая через 
и 
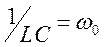, получим для контура дифференциальное уравнение второго порядка:
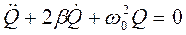, (1.23)
решением его будет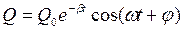 
, где частота 
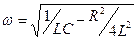меньше собственной 
.
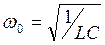Добротность контура при этом:
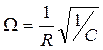
Вынужденные колебания возникают в системе под действием внешней периодически меняющейся силы. Рассмотрим это на примере электрического колебательного контура, в котором роль вынуждающей силы будет играть внешняя ЭДС периодически изменяющаяся по гармоническому закону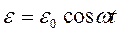 
. Тогда уравнение (1.23) запишется:
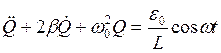(1.24)
Можно показать, что общее решение неоднородного уравнения (1.24) позволяет для установившегося режима колебаний получить для тока в контуре:
,
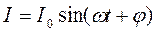где
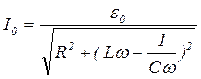и 
.
При постоянном R амплитуда тока I0 будет максимальна при 
. Тогда 
и ω=ω0. Наблюдается явление резонанса. Зависимости амплитуды вынужденных колебаний I0 от частоты ω для разных значений сопротивлений показаны на Рис.1.9.
Рис. 1.9.
В расчётах приняты значения L= 100 нГн, С= 0,1мкФ, сопротивления заданы в Ом.
