Выборочных показателей

Если генеральная совокупность велика, ее приравни­вают к бесконечности. В этом случае ошибку выбороч­ной средней арифметической (X) вычисляют по фор­муле:

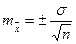
где m_x —ошибка средней арифметической (x); σ —среднее квадра-тическое отклонение; n — объем выборки.

Согласно этой формуле, ошибка средней арифме­тической величины зависит от σ и n (чем меньше разно­образие признака, тем меньше ошибка). При полной однородности совокупности по изучаемому признаку (σ=0) средняя ошибка становится равной нулю, т. е. X выборки становится равной X генеральной совокупно­сти. Величина средней ошибки находится в обратной зависимости от п. Чем больше вариант вошло в выбор­ку, тем меньше ошибка выборочной X.

В малочисленных выборках она вычисляется по сле­дующей формуле:

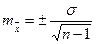
В выборке из 100 коров определен средний суточный удой X =21,26 кг, а σ=±3,68. Ошибка средней арифме­тической в данном случае составит

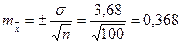кг

Это означает, что средняя ошибка на 100 голов состав­ляет 0,368 кг. Следовательно, среднесуточные удои изу­чаемой выборки характеризуются Х±m=21,26±0,368.

Доверительные границы для средней арифметиче­ской гнеральной совокупности X находятся в пределах: X=X~±t х m (27). Верхняя граница 21,26+1,17=22,43; нижняя — 21,26—1,17=20,9.

Ошибки других выборочных показателей вычисляют по следующим формулам:

среднего квадратичного отклонения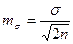

коэффициента вариации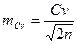

коэффициента корреляции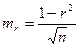

коэффициента регрессии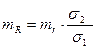

Величину выборочного показателя записывают с ве­личиной его ошибки со знаком «±х» Х±т, σ±тσ, Cv±m_cv, r±m_r и т. д. Достоверность выборочных пока­зателей (± t) определяется отношением выборочного показателя к его средней ошибке по формулам:

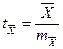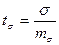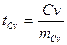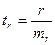; ; ; (32-35)