Во многих исследованиях возникает необходимость сравнить средние арифметические двух групп животных (например, среднюю живую массу животных опытной и контрольной групп или
среднюю продуктивность дочерей двух производителей и т, д.). Средние двух сравниваемых групп всегда в некоторой мере отличаются друг от друга. Поэтому необходимо установить, досто-. верна ли разность между средними. 
При решении задач такого рода определяют разность (d) ме-жду двумя средними (Х1 и Х2) путем вычитания: d=X1 — X2. Среднюю ошибку разности (тd) вычисл яют по формуле:
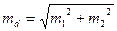(36)
Достоверность разности (td) определяется по формуле:
или 
td= 
(37
В таблице 11 приведены три стандартные величины и соответствующие им вероятности. Так, например, при t = 2,57 вероятность того, что разность достоверна, составляет 0,99 (т. е. 99%), а при t =3,2 вероятность достигает 0,999 (99,9%). Если же величина td меньше 1,96, то разность между средними сравниваемых групп не может быть признана достоверной.
При сравнении малых выборок вычисление тd. по формуле (28) можно производить только в том случае, если объемы выборок (п) не отличаются резко друг от друга, в других случаях пользуются таблицей Стъюдента.
Пример. Сравнивается молочная продуктивность первотелок бестужевской и холмогорской пород (большие выборки). В одинаковых условиях кормления и содержания получены следующие показатели удоя за 1-ю лактацию: по красному белорусскому скоту: X1±m1 =3600±30кг; по белорусской черно-пестрой породе X2±m2 =4200±40 кг.
Установить достоверность разности между удоями в этих группах. Вычисляя td по формуле (37) (а, б), получаем:
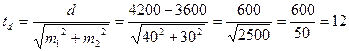
Критерий достоверности разницы (td= 12 ) значительно превышает величины, приведенные в таблице 11. Поэтому можно с вероятностью, превышающей 99,9%, утверждать, что коровы белорусской черно-пестрой породы более обильномолочны по сравнению с коровами красного белорусского скота.
Второй пример. Изучается эффективность влияния микроэлементов при откорме бычков. С этой целью сформированы две группы животных (опытная и контрольная) с одинаковой средней живой массой, по 14 голов в каждой. Обе группы откармливаются на одинаковых рационах, но животные опытной группы получают микроэлементы.
После окончания опыта и обработки первичных данных получены следующие результаты: средняя живая масса (X1) в опытной группе 300 кг, в контрольной (X2) — 260 кг. Средние ошибки для опытной и контрольной групп соответственно равны: т1 = 9 кг, т2 =6 кг. Достоверно ли различие в массе животных опытной и контрольной групп?
Несмотря на то что сравниваются малые выборки, ошибку разности можно определить по формуле (28), так как в обеих группах одинаковое число животных.
Следовательно,
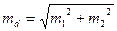=√92+62=10,8
= 
=3,7
Значение вероятности, соответствующее найденному td, определяем по таблицам Стьюдента (приложение 1). Для этого находим число степеней свободы (v). В данном примере сравнение двух выборок будет равно v= n1+ n2 —2=14+14—2=26. Находим в таблице строку v = 26. Из пяти стандартных значений t, находящихся в этой строке, находим число, равное или большее установленного в опыте (td = 3,7). Такое число находится в последнем столбце. Верхняя строка этого столбца показывает искомую вероятность Р= 0,999. Следовательно, разность d =40 кг можно считать высокодостоверной.
При Р = 0,999 этот результат следует подчеркнуть тремя черточками (d =40); при Р, равном 0,99, — двумя, а при Р, равном 0,95, — одной черточкой.
Занятие 5
КРИТЕРИЙ ХИ-КВАДРАТ (χ2)
Цель занятий. Освоение метода хи-квадрат, использование его при решении генетико-селекционных, ветеринарных и других задач.
Методические указания. Критерий хи-квадрат используется для проверки гипотез путем сравнения фактического распределения с теоретическим.
Использование ошибок выборочных показателей и сравнение двух вариационных рядов основаны на нулевой гипотезе (Н 0), которая предполагает, что между сравниваемыми выборками нет достоверных различий. Нулевая гипотеза опровергается или остается в силе. Критерием оценки этих суждений является уровень достоверности — Р.
Вычисление критерия соответствия хи-квадрат также основано на принципах нулевой гипотезы. Критерий Хи-квадрат используют при сравнении частот двух эмпирических рядов или сравнении эмпирических рядов с теоретическими, при гибридологическом анализе, при проверке различных гипотез, при оценке эффективности применения лекарственных средств, закономерности распределения частот в популяциях и др. Критерий хи-квадрат — показатель приближенный. Он применим для выборок численностью 20 особей и более. Его нельзя использовать, когда частоты выражаются в относительных величинах. Критерий хи-квадрат вычисляется по формулам:
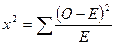(38)
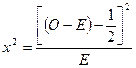(39)
где О — наблюдаемое число особей; Е — теоретически ожидаемое число особей; член1/2— поправка Иетса.
Если п и ожидаемые величины велики, то можно пользоваться формулой (38) без поправки.
Применение хи-квадрата при изучении наследования качественных признаков. При спаривании особей, отличающихся друг от друга одной парой признаков, в потомстве происходит расщепление в отношениях 1:1 или 3:1; при различиях родителей по двум парам признаков — в отношениях 9:3 или 3:1 и т. д. Эти отношения берутся в качестве нулевой гипотезы, после чего проверяется соответствие наблюдаемого в опыте расщепления с данными нулевой гипотезы. Результаты позволяют либо принять ее, признав пригодной для объяснения результатов опыта, либо отвергнуть. Например, во втором поколении моногибридного скрещивания, состоящем из 8024 особей, получено 6023 особи с доминантным признаком и 2001 с рецессивным. Теоретически ожидается расщепление 3:1.
Наблюдаемое в опыте соотношение особей с доминантными и рецессивными признаками (6023:2001) неточно отвечает ожидаемому (3:1). Однако если это зависит от случайных причин, то нет основания считать,что наблюдаемые данные не согласуются с нулевой гипотезой. При вычислении критерия хи-квадрат следует расположить данные, как в таблице 12. Соотношение ожидаемых частот 3:1 составит для особей с доминантным признаком 3/4 х 8024 = 6018, для особей с рецессивным признаком — '/4 х 8024=2006.
Полученная 
, представляет собой величину хи-квадрат. В данном примере χ2 =0,0165.
