Расчет коэффициентов корреляции между суточным удоем и живой массой коров

у х

12-13,9

14 – 15,0

16 -17,0

18 – 19,9

20 -21,9

22 -23,9

24 -25,9

26 -27,9

28 -29,9

30 – 31,9

f

ay

fay

Fa2y

550-569 1 1 +5 +5 25

530-549 2 7 +4 +28 112

510-529 8 2 10 +3 +30 90

490-509 1 1 3 5 +2 +10 20

470-489 4 15 19 +1 +19 19

450-469 20 16 36 0 0 0

430-449 5 5 -1 - 5 5

410-429 2 7 1 10 - 2 - 20 40

390-409 4 4 - 3 - 12 36

370 -389 1 1 1 3 - 4 - 12 48

f 1 10 5 4 43 17 10 8 2 1 100

a_x - 4 - 3 -2 -1 0 +1 +2 +3 +4 +5

fa_x -4 -30 -10 -4 0 +17 +20 +24 +8 +5

fa²_x 16 90 20 4 0 17 40 72 32 25

 

Затем выполняют обычные вычисления по каждому вариационному ряду порознь тем же способом, как при вычислении сигмы. f_x — частоты вариационного ряда по удоям; f_y — частоты вариационного ряда по живой мас­се; ах и ау — отклонения от условного среднего класса. Суммируем с учетом знака значения fxax по удою и fyаy по живой массе: ∑ f_xax =+74-48 = +26; ∑f_yay = =+92—49=43.

Суммируем значения fa² для каждого из рядов ∑f_xa_x = 316, ∑ f_y a² _y = 395. По этим данным вычисляют для каждого ряда значения β, по формуле (16) и S по формуле (17).

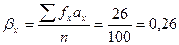
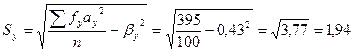
Чтобы вычислить коэффициент корреляции (по фор­муле 15), кроме β и S, необходимо знать ∑fa_xa_y, где f — число животных в одной клетке решетки; а_х — отклонение от условного среднего класса по молочности; а_у — отклонение от условного среднего класса по живой массе. Вычисления производят отдельно по каждому из че-тырех квадрантов. Отклонения а_у умножают на частоту f в ячейке корреляционной решетки и на отклонение а_х. Если в клетках частоты отсутствуют, вычислений не производят. После умножения результаты суммируют и получают ∑fa_xa_y по каждому квадранту.

/ квадрант II квадрант III квадрант

(-4)1(-4) =+16 (+1)4(-1)=-4 (+5) 1 (+5) = +25

(_4) 1 (-3) = +12 (+2) 1 (-3) = -6 (+4) 5 (+3) = +60

(-3) 4 (-3) = +36 (+4) 2 (-3) = -24 (+3) 2 (+4) = +24

(-2) 2 (-3) = +12 ∑fa_xa_y= -34 (+3) 8 (+2) = +48

<-1)5(-2)=+10 (+2) 1 (+1) = +2

∑fa_xa_y=+86 (+2)3(+3) ₌ +18

∑fa_xa_y =+177 |

IV квадрант

(-4)1 (+2) = —8 ∑fa_xa_y =177 + 86 — 34—12 =
(-2) 1 (+2) = -- 4 =+263-46 =+217

∑fa_xa_y =-12

Подставляем значения ∑fa_xa_y,, β_х, β_у,, S_х, S_y в форму­лу (15).

Связь при r = 0,5 и выше считается значительной, при r =0,3—0,49 — средней, r <0,3 — малой.

Вычисленное значение коэффициента корреляции по­казывает, что между суточным удоем и живой массой коров существует значительная положительная связь. При отборе более крупных коров удой в стаде будет по­вышаться.

Вычисление коэффициента корреля­ции для альтернативных признаков (r_a). Корреляция между альтернативными признаками из­меряется тетрахорическим показателем связи.

При изучении у каждой особи двух альтернативных признаков группа разбивается на четыре части: Р₁ —особи, имеющие оба признака (++); Р₂— особи, име­ющие первый признак, но не имеющие второго признака (+—); Р₃ — особи, не имеющие первого признака, ноимеющие второй признак (—+ ), Р₄ —особи, не имею­ -
щие обоих признаков (-- --).

Тетрахорический показатель связи вычисляется; по формуле:

(18)

Пример. При изучении влияния отселекционированности на резистентность цыплят к пуллорозу оказа­лось, что после заражения живой культурой из 220 цыплят выжило 115, пало-105, а в отселекционированной группе выжило 560, пало 58.

Определить тетрахорический показатель связи между резистентностью цыплят к пуллорозу и степенью отселекционированности стада по этому показателю.

Для вычисления тетрахорического показателя свя­зи необходимо показатели разнести в четырехпольную корреляционную решетку (табл. 9).