Цепи Маркова с непрерывным временем задаются матрицей инфинитезимальных характеристик 
, элементы которой определяются следующим образом:
,
, 
.
Величина 
имеет смысл 
интенсивности перехода цепи Маркова из состояния 
в состояние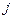 
, а величины 
– смысл интенсивности выхода из состояния .
Кроме того, они обладают свойством 
.
Из определения инфинитезимальных характеристик можно определить вероятности перехода за время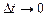 
:
,
.
Матрица инфинитезимальных характеристик позволяет найти вероятности 
для любых 
. Эти вероятности удовлетворяют прямой и обратной системам дифференциальных уравнений Колмогорова.
Для неоднородных цепей Маркова:
обратная система дифференциальных уравнений Колмогорова имеет вид:
,
где 
– краевые условия, заданные на правой границе 
области изменения переменной 
.
прямая система дифференциальных уравнений Колмогорова имеет вид:
,
где 
– краевые условия, заданные на левой границе 
области изменения переменной 
.
Для однородных цепей Маркова эти системы записываются следующим образом:
