Пусть для цепи Маркова единственный замкнутый класс 
. Обозначим 
– среднее значение времени перехода цепи Маркова из несущественного состояния 
в замкнутый класс . Учитывая, что если из состояния можно сразу попасть в класс 
, то время перехода равно единице, а если этот переход выполняется в несущественное состояние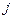 
, тогда суммарное время перехода составляет 
, где первое слагаемое, равное единице, определяет первый шаг, а второе: 
– среднее значение времени перехода из состояния 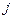в класс .
В силу формулы полной вероятности для условных математических ожиданий, можно записать систему линейных неоднородных уравнений для определения :
.
Если цепь Маркова содержит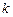 
замкнутых классов, то для нахождения среднего времени перехода из несущественного состояния в 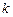-ый замкнутый класс , необходимо учитывать вероятность перехода в этот замкнутый класс, то есть находить условное время перехода. 
, где 
– событие, состоящее в том, что из -го состояния мы перешли в 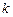-ый замкнутый класс. Это время перехода определяется равенством:
,
где 
определяется аналогично для цепи Маркова с единственным замкнутым классом состояний.
ПРИМЕР. Найдите вероятность и условное среднее время перехода из несущественного состояния в замкнутый класс для цепи Маркова, заданных матрицей переходов за один шаг систем
.
Граф состояний для заданной цепи Маркова имеет вид
Очевидно, что у рассматриваемой цепи состояние 3 – несущественное и есть два неразложимых класса 
, 
.
Следовательно, рассмотри две гипотезы:
- произошел переход в замкнутый 
;
- произошел переход в замкнутый .
Тогда условное среднее время перехода из несущественного состояния в замкнутые классы и определяется по формулам:
,
,
где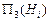 
– вероятность события 
, то есть вероятность перехода из несущественного состояния 3 в -ый замкнутый класс.
Вероятности перехода из несущественного состояния 3 в замкнутые классы и 
определяем по формулам
,
.
Откуда получаем: 
, 
.
Для 
и 
имеем систему уравнений:
, 
;
, 
.
Тогда условное среднее время перехода из несущественного состояния в замкнутые классы и составляет:
,
.
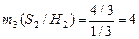