Для цепи Маркова 
определим
–
вероятность первого возвращения в состояние 
на 
-м шаге, тогда 
– вероятность того, что система, выйдя из состояния , хотя бы один раз вернется в него.
Определение. Состояние 
называется возвратным, если 
, и невозвратным, если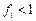 
.
Все состояния конечного эргодического класса возвратны. Невозвратные состояния возможны только при бесконечном числе состояний.
Если состояние 
возвратно и 
, то состояние 
также возвратно.
Если состояние 
возвратно, то есть , то набор вероятностей 
образует распределение вероятностей времени возврата.
Поскольку отыскание функций довольно сложно, то для определения возвратности состояний полезен следующий критерий.
Критерий возвратности состояний. Состояние возвратно тогда и только тогда, когда 
.
Каждое возвратное состояние можно в свою очередь отнести к одному из двух типов в зависимости от величины среднего значении времени возвращения (от его конечности или бесконечности). Величина 
по определению математического ожидания равна среднему значению числа шагов, за которые цепь Маркова возвращается в состояние . Величина 
, очевидно, характеризует интенсивность возвращения в состояние .
Определение. Возвратное состояние называется положительным, если 
, и нулевым, если 
.
Пример. Рассмотрим одномерное случайное блуждание частицы по целочисленным точкам действительной прямой. За каждый переход частица перемещается на единицу вправо с вероятностью 
и на единицу влево с вероятностью 
, причем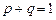 
.
Следовательно, используя формулу Бернулли, получаем
, 
, 
Воспользовавшись формулой Стирлинга 
получаем
.
Так как 
, причем равенство имеет место только тогда, когда 
, то 
. Поэтому ряд 
расходится тогда и только тогда, когда , и в данном случае все состояния являются возвратными.
При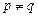 
, когда 
и 
, все состояния являются невозвратными. Очевидно, что если 
, то частица, отправляясь из состояния , будет смещаться вправо к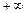 
, а если 
, то влево к 
.
