Классифицировать состояния цепи Маркова, заданной матрицей вероятностей переходов за один шаг.
Граф переходов для данной цепи Маркова имеет вид
Рис. 2.
Очевидно, что у рассматриваемой цепи состояния 1,4,2 – несущественные, 3,5,6,7 –существенные, кроме того, есть два неразложимых класса 
, 
. Следовательно, канонический вид матрицы вероятностей переходов следующий:
Рассмотрим теперь неразложимый класс, изображенный на рис.3
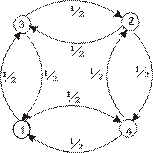
Рис. 3.
Заметим, что здесь возвращение в каждое состояние возможно лишь за четное число шагов, переход в соседнее состояние – за нечетное число шагов, а матрица вероятностей переходов имеет блочную структуру:
Отсюда видно, что класс 
разбивается на два подкласса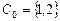 
и 
, обладающих следующим свойством цикличности: за один шаг цепь Маркова из 
непременно переходит в 
, а из – в , но за два шага возвращается в исходный класс. Этот пример показывает возможность разбиения неразложимых классов на циклические подклассы.
Определение. Будем говорить, что состояние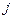 
замкнутого класса имеет период 
, если есть наибольший общий делитель чисел 
таких, что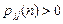 
.
Очевидно, что для предыдущего примера (рис3) 
, для всех 
.
Определение. Если 
, (
), то состояние 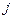(класс 
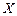) называется апериодическим (эргодическим).
Возвращаясь к циклическим подклассам, можно сделать вывод о том, что если в начальный момент времени система находится в состоянии подкласса , то в момент времени 
, она будет находиться в подклассе 
. Следовательно, с каждым из подклассов 
можно связать новую марковскую цепь с матрицей вероятностей переходов 
, которая будет неразложимой и апериодической. Поэтому в дальнейшем при рассмотрении предельных свойств вероятностей 
при 
, можно ограничиться только эргодическими классами.
