ЛИНЕЙНАЯ АЛГЕБРА
Изд-во АлтГТУ
Барнаул 2010
УДК 51(075.8)
Кобзарь Л.М. Линейная алгебра/ Л.М. Кобзарь, Е.В. Мартынова, В.М. Кайгородова; Алт. гос. техн. ун-т им. И.И.Ползунова. - Барнаул: Изд-во АлтГТУ, 2010. – 169с.
В учебно-методическом пособии приводятся лекции и решение типичных задач по линейной алгебре, и в помощь преподавателю даны 30 вариантов тестовых заданий для самостоятельной работы студентов и организации практических занятий, охватывающие весь курс линейной алгебры. Содержание задач соответствует программе по математике для всех специальностей. В помощь студентам разобраны наиболее типичные задачи и методы их решения, приведены необходимые формулы.
Пособие предназначено для студентов вузов, может быть полезно преподавателям для организации практических занятий и контроля знаний студентов по данной теме.
Рассмотрены и одобрены на заседании кафедры высшей математики и математического моделирования.
Протокол № 6 от 12 марта 2010 г.
Рецензент Лев Г.Ш., кандидат физико – математических наук, доцент (кафедра высшей математики и математического моделирования АГТУ)
Определители 2-го и 3-го порядков, их вычисление и свойства
Определение 1: Прямоугольная таблица чисел вида 
называется матрицей n-го порядка, где числа aij – элементы матрицы, причем i – номер строки, j - номер столбца, i,j 
N(натуральных чисел).
Элементы, стоящие на диагонали, идущей из левого верхнего угла, образуют главную диагональ.
Элементы, стоящие на диагонали, идущей из правого верхнего угла, образуют побочную диагональ.
Пример: Для элемента а23 – цифра 2 - вторая строка и цифра 3 - третий столбец (i, j - это индексы элемента)
Каждой матрице можно поставить в соответствие определенное число.
Определение 2: Определителем (детерминантом) второго порядка называется число, обозначаемое символом ∆ и записываемое в виде
(1)
Числа 
называются элементами определителя. Далее все как у матрицы.
Символика: ∆, 
, detA - обозначение определителя на письме.
Определение 3: Определителем 3-го порядка называется число равное
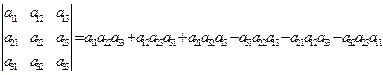(2)
Схематическое изображение вычисления определителя третьего порядка
(метод вычисления по правилу треугольников):
+ 
-
Определение 4: Минором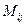 
элемента 
какого-либо определителя называется определитель, полученный из данного, вычеркиванием той строки и того столбца на пересечении которых находится данный элемент.
Пример 1: Найти 
элемента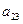 
, если 
Решение:
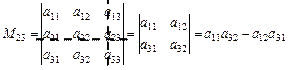
Определение 5: Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком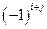 
, т. е. 
(3)
Пример 2: Найти 
элемента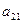 
, если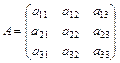 
Решение:
