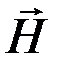Все вещества в магнитном поле способны намагничиваться, т.е. создавать собственное магнитное поле. Такие вещества называются магнетиками. Магнитное поле магнетиков характеризуется вектором намагниченности 
, который равен магнитному моменту единицы объема вещества:
, (1)
где 
– магнитные моменты атомов или молекул, находящихся в пределах малого объема 
. Величина представляет в свою очередь векторную сумму орбитальных и спиновых магнитных моментов электронов, а также магнитных моментов ядер, входящих в состав атомов.
Магнитное поле в магнетике складывается из двух полей: внешнего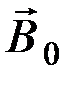 
и внутреннего 
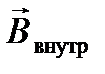, создаваемого намагниченным веществом:
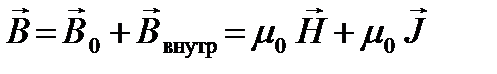, (2)
где 
– напряженность внешнего магнитного поля;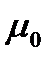 
– магнитная постоянная (4π · 10-7 Гн/м).
Намагниченность связана с напряженностью магнитного поля соотношением
æ 
, (3)
где æ – безразмерная величина, называемая магнитной восприимчивостью вещества. Учитывая (2), индукцию магнитного поля в магнетике можно представить
= 
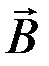æ) 
(4)
или
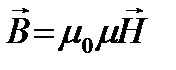(5)
Величина μ, равная
μ = 1 + æ (6)
называется магнитной проницаемостью. Она показывает во сколько раз индукция магнитного поля в магнетике отличается от индукции внешнего поля в вакууме.
По значению магнитной проницаемости μ все вещества делятся на три группы: диамагнетики (μ < 1), парамагнетики (μ > 1) и ферромагнетики (μ >> 1). Особенностью ферромагнетиков является то, что μ не является константой, а зависит от напряженности внешнего поля, т.е. μ = μ (Н).
Диа – и парамагнетики
Диамагнетиками являются вещества, атомы которых, находясь вне магнитного поля, имеют полный магнитный момент 
равный нулю. Только внешнее магнитное поле индуцирует магнитный момент атомов диамагнетика. В результате в нем возникает собственное поле
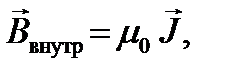(7)
направленное, согласно правилу Ленца, против порождающего его внешнего поля (рис. 1). Все вещества в целом приобретают магнитный момент, направленный противоположно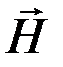 
, поэтому диамагнетик выталкивается из магнитного поля.
| |||||||
| Рис. 1. Возникновение собственного магнитного поля в диамагнетиках (а) и парамагнетиках (б) |
Атомы парамагнетиков обладают магнитным моментом даже в отсутствии внешнего магнитного поля (орбитальные и спиновые магнитные моменты электронов не скомпенсированы). Однако, вследствие хаотического расположения атомов, вещество в целом не обладает магнитным моментом. В этом случае внешнее магнитное поле не только порождает индукционный момент, но и ориентирует магнитные моменты атомов, устанавливая их преимущественно по направлению поля (рис. 1б). Возникающий при этом положительный (т.е. направленный вдоль поля ) магнитный момент значительно больше, чем отрицательный индукционный. В итоге собственное магнитное поле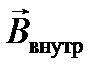 
совпадает по направлению с внешним, и следовательно, парамагнетик втягивается в магнитное поле. Следует отметить, что тепловое хаотическое движение атомов и молекул препятствует строгой ориентации магнитных моментов вдоль поля, поэтому намагниченность парамагнетиков зависит от температуры:
æ =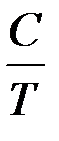 
. (8)
Приведенное соотношение (8) носит название закона Кюри (открыт П. Кюри в 1896 г.). Коэффициент пропорциональности С зависит от рода вещества и находится в пределах 10-5 – 10-6 К.
Все диа – и парамагнетики являются слабо намагничивающимися веществами. Так для диамагнетиков величина магнитной восприимчивости æ ~ 10-6, а для парамагнетиков – æ ~ 10-4. К диамагнетикам относятся многие металлы (Bi, Ag, Au, Cu), парамагнетиками являются редкоземельные элементы (Pt, Al и т.д.)
Ферромагнетики
Свойства ферромагнитных веществ существенно отличаются от рассмотренных выше свойств диа – и парамагнетиков:
1) магнитная проницаемость μ достигает больших значений порядка 102 – 106;
2) намагниченность ферромагнетиков J имеет нелинейную зависимость от H;
| B |
| H |
| Рис. 2. Зависимость индукции магнитного поля от Н от напряженности для различных магнетиков. 1 – ферромагнетики; 2 – парамагнетики; 3 – диамагнетики |
4) способность сохранять намагниченность даже в отсутствие внешнего магнитного поля.
К ферромагнетикам принадлежат железо (наиболее распространенный представитель – отсюда и общее название), никель, кобальт, гадолиний, их сплавы и соединения марганца и хрома с неферромагнитными материалами (MnAlCu, CrFe и др.)
Свойства ферромагнетиков заключаются в особенностях их кристаллической структуры. Ферромагнетик обладает отдельными микроскопическими (линейные размеры ~ 10-6 ÷ 10-4 м) областями (доменами), которые намагничены до насыщения даже в отсутствие внешнего поля. Однако магнитные моменты всех этих доменов ориентированы хаотически, поэтому суммарный магнитный момент макроскопического объема равен нулю.
|
|
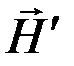
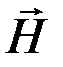
Н = 0 Н ≠ 0 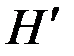 > H
(а) (б) (в)
|
| Рис. 3. Изменение доменной структуры ферромагнетика при намагничивании: а – внешнее поле отсутствует; б – процесс смещения; в – процесс вращения магнитных моментов |
При внесении ферромагнетика во внешнее магнитное поле ориентируются магнитные моменты не отдельных атомов (как в случае парамагнетиков), а целых областей – доменов. Процесс намагничивания делится на три стадии. В начальный момент происходит смещение границ доменов (рис. 3), при этом увеличиваются размеры тех из них, магнитные моменты которых совпадают с направлением внешнего поля. Если на этой стадии внешнее поле выключить, то ферромагнетик вернется в исходное состояние. Таким образом, процесс намагничивания на первой стадии является обратимым.
Процесс смещения границы доменов продолжается по мере увеличения внешнего магнитного поля. Наступает вторая стадия намагничивания. Особенностью этой стадии является необратимость намагничивания, т.е. размеры доменов не возвращаются в исходное состояние, даже при выключении внешнего поля.
Третья стадия наступает при больших значениях напряженности внешнего поля. В этом случае осуществляется процесс вращения магнитных моментов доменов вдоль вектора Н. Завершением этой стадии является насыщение намагниченности, которая наступает при одинаковой ориентации магнитных моментов всех без исключения доменов.
| Рис. 4. Основная кривая намагничивания ферромагнетика. I – процессы обратимого смещения границ; II – процессы необратимого смещения границ; III – процессы вращения |
| J J нас |
| H |
| (III) (II) (I) |
Магнитная проницаемость μ так же является нелинейной функцией от Н, что является следствием зависимости J (H). Действительно из выражения (2) следует:
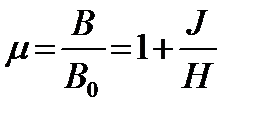. (9)
Когда намагниченность достигает насыщения J нас, а напряженность растет, значение μ стремится к единице. График зависимости μ (H) показан на рис. 5.
Магнитным гистерезисом называется явление запаздывания изменения магнитной индукции В в ферромагнетике по отношению к изменению напряженности Н внешнего поля. В этом запаздывании проявляется зависимость намагниченности от предшествующего его состояния. Петлей гистерезиса (рис. 6) называется кривая изменения магнитной индукции ферромагнетика, помещенного во внешнее магнитное поле, изменяющееся от + Н до – Н и обратно.
При изменении Н от нуля в сторону положительных значений индукция В возрастает, причем кривая сменяется прямолинейным участком после достижения насыщения (см. рис. 2). При уменьшении Н до 0 магнитная индукция запаздывает в уменьшении и при Н = 0 оказывается равной В ост (остаточное намагничивание). Для полного размагничивания образца нужно приложить магнитное поле противоположного направления Н к, называемое коэрцитивной силой (задерживающей напряженностью).
Перемагничивание образца сопровождается потерями энергии магнитного поля, которая затрачивается на переориентировку доменов. Объемная плотность энергии магнитного поля определяется соотношением
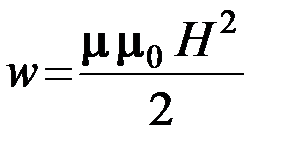. (10)
Изменение энергии при небольшом намагничивании будет:
. (11)
Таким образом, работа магнитного поля за цикл перемагничивания единицы объема ферромагнетика будет равна:
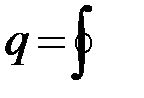d w =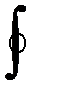 
H dB, (12)
т.е. пропорциональна площади петли гистерезиса. Ясно, что потери внешнего магнитного поля переходят во внутреннюю энергию образца и, в конечном счете, приводят к его нагреванию.
По величинам Н к и q ферромагнетики подразделяются на мягкие (Н к < 100 А/м, малая площадь q) и жесткие (Н к > 100 А/м, площадь q большая). Магнитожесткие материалы используются для создания постоянных магнитов, а магнитомягкие применяются при изготовлении сердечников трансформаторов.
Поскольку разница в энергиях между намагниченным и ненамагниченным состояниями составляет лишь несколько десятых электронвольт, то повышение температуры образца (энергия теплового движения ~ k T) может уничтожить намагничивание доменов. При температуре, называемой точкой Кюри, намагниченность доменов исчезает, и ферромагнетик превращается в парамагнетик. Температура Кюри для различных веществ имеет строго определенные значения. Например, для железа 770°C, кобальта 1127°C, никеля 358°C, гадолиния 16°C.
Теория ферромагнетизма была создана Я.И.Френкелем и В. Гейзенбергом в 1928 г. Из опытов по изучению магнитомеханических явлений следует, что ответственным за магнитные свойства ферромагнетиков являются собственные (спиновые) магнитные моменты электронов. При определенных условиях в кристаллах могут возникать силы, которые заставляют магнитные моменты электронов выстраиваться параллельно друг другу. В результате возникают области спонтанного (самопроизвольного) намагничивания, т.е. домены.
Порядок выполнения работы
Для нахождения зависимости магнитной индукции В внутри ферромагнетика от напряженности магнитного поля Н с помощью электронного осциллографа достаточно подать на одну пару его отклоняющих пластин напряжение, пропорциональное Н, а на другую – пропорциональное В. Это можно осуществить, используя ферромагнитный сердечник с двумя обмотками: первичной (намагничивающей) и вторичной (измерительной) (рис. 7).
Получить напряжение, пропорциональное напряжению, легко. Для этого в цепь первичной обмотки следует включить резистор и с него подать напряжение на вход Х. Получить подобным образом напряжение, пропорциональное В, невозможно, так как ЭДС во вторичной обмотке пропорциональна не самой индукции В, а ее производной по времени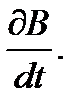 
Поэтому, прежде чем подать напряжение со вторичной обмотки на вход Y, его нужно проинтегрировать с помощью так называемой цепочки RC при правильном подборе ее параметров.
Отклонение луча осциллографа по оси Х будет, таким образом, пропорционально Н, а по оси Y – пропорционально В, и, следовательно, на экране получится график искомой зависимости В от Н при периодическом изменении Н (первичная обмотка питается переменным током), то есть петля гистерезиса, характеризующая исследуемый ферромагнетик.
В работе используется, схема которой приведена на рис. 7. На этом рисунке АТ – автотрансформатор, Тр - понижающий трансформатор, Л – сердечник линейного трансформатора из ферромагнетика с двумя обмотками: намагничивающей N1 и измерительной N2, реостат R1, mA – миллиамперметр, R2 – магазин сопротивлений, С – конденсатор, mV – ламповый милливольтметр, ЭО – электронный осциллограф.
Изменяя величину напряжения на автотрансформаторе (АТ), наблюдать соответствующее изменение формы петли гистерезиса.
Установить на экране осциллографа петлю гистерезиса, зарисовать ее. Записать параметры элементов схемы, данные в приложении. Измерить и записать величины отрезков ОА, ОВ, ОД наблюдаемой петли (рис. 8а).
Отрезок ОА несет информацию о коэрцитивной силе Нк образца:
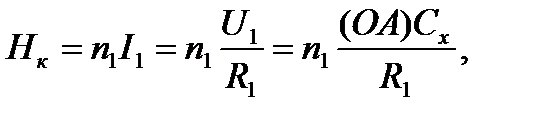(13)
где n1 – число витков на единицу длины обмотки N1; I1 и U1 – соответственно ток в обмотке N1 и напряжение, действующее на резисторе R1, когда магнитная индукция образца обращается в нуль (точка А на петле гистерезиса), Сх – чувствительность осциллографа по каналу Х.
Отрезок ОС несет информацию об остаточной индукции Вост образца:
(14)
Отрезок ОД несет информацию об индукции насыщения Внас образца:
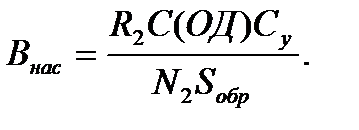(15)
Отрезок ОВ несет информацию о величине магнитного поля, в котором измерена индукция насыщения:
(16)
Вычислите величины Нк, B ост , В нас, Н нас и коэффициента прямоугольности петли гистерезиса исследуемого образца В ост/ В нас.
Размагнитьте образец, то есть уменьшите напряжение на автотрансформаторе (АТ) до нуля. При этом петля гистерезиса на экране осциллографа превращается почти в точку, соответствующую Н = 0 и В = 0.
Далее следует увеличивать напряжение на автотрансформаторе небольшими ступенями, и для каждой из них регистрировать напряжение на канале Х осциллографа - Ux и напряжение Uy на канале Y осциллографа. Теперь эти напряжения соответствуют не предельной петле гистерезиса (как в предыдущем упражнении), а частным петлям гистерезиса. Они несут информацию о точках на кривой намагничивания образца В(Н). Результаты измерений оформить в виде таблицы.
После окончания измерений образец размагнитить, то есть уменьшить переменный ток через обмотку N1 до минимального. Вычислите величины Н и В для каждой точки, а также относительную магнитную проницаемость
и построить график В(Н) и μ(Н).
Контрольные вопросы
1. Чем ферромагнетики отличаются от других веществ?
2. Привести примеры веществ, являющихся ферромагнетиками.
3. Почему магнитная индукция в ферромагнетиках, помещенных магнитное поле, значительно превышает индукцию этого поля?
4. Что такое домен? Почему ферромагнетик разбивается на домены?
5. Как происходит намагничивание ферромагнетиков?
6. Что такое петля гистерезиса? Какие причины ее вызывают?
7. В чем заключается осциллографический метод исследования?
8. Каким образом размагнитить ферромагнетик?
9. Что выражает относительная магнитная проницаемость?
10. Как определяется величина магнитной индукции образца при осциллографическом методе исследования?
Литература
1. А.Н. Матвеев.- Электричество и магнетизм: учеб. пособие для студентов вузов.- М: ОНИКС 21 век: Мир и образование, 2005. – 464 стр.
2. Калашников С.Г. Электричество.- M.: Физматлит, 2003.- 624 с.
3. Д.В.Сивухин. Общий курс физики. Т.III: Учеб. пособие.- М: Физматлит, 2004.- 656 с.
