Простой колебательный контур состоит из последовательно соединенных элементов: емкости С, индуктивности L и активного сопротивления R (рис. 1).
Если конденсатор зарядить, а затем замкнуть ключ К, то в контуре возникнут электромагнитные колебания. Действительно, при замыкании ключа К конденсатор С начинает разряжаться – в контуре появится нарастающий ток и пропорциональное ему магнитное поле. Изменение магнитного поля по закону электромагнитной индукции Фарадея приводит к возникновению в контуре ЭДС самоиндукции
, (1)
которая сначала (по правилу Ленца) замедляет скорость разрядки конденсатора, а после того как конденсатор полностью разрядится, начинает поддерживать ток в прежнем направлении. В результате происходит перезарядка конденсатора. Затем процесс разрядки начинается снова, но в обратном направлении, и т.д.
За время разрядки конденсатора энергия его электрического поля превращается в энергию магнитного поля в катушке индуктивности, и наоборот.
Максимальные значения напряжения на конденсаторе Um и тока Jm называются соответственно амплитудами 
колебаний напряжения и тока. Так как контур всегда обладает некоторым активным сопротивлением R, то часть энергии электромагнитных колебаний превращается в джоулево тепло, вследствие чего амплитуда колебаний в контуре постоянно уменьшается. С увеличением R затухание колебаний происходит быстрее, и, наконец, при достаточно большом R колебания вообще не возникают – наблюдается апериодический разряд конденсатора. Найдем уравнения, описывающие затухающие колебания в контуре. Допустим, что в момент замыкания ключа К (рис. 1.) обкладка 1 конденсатора была заряжена положительно. Тогда по закону Ома для неоднородного участка цепи
, (2)
где 
- разность потенциалов обкладок конденсатора, причем согласно сделанному выше допущению φ1 > φ2. По определению электроемкости:
, (3)
где q > 0 – заряд обкладки 1 конденсатора. Далее,
, (4)
поскольку заряд q на обкладке 1 конденсатора уменьшается. С учетом (3) и (4) уравнение (2) приводится к виду:
, (5)
где 
, 
- коэффициент затухания, 
. При β < ω0 уравнение (5) имеет следующее решение:
, (6)
где 
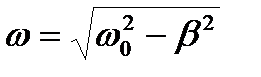. (7)
По определению, период затухающих колебаний вычисляется по формуле:
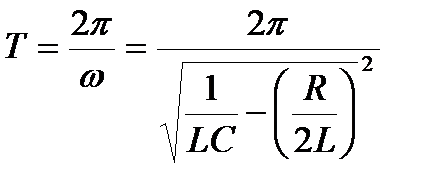. (8)
С увеличением коэффициента затухания β период колебаний растет, стремясь к бесконечности при 
. Это означает, что колебательный разряд переходит в апериодический процесс, когда 
. Для характеристики затухающих колебаний часто пользуются логарифмическим декрементом затухания
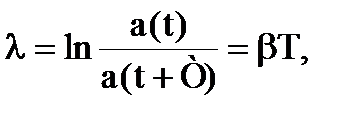(9)
где 
- амплитуда затухающих колебаний напряжения или тока.
В ряде случаев колебательный процесс можно исследовать, изучая зависимость U от J. Кривая, изображающая эту зависимость, называется фазовой кривой. Ток в контуре
(10)
Если β << ω, то 
, (11)
где 
.
Возводя уравнения (6) и (11) в квадрат и складывая, получим
.
В отсутствие затухания β = 0. Фазовая кривая имеет форму эллипса. При наличии затухания фазовая кривая представляет собой скручивающуюся спираль. Ее можно непосредственно наблюдать на экране осциллографа (рис. 2).
Исследование свободных затухающих колебаний проводится с помощью схемы, показанной на рис. 3.
Конденсатор с помощью реле автоматически подключается то к источнику постоянного напряжения (зарядка конденсатора), то к индуктивности L и сопротивлению R (разрядка конденсатора в контуре). Такое переключение происходит с частотой 50 Гц. Если включить генератор временной развертки осциллографа и синхронизировать его частоту с частотой переключения реле, то на экране осциллографа будет наблюдаться картина, изображенная на рис. 4.
Для получения фазовой кривой U(J), т.е. зависимости напряжения на конденсаторе от тока в контуре, достаточно включить генератор развертки осциллографа. При этом на вертикальный вход осциллографа будет по-прежнему подаваться напряжение с конденсатора, а на горизонтальный – с активного сопротивления. Так как на активном сопротивлении напряжение находится в фазе с током, то тем самым мы получаем зависимость напряжения U от тока в контуре (см. рис. 2).
