Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами.
Взаимодействие между покоящимися зарядами осуществляется через электрическое поле. Всякий заряд изменяет свойства окружающего пространства: создает в нем электрическое поле. Поле неподвижных зарядов не меняется со временем и называется электростатическим. Оно проявляет себя в том, что если в некоторую точку пространства поместить пробныйэлектрический заряд, то на него будет действовать сила. Пробным называется настолько малый точечный заряд, чтобы при его внесении в поле можно было пренебречь перераспределением заряда на телах, создающих поле.
Напряженностью электрического поля называют силу, действующую на единичный положительный пробный заряд:
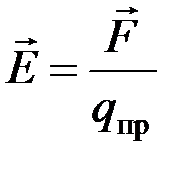. (1)
Если поле создано точечным зарядом q 0, то сила, действующая на пробный заряд q пр, определится из закона Кулона:
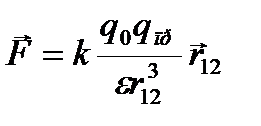, (2)
где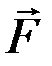 
– сила, действующая на заряд q пр со стороны заряда q 0, 
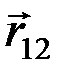– радиус–вектор, проведенный из точки 1, где находится заряд q 0 в точку 2, где находится заряд q пр, ε – относительная диэлектрическая проницаемость среды, в которой находятся заряды.
Коэффициент k зависит от выбора системы единиц измерения. В системе СИ единицей заряда является Кл (Кулон). Сила измеряется в ньютонах, расстояние в метрах. Для согласования единиц измерения с результатами опытов коэффициент k в системе СИ должен быть равен 9·10⁹ Н·м²/Кл². Этот коэффициент часто представляют в виде k = 1/4πε0, где ε0 = 8,85·10־¹² Ф/м, величина ε0 называется электрической постоянной.
Из соотношений (1) и (2) следует, что точечный заряд q 0 создает вокруг себя электрическое поле с напряженностью:
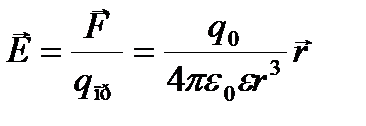, (3)
где r – радиус–вектор точки пространства, проведенный из точки, в которой находится заряд q 0, в точку наблюдения.
Если электрическое поле создается системой зарядов, то напряженность поля в данной точке наблюдения определяется по принципу суперпозиции:
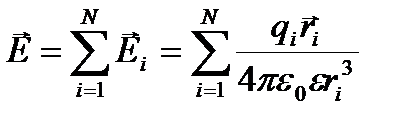, (4)
где qi – величина заряда с номером i, ri – радиус–вектор точки, в которой определяется напряженность, проведенный из той точки, где находится заряд qi.
Для наглядного изображения электрических полей пользуются методом силовых линий. Силовая линия есть математическая линия, направление касательной к которой в каждой точке совпадает с направлением вектора напряженности электрического поля в той же точке. Линии
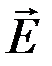точечного заряда представляют собой совокупность радиальных прямых, направленных от заряда, если он положителен, и к заряду, если он отрицателен. Линии одним концом опираются на заряд, другим уходят в бесконечность.
Работа сил электрического поля, созданного точечным зарядом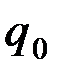 
, по перемещению заряда q из точки 1 в точку 2, вычисляется через криволинейный интеграл (все обозначения на рис. 1).
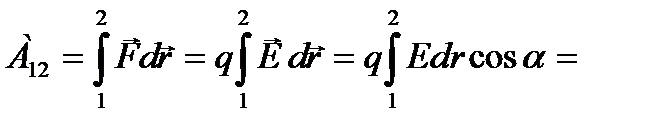
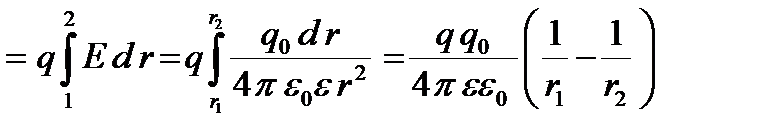(5)
Из формулы (5) следует, что работа сил электростатического поля по перемещению заряда из точки 1 в точку 2 не зависит от формы пути, а зависит лишь от положения начальной (1) и конечной (2) точки. Такое поле называется потенциальным.
Работу, совершаемую силами поля при перемещении единичного положительного заряда по произвольному пути из точки 1 в точку 2, называют разностью потенциалов:
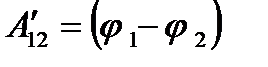. (6)
За единицу потенциала принимается такая разность потенциалов, при которой перемещение единицы заряда сопровождается работой, равной единице. В системе СИ это 1 вольт: 1В=1Дж/1Кл.
Разность потенциалов между точками 1 и 2 можно выразить через напряженность поля:
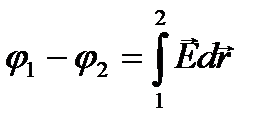. (7)
Напряженность поля можно определить, если известны значения потенциала в каждой точке пространства:
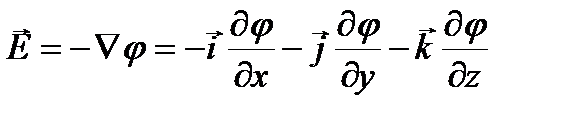. (8)
Векторная функция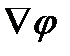 
скалярной величины 
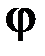называется её градиентом. Из соотношения (8) следует размерность напряженности электрического поля: в системе СИ единицей напряженности является 1 В/м.
Поверхность в пространстве, во всех точках которой потенциал имеет одно и то же значение, называется эквипотенциальной.
На рис. 2 оси Х и У являются касательными к эквипотенциальной поверхности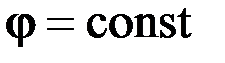 
. Значит в направлении осей Х и У потенциал не меняется, а следовательно производные 
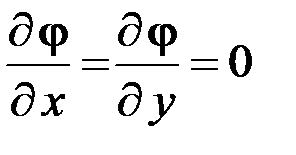. Ось Z направлена по нормали 
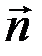к эквипотенциальной поверхности в сторону возрастания величины потенциала. Так как только производная 
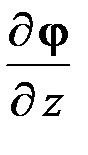отлична от нуля, то 
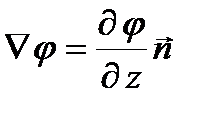, значит, функция 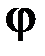наиболее быстро возрастает в направлении нормали 
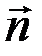к эквипотенциальной поверхности.
Поскольку вектор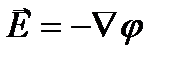 
, то он направлен в сторону наибольшего убывания потенциала. Силовые линии электростатического поля нормальны к эквипотенциальным поверхностям.
Разность потенциалов двух точек электрического поля называют напряжением и его измеряют, как и потенциал, в вольтах:
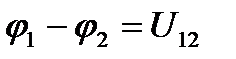. (9)
В однородном электрическом поле (например, между близко расположенными параллельными равномерно заряженными пластинами) силовые линии прямолинейны, параллельны и густота их везде одинакова, т.е.
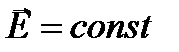и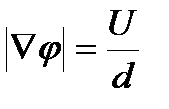 
, (10)
где d - расстояние между пластинами.
Формулы (8) и (10) широко используются для практических расчетов.
Метод исследования. В работе используется электрическое поле токов в электролите, потому что линии тока в электролите совпадают с линиями напряженности электрического поля. Это следует из закона Ома в дифференциальной форме:
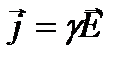, (11)
где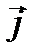 
- вектор плотности тока, γ – удельная электропроводность электролита.
Протекание постоянного тока через электролит сопровождается электролизом, вследствие чего поле токов может отличаться от электростатического поля. Чтобы исключить эффект электролиза, электростатическое поле моделируют полем переменных токов низкой частоты. Поскольку расстояние между электродами в ванне с электролитом мало, токи частотой 50 Гц можно считать
квазистационарными и структуру поля этих токов – аналогичной структуре электростатического поля.
Схема установки для измерения потенциала точек в электролитической ванне показана на рис. 3.
Электроды стоят на плоском горизонтальном дне ванны. В ванну налит тонкий ровный слой электролита (водопроводная вода) толщиной 1 см. Потенциал точек в электролите, а также потенциал электрода Э0 измеряются вольтметром с помощью зонда. Поле токов в плоскопараллельном слое электролита можно рассматривать как сечение соответствующего объемного электростатического поля. Силовые линии поля должны быть перпендикулярны к поверхности электродов, так как поверхность электродов можно считать эквипотенциальной, поскольку проводимость электрода значительно выше проводимости электролита. Поэтому в малом объеме элек тролита, прилегающем к электроду, электрическое поле можно считать однородным. Если на расстоянии d от электрода Э0, имеющего φ0 = 0, располагается эквипотенциальная поверхность потенциала φ1 (рис. 4), то напряженность поля Ех в выбранном объеме можно рассчитать по формуле (10). Примем малый объем в виде прямоугольного параллелепипеда, две грани которого совпадают с эквипотенциальными поверхностями φ0 и φ1 (рис. 4). В этом объеме силовые линии пересекают только грань с потенциалом φ1. Если ее площадь ΔS, то формула теоремы Гаусса будет иметь вид:
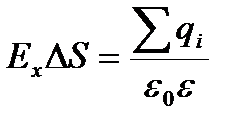. Отсюда плотность избыточного заряда на поверхности электрода:
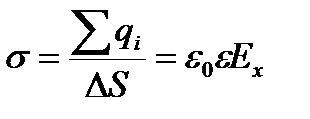(12)
Для воды при Т = 2830 К, ε = 80, ε0 = 8,85·10-12 Ф/м.
