Точность измерительных приборов ограничена, второстепенные связи влияют на результат измерений, поэтому при измерениях мы получаем не точное значение величины, а приближенное, содержащее неизвестную нам погрешность. Теория ошибок позволяет оценить предельные значения ошибки при измерении, т.е. определить интервал, в котором с заданной вероятностью находится истинное значение измеряемой величины.
Ошибки измерений делятся на:
1. Грубые ошибки (промахи), обусловленные неверными отсчетами, или неверными записями показаний приборов, грубой неточностью при настройке приборов, нарушением условий проведения опыта. На грубую ошибку отдельного измерения указывает резкое отличие его результата от предыдущих или последующих результатов. Результат измерения при грубой ошибке исключается.
2. Систематические погрешности, обусловленные причинами, одинаково действующими при всех измерениях, в частности, как результат неверных показаний приборов или неверного метода измерений, постоянного влияния внешнего фактора. Для устранения систематической погрешности используют методы измерений, основанные на сравнении величин, введении поправок в результаты измерений.
3. Случайные погрешности, обусловленные флуктуациями внешних и внутренних параметров при проведении измерений. Эти флуктуации случайны и заранее неизвестны. Случайные ошибки представляют собой ряд знакопеременных величин и присутствуют всегда при любых измерениях. Если при измерениях мы не обнаружили случайных ошибок, то это значит, что метод измерения недостаточно точен, либо приборы недостаточно чувствительны.
Теория ошибок определяет наиболее вероятное значение измеряемой величины как ее среднеарифметическое значение при измерениях одинаковой точности.
Основы теории случайных погрешностей разработаны немецким математиком К.Гауссом (1777-1855).
Гаусс установил закон нормального распределения, по которому распределяются ошибки данного ряда измерений. Закон Гаусса выводится исходя из следующих основных предположений.
1. Систематическая погрешность отсутствует.
2. Случайные погрешности могут иметь непрерывный ряд значений от -∞ до +∞
3. Случайные погрешности одинаковой величины, но разного знака, т.е. погрешности как в сторону увеличения, так в сторону уменьшения результата, встречаются одинаково часто.
4. Вероятность появления погрешности уменьшается с возрастанием величины погрешности, т.е., чем больше погрешность по абсолютной величине, тем реже она появляется.
5. Число измерений бесконечно велико (
)
При конечном числе измерений распределение дискретно. Закон нормального распределения показывает, что наиболее вероятны ошибки, близкие к нулю. Ошибки, равные по величине, но противоположные по знаку, равновероятны.
Кривые на рис.1 построены по закону нормального распределения (Гаусса) 
, что соответствует предельному значению бесконечно большого числа измерений, где σ - дисперсия измерений (см. ниже), (x - xi ) - случайная ошибка i -го измерения, x -истинное значение измеряемой величины.
Рис.1
Вероятность появления ошибки данной величины определяется выражением 
, где Δ n - число случаев появления ошибки данной величины, n - общее число случаев (измерений).
Наиболее вероятное значение измеряемой величины (модуль распределения) при нормальном распределении найдем как минимум суммы квадратов случайных ошибок:
. (1)
Из (1) следует, что наиболее вероятное значение измеряемой величины при измерениях одинаковой точности есть среднее арифметическое из всех результатов измерений:
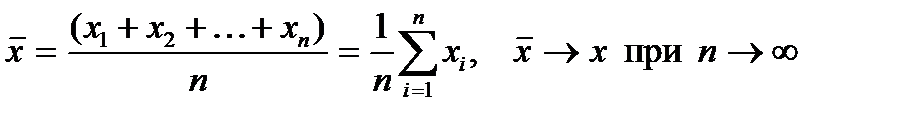, (2)
Погрешностью отдельного измерения называется разность между значением, полученным в данном измерении и средним арифметическим: 
.
Среднее арифметическое из абсолютных значений ошибок отдельных измерений называется абсолютной ошибкой измерения:
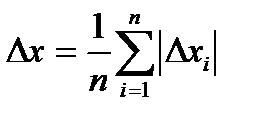, (3)
При большом числе измерений случайные ошибки равновероятны как в сторону превышения истинного значения величины, так и в сторону уменьшения, т.е. x заключено в интервале
. (4)
С увеличением числа измерений n средняя абсолютная погрешность уменьшается, следовательно, измерения следует производить столько раз, чтобы Δ х сравнялась с погрешностью прибора.
Относительной погрешностью измерений называется отношение средней абсолютной ошибки к среднему значению измеряемой величины, выраженное в процентах:
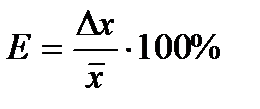. (5)
Относительная погрешность характеризует точность измерений. Величина случайной ошибки оценивается с помощью стандартной ошибки:
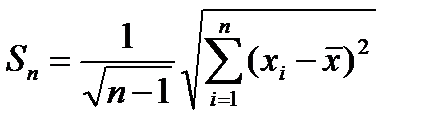. (6)
Статистический предел стандартной ошибки называется средней квадратичной ошибкой:
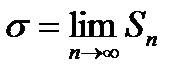(7)
Квадрат (7) σ2 называется дисперсией измерения.
Вероятность того, что результат i -го измерения xi отличается от истинного значения x на величину, не большую, чем абсолютная ошибка Δ х, равна
. (8)
Величина α называется доверительной вероятностью, а интервал значений от x -Δ х до x + Δ х называется доверительным интервалом.
Для характеристики величины случайной ошибки необходимо задать величину самой ошибки Δ х и величину доверительной вероятности α, что позволяет оценить степень надежности полученного результата.
Средней квадратичной ошибке Δ х = σ соответствует доверительная вероятность α = 0,68; при Δ х = 2σ – α = 0,95; при Δ х = 2σ – α = 0,997.
Среднее арифметическое 
отклоняется от истинного значения измерения x. На практике всегда проводится ограниченное число измерений, то есть из совокупности всех возможных значений случайной величины (генеральной совокупности) рассматривают случайную выборку конечного (небольшого) числа измерений (выборочную совокупность). При малом (n < 20) числе измерений распределение Гаусса переходит в распределение Стьюдента (Стьюдент – псевдоним английского математика и химика В.С. Госсета). При малом числе измерений количественную оценку разброса значений производят с помощью выборочной дисперсии.
Выборочная дисперсия отдельного результата измерений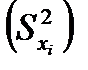 
равна:
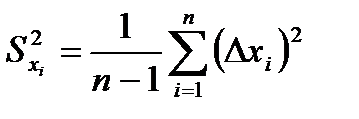. (9)
Корень квадратный из выборочной дисперсии называется средней квадратичной погрешностью отдельного измерения:
. (10)
Выборочная дисперсия среднего арифметического в n раз меньше выборочной дисперсии отдельного измерения:
. (11)
Отсюда следует 
, (12)
т.е. средняя квадратичная погрешность среднего арифметического в 
раз меньше средней квадратичной погрешности отдельного измерения. При малом числе измерений доверительный интервал выражается в виде:
(13)
где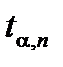 
- коэффициент Стьюдента, зависящий от доверительной вероятности α и числа измерений n. Значение коэффициента Стьюдента для различных значений α и n приведены в таблице 1.
Используя (13), равенство (8) можно записать в виде:
. (14)
Пример 1. Для выбранной доверительной вероятности α и заданного числа экспериментов n определяется из таблицы 1 коэффициент Стъюдента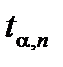 
: для α = 0,95 и n = 5 - t0,95;5 = 2,8; а для α = 0,95 и n = 3 - t0,95;3 = 4,3).
Таблица 1
