а) Найти закон распределения случайной величины Х:
6.1. Имеются четыре лампочки, каждая из них с вероятностью 0,2 имеет дефект. Лампочка ввинчивается в патрон, включается ток, при включении тока дефектная лампочка сразу перегорает, после чего она заменяется другой. Х - число лампочек, которое будет испробовано.
6.2. Составить закон распределения числа попаданий в цель при шести выстрелах, если вероятность попадания при одном выстреле равна 0,4.
6.3. Вероятность того, что студент найдет в библиотеке нужную ему книгу, равна 0,3. Составить закон распределения числа библиотек (Х), которые он посетит, если в городе четыре библиотеки.
6.4. На заводе работают четыре автоматические линии. Вероятность того, что в течение смены первая линия не потребует регулировки, равна 0,9; вторая - 0.8; третья - 0,75; четвертая - 0,7. Х - число линий, которые в течение смены не потребуют регулировки.
6.5. Х - число появлений события А в пяти независимых испытаниях, вероятность появления события А в каждом испытании равна 0,2.
6.6. Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Х - число промахов, если вероятность попадания в цель при одном выстреле равна 0,7.
6.7. Из партии в 25 изделий, среди которых 6 бракованных, выбирают для проверки три изделия. Х - число бракованных изделий в выборке.
6.8. Среди поступивших в ремонт 10 часов 6 нуждаются в общей чистке механизма. Часы не рассортированы. Мастер, желая найти часы, нуждающие-ся в общей чистке механизма, осматривает их подряд. Найдя такие часы, он прекращает осмотр. Х - количество проверенных часов.
6.9. Х - число появлений события А в трех независимых испытаниях, вероятность появления события А в каждом испытании равна 0,3.
6.10. В партии 10 % нестандартных деталей. Отобраны 4 детали. Х - число нестандартных деталей среди отобранных.
6.11. Производится два независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,75. Х - разность между числом попаданий и числом промахов.
6.12. Вероятность выпадения герба при каждом из пяти бросаний монеты равна 0.5. Составить закон распределения случайной величины Х - отношений числа выпадений герба к числу появлений решки.
6.13. Из 6 деталей, из которых 4 стандартных, отобраны три детали. Х - число стандартных деталей среди отобранных.
6.14. Два стрелка стреляют каждый по своей мишени. делая независимо друг от друга по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго - 0,7. Х - разность между числом попаданий первого стрелка и числом попаданий второго стрелка.
6.15. Х - число белых шаров среди трех выбранных наудачу из ящика, в котором 5 белых и 7 черных шаров.
6.16. На пути движения автомобиля 4 светофора. Каждый из них с вероят-ностью 0.5 либо разрешает, либо запрещает автомобилю дальнейшее движе-ние. Х - число светофоров, пройденных автомобилем до первой остановки.
6.17. Производятся три независимых испытания, при каждом из которых вероятность появления события А равна 0,4. Х - число появлений события А в указанных испытаниях.
6.18. Испытывается устройство, состоящее из трех независимо работа-ющих блоков. Вероятности отказа блоков таковы: р 1 = 0.3, р 2 = 0,5, р 3= 0,6. Х - число отказавших блоков.
6.19. Производится последовательные независимые испытания пяти приборов на надежность. Надежность каждого из пяти приборов равна 0,9. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Х - число испытанных в данном эксперименте приборов.
6.20. Из урны, содержащей 4 белых и 6 черных шаров, случайным образом и без возвращения извлекаются три шара. Х - число белых шаров в выборке.
6.21. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Х - число попаданий.
6.22. Из урны, содержащей 4 шара с номерами 1, 2, 3, 4, случайным образом достали два. Составить закон распределения случайной величины Х - суммы номеров шаров.
6.23. Рассматривается работа трех независимо функционирующих технических устройств. Вероятность работы первого - 0,2, второго - 0,4, третьего - 0,5. Х - число работающих технических устройств.
6.24. Бросаются три монеты. Х - число выпавших гербов.
6.25. Производится ряд независимых испытаний, при каждом из которых вероятность появления события А равна 0,6. Испытания проводятся до первого появления события А, после чего они прекращаются Х - число проведенных испытаний.
6.26. Приобретено 10 билетов, вероятность выигрыша равна 0,05. Х - число
лотерейных билетов, на которые выпадут выигрыши.
6.27. Рабочий обслуживает 4 станка. Вероятность того, что в течение часа первый станок не потребует регулировки, равна 0,9, второй - 0,8, третий - 0,75, четвертый - 0,7. Х - число станков, которые в течение часа не потребуют регулировки
6. 28. Х - число попаданий мячом в корзину при двух бросках, если веро-ятность попадания равна 0,4.
6.29. ОТК проверяет изделие на стандартность. Вероятность того. Что изделие стандартно 0,9. В каждой партии содержится 5 изделий. Х - число партий, в каждой из которой окажется 4 стандартных, если проверке подлежит 50 партий.
| Х | х 1 | х 2 | х 3 | х 4 |
| Р | р 1 | р 2 | р 3 | р 4 |
6.30. a)Производятся четыре независимых испытания элемента некоторого устройства, при каждом из которых вероятность отказа элемента равна 0,1. Х - число отказов элемента в четыре испытаниях.
б). Случайная величина Х задана рядом распределения.
1) Найти функцию распределения F (х) случайной величины Х и построить ее график. 2) Найти математическое ожидание М (Х) и дисперсию D (X) случайной величины Х, построить многоугольник распределения. Значения параметров х 1, х 2, х 3, х 4, р 1, р 2, р 3, р 4 вычислить по следующим формулам: R = остаток (N /4) + 2; N - номер варианта; х 1 = N +3, х 2 = х 1 + R, х 3 = х 2 + R; х 4 = х 3+ 2 R и р 1 = 1/(R + 5), р 2 = 1/(R + 3), р 4 = 1/(8 - R), р 3 = 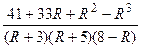 .
.
Задание 7а. Непрерывная случайная величина Х подчинена закону распределения с плотностью f (x). Требуется:1) найти коэффициент b; 2) найти интегральную функцию распределения F (x);3) построить графики функций f (x) и F (x); 4) найти математическое ожидание М (Х), дисперсию D (X) и s(Х) случайной величины Х и вероятность попадания CВ Х в интервал (х 1, х 2).
1. х 1= 0, х 2= 0,25

| 2. х 1 = 2, х 2=3
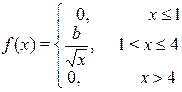
| 3. х 1 = 5p/6, х 2 =p
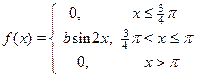
|
4. х 1 = 1, х 2 = 1,75
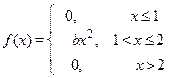
| 5. х 1 =0, х 2 = p/12
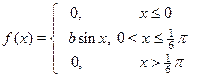
| 6. х 1 =1/27, х 2 =1/8

|
7. х 1 = 0, х 2=p/4
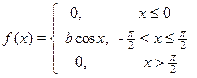
| 8. х 1= 1, х 2=2
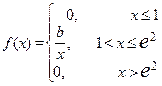
| 9. х 1 = 0, х 2 =1
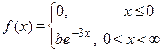
|
10 х 1 = 0, х 2 = 2
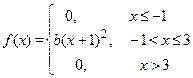
| 11 х 1 = 0, х 2 = 2
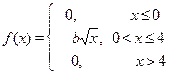
| 12 х 1 = 3, х 2 = 4

|
13. х 1 = -1, х 2= p/4
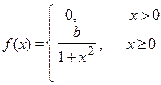
| 14. х 1 = 1, х 2=3
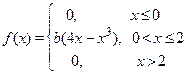
| 15. х 1 = p/4, х 2=p/2
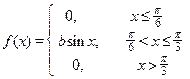
|
16. х 1 = 0, х 2 = 1,5

| 17. х 1 = 0,125, х 2 =8

| 18. х 1 = 0, х 2 = 0,5
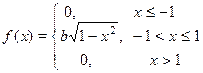
|
19. х 1 = –p/2, х 2= p/4,

| 20. х 1 = –p, х 2=0
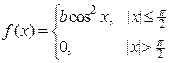
| 21. х 1 = –1, х 2 =1
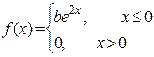
|
22. х 1 = 0, 5, х 2 = 1,5
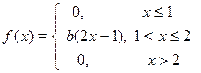
| 23. х 1 = 1, х 2=3

| 24. х 1 = 1, х 2 = 3 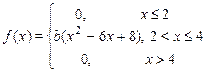
|
25. х 1 = –1, х 2 = p/4
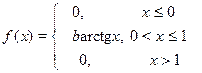
| 26. х 1 = 1, х 2 = 3
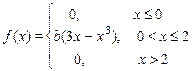
| 27. х 1 = p/2, х 2 = 3p/2

|
28. х 1 = -3, х 2 = -1
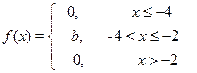
| 29. х 1 = 2, х 2=4
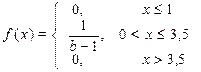
| 30. х 1 = p/4, х 2 = 3p/4
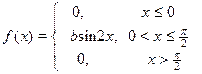
|
Задание 7б. Непрерывная случайная величина Х имеет функцию распределения F (x). Требуется:1) найти коэффициент а; 2) найти плотность распределения f (x); 3) построить графики f (x) и F (x); 4)найти вероятность попадания случайной величины Х в интервал (х 1, х 2).
1. х 1 = -p/4, х 2=0
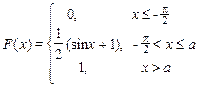
| 2. х 1 = 2, х 2=3
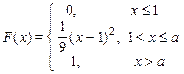
| 3. х 1 = 6, х 2=7
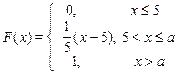
|
4. х 1 = p/4, х 2= p/3

| 5. х 1 = 1, х 2=1,5

| 6. х 1 = 1, х 2=1,25
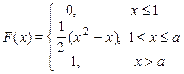
|
7. х 1 = p/2, х 2 = p

| 8. х 1 = 1,5, х 2=2,5

| 9. х 1 = –p/2, х 2 = p/2

|
10. х 1 = –p/2, х 2 = 0
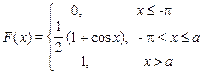
| 11. х 1 = 3, х 2 =4
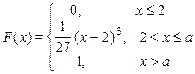
| 12. х 1 = 2, х 2 = 2,5
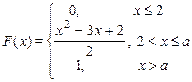
|
13. х 1 = 0, х 2 = p/2
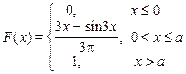
| 14. х 1 = 5, х 2 = 10

| 15. х 1 = 1, х 2=3
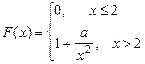
|
16. х 1 = 1, х 2 = 3
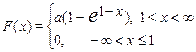
| 17. х 1 = –0,25, х 2 = 0,25
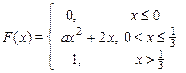
| 18. х 1 = 0, х 2= p/3
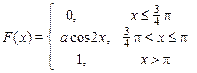
|
19. х 1 = 1,5, х 2 = 2.5
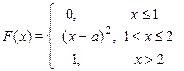
| 20. х 1 = p/12, х 2 = p/2
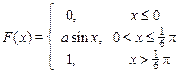
| 21. х 1 = p/4, х 2 = 3p/4
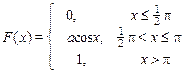
|
22. х 1 = 1, х 2 = 3

| 23. х 1 = 2, х 2 = 4
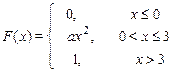
| 24. х 1 = 0, х 2 =1

|
25. х 1 = 2, х 2 = 4

| 26. х 1 = 0, х 2 = 0,5
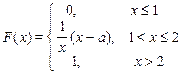
| 27. х 1 = –1, х 2 = 1
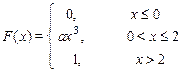
|
28. х 1 = 2, х 2 = 4
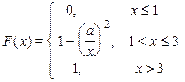
| 29. х 1 = –0,5, х 2 =0,5

| 30. х 1 = 0, х 2 = 2

|






