ИЗД Механика поступательного и вращательного движения. 17.1. Тело движется в плоскости ХОУ и при этом его координаты изменяются со временем следующим образом: х = 2 + 3t – t2

Вариант 17

17.1. Тело движется в плоскости ХОУ и при этом его координаты изменяются со временем следующим образом: х = 2 + 3 t – t ² , м и y = 4 – 2 t², м. Модуль ускорения этого тела в момент времени t = 2.0 c равен … м/с² (с округлением до десятых долей).

17.2. Тело массой m = 0,8 кг движется вверх по плоскости, наклоненной под углом α=30⁰ к горизонту. К телу прикреплена пружина жесткости k = 120 Н/м, к которой приложена сила (см. рисунок). Коэффициент трения между телом и плоскостью μ = 0,4. Ускорение тела равно а = 1,2 м/с². Определить деформацию пружины Δ l.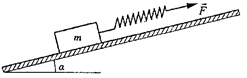

17.3. В потенциальном полесила пропорциональна градиенту потенциальной энергии . Если график зависимости потенциальной энергии от координаты х имеет вид, представленный на рисунке, то зависимость проекции силы на ось Х будет иметь вид …

17.4. Кусок пластилина массой m = 200 г падает со скоростью V = 6 м/с, направленной под углом α = 60⁰ к горизонту, на брусок массой m ₁ = 2 m, двигающийся со скоростью V ₁ = V /2 по гладкой горизонтальной поверхности навстречу куску пластилина. Найти количество энергии, перешедшей в тепло Q при абсолютно неупругом ударе.

17.5. Колесо автомашины вращается равноускоренно. Сделав N = 50 полных оборотов, оно изменило частоту вращения от n ₁ = 4 с^-1 до n ₂ = 6 с^-1. Определите угловое ускорение колеса.

17.6. Момент силы, приложенный к вращающемуся телу, изменяется по закону , где – некоторая положительная константа.

Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке …

17.7. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии 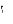друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили из состояния покоя до угловой скорости ₁, при этом была совершена работа А₁. Шарики раздвинули симметрично на расстояние 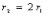и раскрутили до той же угловой скорости ₂ = ₁. Какая при этом была совершена работа?

1) ; 2) ; 3) ; 4) .

17.8. Обруч скатывается без проскальзывания с горки высотой h = 2,5 м. Найдите скорость обруча у основания горки при условии, что трением можно пренебречь.