Электрической цепи синусоидального тока

 

Цель работы:

1. Исследовать электрическое состояние линейной разветвленной цепи синусоидального тока при различных параметрах цепи.

2. Экспериментально проверить условие, при котором наблюдается резонанс токов. Определить добротность цепи.

3. Вычислить коэффициент мощности. При различных параметрах цепи определить активную, полную и реактивную мощности.

4. Построить по опытным данным векторные диаграммы напряжения и токов при различных режимах цепи: до резонанса, при резонансе и после резонанса.

 

Основные теоретические положения

 

Если к зажимам электрической цепи (рис.1), состоящей из параллельно соединенных катушки индуктивности (с активным сопротивлением R_к и индуктивностью L) и батареи конденсаторов (емкостью С), приложено напряжение, меняющееся во времени по синусоидальному закону u (t) = U_m sin wt, то токи в параллельных ветвях и неразветвленной части цепи также будут синусоидальными:

i_к (t) = 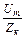sin (wt - j_к) = I_mк sin (wt - j_к);

i_с (t) = 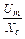sin (wt + j_c) = I_mc sin (wt + j_c);

i (t) = i _к (t) + i _с (t),

где X_с = - сопротивление батареи конденсаторов;

X_к = wL_к - индуктивное сопротивление катушки;

Z_к = 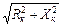- полное сопротивление катушки индуктивности;

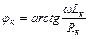; ; w = 2 pf;

f – частота синусоидального тока.

Рис. 1

По закону Ома в комплексной форме ток в катушке равен:

= = = =

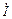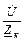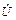
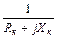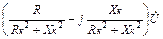= (g_к – j b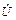_к) = Y _к = ,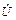

где Y _к = g_к – j b_к - комплекс полной проводимости катушки;

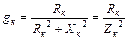- активная проводимость катушки;

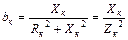- индуктивная проводимость катушки;

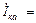g_к 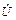- активная составляющая тока катушки, совпадающая по фазе с напряжением ;

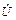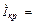– j b_к 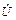- реактивная составляющая тока катушки, отстающая по фазе от напряжения 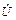на p /2.

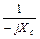
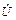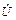Ток в ветви с конденсатором равен: = = jwС = jb_c .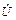

Ток в неразветвленной части цепи определяется формулой

=

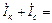
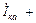
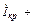
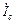
или 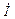= [ g_к – j (b_к – b_c)] 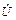= Y ,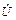

где Y = g_к – j (b_к – b_c) = ye^-jj = y cos j + jy sin j - комплекс полной проводимости всей цепи (рис.1);

j = arctg 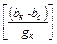- угол между напряжением U, приложенным ко всей цепи, и током в неразветвленной части цепи I;

y = 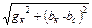- модуль полной проводимости цепи;

Векторная диаграмма токов (рис.2) строится на основании уравнения, составленного по первому закону Кирхгофа. Начальную фазу напряжения 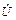принимают равной нулю, то есть 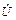= U, вектор напряжения 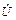совмещается с осью + I на комплексной плоскости.

На рис.2 приведена векторная диаграмма для случая, когда b_c > b_к (после резонанса) и напряжение 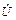отстает по фазе от тока 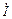на угол j < p /2. Ток в неразветвленной части цепи 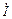носит активно-емкостной характер (I_c > I_кр).

 

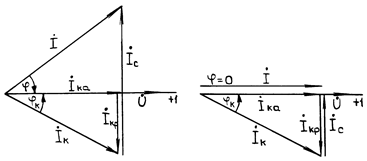
Рис.2 Рис.3

Резонансом тока называют явление в параллельной цепи с емкостными и индуктивными приемниками, когда общий ток в неразветвленной части цепи и напряжение на входе цепи совпадают по фазе. Резонанс токов характеризуется равенством реактивных токов в индуктивном и емкостном приемниках. Ток в неразветвленной части цепи минимальный, совпадает по фазе с напряжением и определяется активными составляющими токов емкостного и индуктивного приемников. Для цепи, представленной на рис.1, резонансное состояние характеризуется соотношениями:

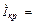
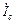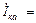
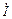, , j = 0.

Векторная диаграмма для резонансного режима представлена на рис.3.

 

 

Ток в неразветвленной части цепи определяется выражением

I = y U = U.

Поскольку при резонансе ток в неразветвленной части цепи чисто активный, то условием резонанса является равенство реактивных проводимостей приемников:

b_к = b_с или 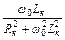+ w ₀² L_к ² = w ₀ C.

Это условие называется условием резонанса токов. Резонансное состояние можно получить, изменяя параметры цепи С, L_к, R_к или частоту напряжения сети w.

Резонансная частота f ₀ = w ₀ / 2 p определяется из условия резонанса

f ₀= .

Видно, что резонанс возможен лишь при условии 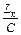>R_к. При резонансе ток в цепи I минимален: I = gU.

Реактивные токи в приемниках могут оказаться больше активного тока в неразветвленной части цепи. Превышение реактивных токов приемников при резонансе по сравнению с активным током в неразветвленной части цепи характеризуют добротностью цепи q.

q = .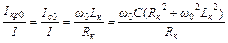

Мгновенная мощность в цепи есть произведение мгновенных значений тока и напряжения р (t) = u (t) i (t).

Активная мощность – среднее за период значение мгновенной мощности, то есть активная мощность характеризует среднюю мощность преобразования энергии в цепи в другие виды энергии:

P = 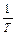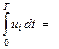UI cos j.

При параллельном соединении

P = UI_a = U ² g,

где U и I – соответственно действующие значения напряжения и тока в цепи;

j - угол сдвига по фазе между током и напряжением в цепи, зависит от характера нагрузки; g - активная проводимость цепи.

Полная мощность цепи – мощность, подводимая к зажимам цепи и характеризующая амплитуду колебаний мощности в цепи. Определяют полную мощность произведением действующих значений тока и напряжения

S = UI.

Реактивная мощность цепи – мощность, периодически запасаемая в реактивных элементах и отдаваемая ими обратно генератору, равная:

Q = UI sin j.

Комплексная форма полной мощности

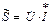= Scos j + jS sin j = P + jQ

дает возможность построить векторную диаграмму мощностей – треугольник мощностей (рис.4). Из векторной диаграммы мощностей находим полную мощность: S =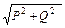

При резонансе реактивная мощность цепи Q = 0. Реактивные мощности на участках цепи с L_к и C характеризуют взаимное преобразование энергии электрического и магнитного полей индуктивности и емкости. Активная мощность P = S.

Резонанс токов используют в установках для повышения коэффициента мощности, подключая параллельно приемнику с сосредоточенными параметрами R, L конденсаторную батарею емкостью С:

C = I_c / 2 pfU = I_к sin j_к / 2 pfU,

Рис.4

которая обеспечивает полную компенсацию сдвига фаз между напряжением U и током I, при этом коэффициент мощности cos j = 1 и источник электрической энергии полностью разгружается от реактивного тока (S = P). Обычно коэффициент мощности установок доводят до 0,9…0,95. Еще большее повышение cos j требует больших затрат на установку батарей конденсаторов, которые экономически не оправдываются. В этом случае емкость батареи конденсаторов определяется формулой

C = (P / 2 pfU ²)(tg j_н - tg j),

где P - активная мощность приемника;

j_н - угол сдвига по фазе приемника;

j - требуемый угол сдвига по фазе.

Повышение коэффициента мощности установок снижает ток в линии электропередач, потери в линии DP_л = I ² R_л.

 

Описание установки

Экспериментальное исследование линейной разветвленной электрической цепи синусоидального тока выполняют на установке, схема которой приведена на рис.5. Цепь состоит из параллельно соединенных индуктивной катушки и конденсаторной батареи переменной емкости. Питание установки осуществляется от сети переменного тока 0 - А через двухполюсный выключатель В и регулирующий автотрансформатор ЛАТР, которым поддерживают на зажимах приемников заданную величину напряжения U, измеряемую вольтметром V. Ваттметр W измеряет активную мощность в цепи, а амперметры А, А ₁, А ₂ – токи I, I ₁ , I ₂ соответственно в неразветвленной части цепи и в отдельных ветвях.

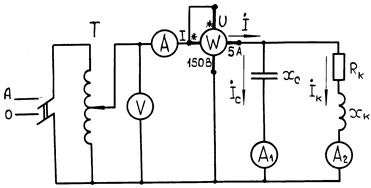
Рис.5

Порядок выполнения работы

1. Ознакомиться с приборами и оборудованием экспериментальной установки и записать технические характеристики в отчет.

2. Собрать схему, показанную на рис.5.

3. Поставить ручки регулирующего автотрансформатора ЛАТР в нулевое положение, выключить все конденсаторы в батарее и после проверки схемы руководителем замкнуть двухполюсный выключатель В.

4. Установить поворотом ручки регулирующего автотрансформатора заданную преподавателем величину напряжения U (80…100 В) на входе электрической цепи и на протяжении всего опыта поддерживать ее неизменной.

5. Изменяя емкость батареи конденсаторов, добиться резонанса в цепи: ток в неразветвленной части цепи достигнет минимального значения, активная мощность P = UI. Зафиксировать резонансную емкость.

6. Произвести опыты, изменяя емкость от 0 до C_p (3…5 опытов) и в таких же пределах выше C_p. Вблизи резонансной емкости измерения делать чаще. Данные измерений занести в табл. 1.

7. Результаты вычислений занести в табл. 1, 2. Учитывая, что параметры катушки индуктивности не изменялись, их достаточно вычислить один раз, например при резонансной емкости. При резонансе определить добротность цепи q.

8. По данным табл. 1 построить кривые I_c (C), I_к (C), I (C), cos j = f (C), j = f (C).

9. По опытным данным в масштабе построить три векторные диаграммы: до резонанса, в момент резонанса, после резонанса.

Указание: При построении векторной диаграммы нужно вспомнить, что I_к=I_L, только тогда, когда R_к » 0.

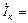
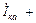
В нашем опыте R_к ¹ 0, поэтому 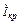, где I_ка и I_кр – активная и реактивная составляющие тока катушки; I_ка = g_кU; I_кр = b_кU или (см. рис.2): I_ка =I_к cos j_к; I_кр = I_к sin j_к = ; cos j_к = .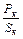

Так как активная мощность выделяется только на катушке, то показание ваттметра P и есть мощность катушки P_к.

Отсюда P = P_к = UI cos j = UI_к cos j_к = UI_ка = g_кU ² = R_кI _к ².

Построение векторной диаграммы токов и напряжений можно проводить так (рис.2):

1. Совместить вектор 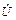с действительной осью;

2. Под углом j_к отложить вектор 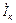= I_к e^-jjк;

3. От вектора 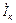провести вектор 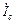, опережающий напряжение на угол p /2;

4. Замыкающий вектор = + .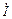

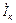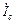При изменении емкости параметры катушки не изменяются, поэтому не изменяется ни величина, ни направление вектора 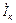, изменяется лишь по величине вектор .

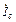Для исследуемой катушки известно: U, I_к, P_к= P.

По этим данным рассчитываются параметры катушки:

Z_к = U/ I_к, R_к = P/ I _к ², X_к = 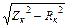, L_к = X_к / 2 pf, f = 50 Гц.

Для конденсатора известно U, I_c. Отсюда X_c = U/ I_c, b_c = I_c / U.

Таблица 1

№ Данные наблюдений

Результаты вычислений

С, мкФ

U, В

I, А

Iс, А

Iк, А

P, Вт

S, ВА

Q, ВАр

cosj

y, См -1

qк , Ом- 1

bк, Ом- 1

bc, Ом- 1

xc, Ом

q

1¸9

Таблица 2

C = Cp мкФ	Результаты вычислений
Zк	Rк	Xк	cos jк	Lк	gк

 

Вопросы для самоконтроля

1. Как определить полное сопротивление ветви электрической цепи синусоидального тока?

2. Какие величины определяют знак реактивного сопротивления ветви той же электрической цепи?

3. Как рассчитать ток в неразветвленной части электрической цепи синусоидального тока?

4. В какой электрической цепи и при каких условиях может возникнуть резонанс токов?

5. Чему равен коэффициент мощности цепи при резонансе токов?

6. Могут ли действующие токи в ветвях электрической цепи превышать действующий ток в неразветвленной части этой же цепи?

7. Какими величинами нужно располагать для расчета емкости конденсаторной батареи, обеспечивающей повышение коэффициента мощности установки до данного значения? До какого значения целесообразно повышать коэффициент мощности установок?

8. Чему равна реактивная мощность в цепи при резонансе токов?

Список литературы

1. Электротехника / Под ред. В. Г. Герасимова. – М.: Высшая школа, 1985. – С. 73-78, 81-88.

2. Касаткин А. С., Немцов М. В. Электротехника. – М.: Энергоатомиздат, 1983. – С. 63-98.

3. Иванов А. А. Электротехника: Лабораторные работы.- Киев: Вища школа, 1976. – С. 60-67.