Методы контурных токов и узловых потенциалов представляют собой универсальные средства расчета линейных электрических цепей. Однако в тех случаях, когда требуется найти ток только в одной ветви, применение этих методов может оказаться неоправданным из - за их громоздкости, так как матрицы сопротивления и проводимости несут много избыточной информации. А такие случаи встречаются довольно часто при анализе или расчете электронных схем. Здесь сказываются преимущества метода эквивалентного генератора. Он основан на теореме об активном двухполюснике или теореме Тевенина, которая формулируется следующим образом: произвольный линейный двухполюсник, содержащий источники (генераторы) напряжения и (или) тока, можно заменить активным двухполюсником, состоящим из одного источника (генератора) ЭДС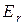 
и последовательно включенного внутреннего сопротивления 
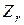. Значение 
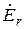числено совпадает с напряжением холостого хода 
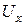исходного двухполюсника. Сопротивление 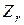равно входному сопротивлению двухполюсника при отсутствии источников, т. е. при замене источников ЭДС идеальными проводниками и разрыве тех ветвей, которые содержат источники тока.
Поясним применение этой теоремы для определения тока в цепи. Предположим, что в некоторой схеме (рисунок 2. 23, а) выделено две части: А- активная и П- пассивная. В активную часть, которую будем называть активным двухполюсником, входят источники энергии. В пассивной части, будем называть ее пассивным двухполюсником, источников энергии нет. Согласно теореме активный двухполюсник можно заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на его зажимах а - б, а внутреннее сопротивление –– его входному сопротивлению как пассивного двухполюсника.
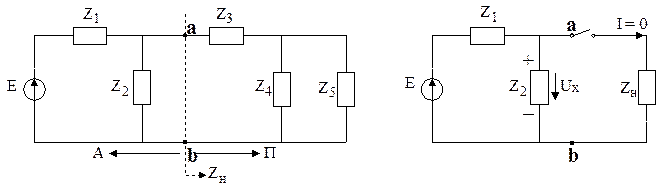
а) б)
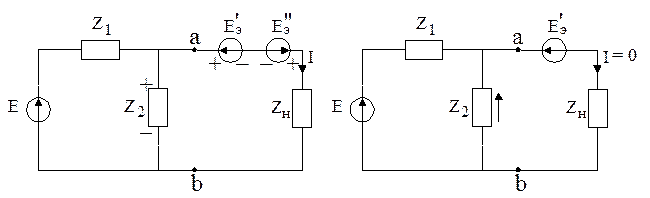
г) в)
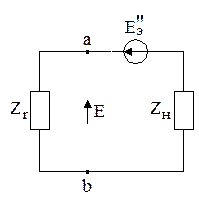
д)
Рисунок 2. 23
Разомкнем цепь между двухполюсниками, а пассивный двухполюсник П заменим его входным сопротивлением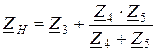 
. Ток в цепи становится равным нулю, а в месте разрыва (а, б) возникает напряжение холостого хода 
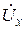(рисунок 2. 23, б). Введем между точками а, б ЭДС 
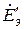, равную по величине 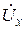, но противоположно ему направленную (рисунок 2. 23, в). Ток в цепи, соединяющей активный и пассивный двухполюсники, останется равным нулю, так как распределение потенциала в цепи не изменится. Введем между точками а, б еще одну ЭДС 
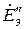, равную, но противоположную 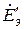(рисунок 2. 23, г). Очевидно, что эти две ЭДС скомпенсируют друг друга, и в цепи снова потечет ток 
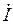. Применим к схеме рисунок 2.23, г принцип наложения: будем рассматривать ток как результат действия с одной стороны активного двухполюсника ЭДС 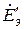(рисунок 2. 23, в), а с другой- ЭДС 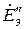(рисунок 2. 23, д). Во втором случае источники энергии из активного двухполюсника должны быть исключены, но оставлены их внутренние сопротивления. Левая схема рисунка 2. 22, в, точно такая же, как и схема рисунка 2. 22, б. Они отличаются лишь тем, что вместо разомкнутого ключа на рис. 2. 23, б, включена ЭДС, компенсирующую входное напряжение активного двухполюсника. В обоих случаях напряжение на сопротивлении нагрузки 
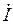и ток через него равны нулю. Искомый ток определяется схемой на рисунке 2. 22, д, и учитывая, что 
, запишем
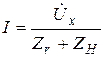. (2. 44)
Формула (2. 44) является математическим выражением теоремы об эквивалентном генераторе. ЭДС эквивалентного генератора, равную 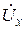, обозначают 
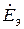или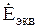 
, а его внутреннее сопротивление — 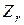, либо 
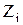. Параметры эквивалентного генератора находят с помощью уравнений Кирхгофа, методов контурных токов, наложения, узловых потенциалов.
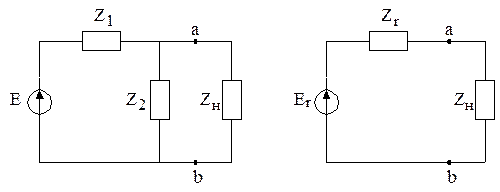
Пример. Заменить схему на рисунке 2. 24, а, по отношению к зажимам а, в эквивалентным генератором напряжения. Найдем вначале напряжение холостого хода на зажимах а, б: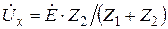 
.
а) б)
Рисунок 2. 24
Теперь найдем входное сопротивление схемы со стороны зажимов а, в, как пассивного двухполюсника (рисунок 2. 24, б):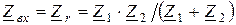 
.
Таким образом, параметры эквивалентного генератора:
.
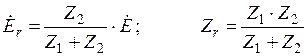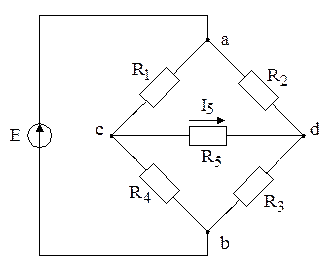
Пример. Методом эквивалентного генератора определить ток в ветви R5
(рисунок 2. 25, а)
а)
б) в)
Рисунок 2. 25
Разомкнем ветвь R5 (рисунок 2. 25, б) и найдем токи для режима холостого хода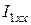 
и 
:
.
Определим напряжение холостого хода между точками с и d из уравнения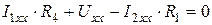 
, откуда 
.
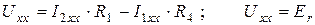Внутреннее сопротивление цепи (двухполюсника) относительно точек c d:
.
По принципу эквивалентного генератора схема цепи принимает вид рисунка 2. 25 в, где 
. Ток ветви R5 равен 
.
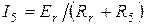2. 6. 4 Согласование в цепи переменного тока
|
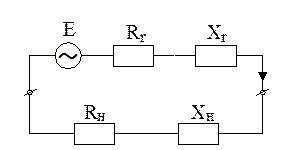
При совместной работе активного и пассивного двухполюсников в ряде случаев стремятся получить максимально возможную активную мощность, выделяемую в пассивном двухполюснике. Такой режим работы называют согласованным. Выясним условия, необходимые для режима согласования. Представим цепь в виде соединения генератора с внутренним сопротивлением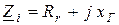 
и сопротивления нагрузки 
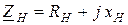(рисунок 2. 26). Комплексный ток в этой цепи определяется формулой (2. 44), где 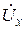заменим на :
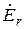или
.
Активная мощность, выделяемая в нагрузке, определяется формулой
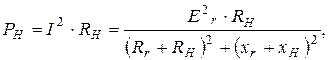Рисунок 2.25
где 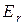— действующее значение ЭДС. Условимся считать сопротивление эквивалентного источника неизменным, а максимума мощности нагрузки будем добиваться путем изменения параметров нагрузки.
Прежде всего, как видно из формулы, частный максимум мощности можно достигнуть, если выбрать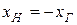 
. Тогда
.
Исследуя эту функцию на экстремум и считая переменной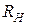 
, можно найти условие, при котором мощность будет максимально возможной: 
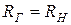. Окончательное условие согласования можно записать в виде:
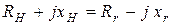. или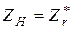 
(2.39)
что означает: для того, чтобы режим цепи был согласованным, комплексное сопротивление нагрузки должно быть комплексно сопряженным с сопротивлением источника. При этом мощность в нагрузке будет равна
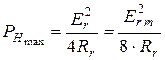. (2. 40)
Согласованный режим не всегда выгоден. Например, в цепях с большими мощностями более важным фактором является КПД. Нетрудно убедится, что в режиме согласования 
, т. е. КПД составляет 50%, что в ряде случаев недопустимо мало. В маломощных цепях, где КПД не имеет значения, согласование может быть полезным; так как позволяет получить максимальную мощность на нагрузке. В некоторых случаях согласование практически не выполнимо. Заметим, что свойства трансформатора преобразовывать сопротивление позволяют использовать его для согласования эквивалентного источника с нагрузкой.
Если сопротивления источника и сопротивления нагрузки чисто активны, то условие (2. 39) сводится к равенству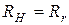 
.
Все рассмотренные методы расчета линейных цепей гармонического тока применимы также к цепям постоянного тока с той лишь разницей, что формально вместо комплексных сопротивлений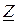 
или проводимостей 
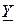нужно подставить сопротивление постоянному току R или проводимости G, а напряжения и токи считать постоянными. Конкретные расчеты цепей гармонического тока намного сложней расчета таких же по конфигурации цепей постоянного тока. так как связаны с операциями над комплексными числами.
