Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению данного участка цепи: 
.
Очевидно, что 
. Подставляя в эту формулу 
, получим
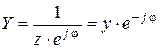, (2. 21)
где 
- полная проводимость участка цепи: 
.
Применяя к равенству (2. 21) формулу Эйлера, перепишем его в виде
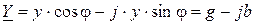, (2. 22)
где 
- активная проводимость;
- реактивная проводимость.
Используя алгебраическую запись комплексного сопротивления (2. 10), комплексную проводимость можно представить еще и так:
, (2. 23)
или
.
Сравнивая равенства (2. 22) и (2. 23), устанавливаем, что
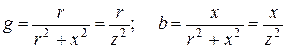. (2. 24)
Понятиями и величинами комплексной проводимости удобно пользоваться при параллельном соединении ветвей (рисунок 2. 9).
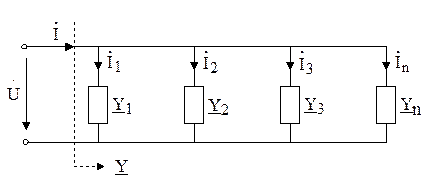
Рисунок 2. 9
Общий ток является суммой токов отдельных ветвей:
.
Величина 
является общей комплексной проводимостью цепи. Очевидно, что ее можно определить, суммируя активные и реактивные (с учетом знака) составляющие комплексных проводимостей ветвей.
Пример. Определить комплексную проводимость цепи, приведенной на рис. 2. 10. На основе формул (2. 24) находим
.
.
Следует заметить, что рассчитывать общий ток параллельного соединения через его общую проводимость имеет смысл, если это соединение входит как составная часть в более сложную цепь. Если же напряжение на зажимах параллельного соединения задано (идеальный источник напряжения), то токи в отдельных ветвях находятся по закону Ома, а общий ток- по первому закону Кирхгофа в комплексной форме.
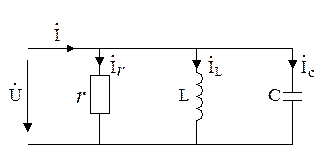
Рисунок 2. 10
Пример. Определить токи в цепи рисунке 2.10, если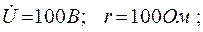 
. Находим комплексные токи в ветвях:
.
Общий комплексный ток найдем как сумму токов:
;
его модуль равен 
. Для наглядности определение тока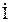 
показано на векторной диаграмме (рисунок 2. 11).
Рисунок 2. 11
Если в параллельном соединении имеется только две ветви, то его эквивалентное сопротивление проще определить не через проводимости, а используя непосредственно сопротивления:
откуда 
(2. 25)
Пример. Найти полное сопротивление цепи, изображенной на рис. 2. 12,
Рисунок 2. 12
если 
. Подставляя в формулу (2. 25) 
, находим
или 
; 
.
Заметим, что если бы элементы цепи имели одинаковый характер (оба резисторы или оба конденсаторы), то полное сопротивление равнялось бы 100 Ом.
