Метод наложения (его еще называют методом суперпозиции) заключается в том, что ток в каком-либо участке цепи определяют как результат независимого действия источников или групп источников. Метод наложения применим только к линейным цепям. Для понимания сущности метода наложения обратимся к выражению для контурного тока. Запишем, например, контурный ток 
схемы рисунке 2.21:
После подстановки вместо контурных ЭДС их выражений через ЭДС ветвей и приведения подобных членов, получим
.
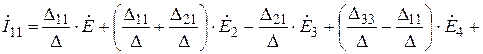
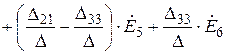Таким образом, контурный ток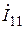 
, он же то ветви 
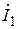, представляет собой линейную комбинацию произведений ЭДС ветвей на коэффициенты, имеющие размерность проводимости, что и является математическим выражением принципа наложения: ток (или напряжение) какого- либо участка цепи можно найти как алгебраическую сумму токов (напряжений), вызываемых в этом участке отдельными источниками или группами источников. Метод наложения применим, конечно, и к цепям, содержащим разнородные источники, т. е. источники напряжения и источники тока.
Пример. На рисунке 2. 22, а показана мостовая схема с источником ЭДС Е=0,5 В и источником тока J=1 мА. Сопротивления элементов имеют значения: R1=200 Oм; R2=300 Oм; R3=200 Oм; R4=300 Oм. Пользуясь принципом наложения определить токи во всех ветвях.
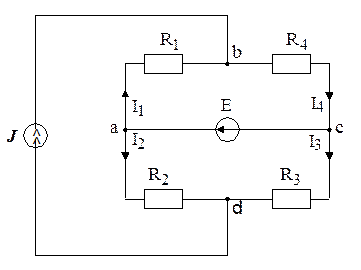
а)
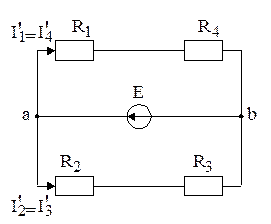
б)
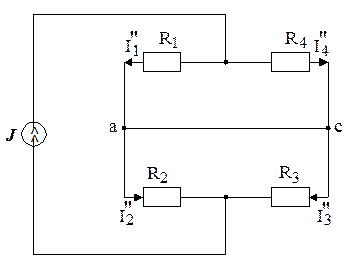
в)
Рисунок 2. 22
Решение. Для определения тока в ветвях с применением принципа наложения надо рассчитать токи в двух схемах, изображенных на рисунке 2. 22, б и в. В схеме на рисунке 2. 22, б J = 0 (точки b и d разомкнуты), а в схеме на рисунке 2. 22, в Е=0 (точки а и с соединены проводником без сопротивления). Токи в ветвях схемы (рисунок 2. 22, б):
.
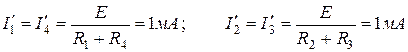Токи в ветвях схемы по рисунку 2. 20, в, где сопротивления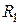 
и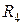 
, а также 
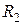и 
соединены параллельно:
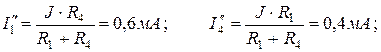
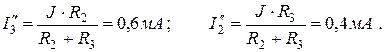
Токи в ветвях заданной схемы (рисунок 4. 20, а) равны алгебраическим суммам токов в соответствующих ветвях схем рисунка. 4. 20, б и в:
.
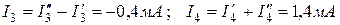Следует иметь в виду, что принцип наложения не применим к расчету мощностей, т. е. мощность, выделяемую в некотором сопротивлении нельзя вычислять как сумму мощностей, выделяемых в этом сопротивлении отдельными составляющими тока, так как мощность не является линейной функцией тока.
Пусть источник напряжения 
находится в ветви, принадлежащей контуру k, и создает некоторый ток в ветви, принадлежащей контуру j. Согласно выражению (2. 40), этот ток будет равен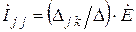 
. Если этот же источник поместить в ветви, относящиеся к контуру j, то в первой ветви возникает ток 
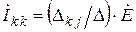. Так как для линейных цепей 
, то оба тока будут равны между собой. Рассмотренное свойство линейных цепей называется свойством или принципом взаимности.
