Так как треугольник PRQ «составлен» из прямоугольных треугольников RSP и PSQ, то из свойства 10.2 следует, . Теорема доказана

Теоремы Лежандра имеют большое значение при построении основ неевклидовой геометрии Лобачевского. В следующем параграфе они будут использованы нами при доказательстве утверждений, равносильных аксиоме параллельности евклидовой геометрии.

 

Теорема 11.1. Предположение о существовании треугольника, сумма углов которого совпадает с суммой двух прямых углов, равносильно аксиоме параллельности евклидовой плоскости.

Доказательство. В евклидовой геометрии, как следует из школьного курса математики, сумма углов любого треугольника на плоскости равна развернутому углу. Нас интересует обратное утверждение. Пусть на плоскости дан треугольник, сумма углов которого равна двум прямым углам. Докажем, что тогда справедливо утверждение: если даны точка и прямая, принадлежащие плоскости, причем точка не лежит на прямой, то существует единственная прямая, проходящая через данную точку и не пересекающая данную прямую.

Из второй теоремы Лежандра следует, что в условиях нашей теоремы сумма углов любого треугольника на плоскости равна 2d. Легко видеть, что это утверждение равносильно следующему свойству внешнего угла треугольника.

Лемма 11.2. Сумма углов треугольника равна 2d тогда и только тогда, когда его внешний угол равен сумме внутренних углов, с ним не смежных.

Доказательство. Необходимость. Пусть в треугольнике АВС (рис. 41). 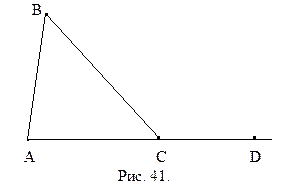Тогда . С другой стороны, внешний угол составляет с развернутый угол, поэтому . Отсюда следует, что .

Достаточность. Пусть . Так как , то . Отсюда следует, что . Лемма доказана.

Рассмотрим произвольную точку А и прямую m плоскости, точка А не принадлежит данной прямой. Опустим из точки А перпендикуляр АВ на прямую m (рис. 42) 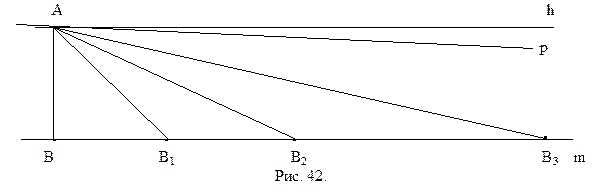и восставим в точке А перпендикуляр h к прямой АВ. Как известно, прямые m и h не пересекаются (теорема 4.2). Предположим, что через точку А проходит еще одна прямая р, отличная от h, не пересекающая m. Рассмотрим ту полуплоскость с границей АВ, в которой прямые p и h образуют острый угол. Отложим в этой полуплоскости на прямой m от точки В отрезок ВВ₁, равный АВ. Сумма углов треугольника АВВ₁ равна 2d. Угол АВВ₁ – прямой, поэтому . По построению - равнобедренный. Отсюда следует, что . Отложим на луче ВВ₁ от точки В₁ отрезок АВ₁. Получим точку В₂ (см. рис. 42). Угол АВ₁В треугольника АВ₁В является внешним углом . В силу нашего предположения, . А, так как треугольник АВ₁В₂ – равнобедренный, то 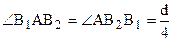. Следовательно, . Аналогично, откладывая на луче ВВ₁ от точки В₂ отрезок АВ₂, получим равнобедренный треугольник АВ₂В₃, угол В₂АВ₃ которого равен . Отсюда следует, что . Продолжая этот процесс, мы получим, что для любого n существует прямая ВАВ_n, лежащая внутри острого угла, образованного прямыми АВ и h, такая, что

.

При n стремящимся к бесконечности мы получим в правой части этого выражения бесконечно убывающую геометрическую прогрессию

,

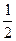первый член которой равен , а знаменатель - . Поэтому ее сумма S равна

.

Таким образом, . Поэтому существует такое натуральное число n, при котором будет больше угла, образованными прямыми АВ и р. Отсюда следует, что прямая р пересекает прямую m (см. теорему 7.7, § 7). Мы пришли к противоречию с нашим предположением. Теорема доказана.

Из доказанной теоремы легко проверить истинность следующего утверждения.

Теорема 11.3. Аксиома параллельности евклидовой геометрии равносильна утверждению: на плоскости существует выпуклый четырехугольник, сумма углов которого равна 4d.

Доказательство. В школьном курсе геометрии доказывается, что на евклидовой плоскости сумма углов выпуклого четырехугольника равна 4d. Докажем обратное утверждение. Пусть сумма углов выпуклого четырехугольника ABCD равна 4d (рис. 43). Проведем диагональ AD, получим два треугольника ABD и BCD. Легко видеть, что сумма углов этих треугольников совпадает с суммой углов данного четырехугольника. Предположим, что сумма углов треугольника ABD не равна 2d. Тогда по первой теореме Лежандра . Но из равенства суммы углов треугольников ABD и BCD и четырехугольника ABCD следует, что 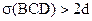, что в свою очередь противоречит первой теореме Лежандра. Таким образом, , и из теоремы 11.1 следует справедливость доказываемого утверждения.

Используя метод математической индукции, нетрудно также доказать следующее обобщение теоремы 11.3 на случай произвольного выпуклого n – угольника.

Теорема 11.4. Аксиома параллельности евклидовой геометрии равносильна утверждению: на плоскости существует выпуклый n - угольник, сумма углов которого равна 2(n-1)d..

Доказательство проведите самостоятельно.

Предложение Валлиса. На плоскости существует хотя бы одна пара треугольников с соответственно равными углами, но не равными сторонами.

Другими словами, на плоскости существуют два подобных, но неравных треугольника.

Теорема 11.5. Предложение Валлиса эквивалентно аксиоме параллельности евклидовой геометрии.

Доказательство. Из школьного курса геометрии известно, что на евклидовой плоскости существуют подобные, но не равные треугольники. Покажем обратное, если на плоскости даны два неравных треугольника с одинаковыми углами, то справедливо утверждение аксиомы параллельности евклидовой геометрии.

Пусть даны два треугольника АВС и А₁В₁С₁, такие, что

, (1)

и 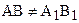. Будем для определенности считать, что

(2)

Воспользуемся аксиомой III₁ аксиоматики Гильберта евклидова пространства (см. § 4) и отложим от точки А на луче АВ отрезок АВ¢, равный А₁В₁. Используя аксиому III₄ аксиоматики Гильберта, отложим на луче В¢А угол , равный (рис. 44). Прямая h пересекла сторону АВ треугольника АВС в точке В¢, в соответствии с аксиомой II₄ (аксиома Паша, см. § 3) она пересекает вторую сторону этого треугольника. Предположим, что она пересекает прямую ВС в точке М (см. рис. 44 а). Тогда для треугольника В¢МВ угол 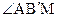- внешний и по построению он равен . Мы пришли к противоречию с теоремой 4.1 о внешнем угле треугольника. Таким образом, прямая h пересекает отрезок АС в некоторой точке С¢ (см. рис 44 б).

В силу условия (1) и равенства отрезков АВ¢ и А₁В₁, треугольники А₁В₁С₁ и АВ¢С¢ равны между собой по второму признаку равенства треугольников. Рассмотрим четырехугольник В¢С¢СВ. Очевидно, он является выпуклым. Из равенства треугольников А₁В₁С₁ и АВ¢С¢ следует, что углы этого четырехугольника удовлетворяют равенству:

.

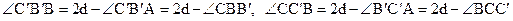Найдем сумму углов четырехугольника В¢С¢СВ:

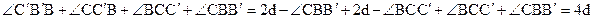
Мы построили выпуклый четырехугольник, сумма углов которого равна 4d, что, в силу теоремы 11.3, равносильно условию аксиомы параллельности евклидовой геометрии. Теорема доказана.

Следующее предложение, использованное Лежандром, носит его имя.

Предложение Лежандра. Перпендикуляр, проведенный к стороне острого угла в любой точке этой стороны, пересекает вторую сторону угла.

Теорема 11.6. Предложение Лежандра эквивалентно аксиоме параллельности евклидовой геометрии.

Доказательство. Предположим, что на евклидовой плоскости дан острый угол ВАС. Выберем произвольную точку м на луче АВ и восставим в этой точке перпендикуляр h к стороне АВ (рис. 45).

,

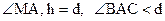поэтому прямые АС и h пересекаются в силу пятого постулате Евклида.

Обратно. Пусть на плоскости существует такой острый угол ВАС, для которого перпендикуляр, восставленный в любой точке стороны АВ, пересекает прямую АС. Выберем на стороне АВ этого угла точку М и восставим в ней перпендикуляр к АВ. В силу нашего предположения он пересекает сторону АС угла в некоторой точке N (рис. 46). Предположим, что дефект d треугольника AMN (см. определение 10.1) отличен от нуля. Тогда, в силу второй теоремы Лежандра, дефект любого треугольника PQR плоскости удовлетворяет неравенствам:

. (3)

Отразим симметрично точку А относительно точки М. Получим точку М₁. Восставим в точке М₁ перпендикуляр к прямой АВ. Он пересечет сторону АС данного угла в точке N₁ (см. рис. 46). В силу свойств центральной симметрии, . Из свойства 10.2 дефектов треугольников следует, что . Из свойства 10.3 следует, что . Отразим теперь точку симметрично относительно точки М₁, получим точку М₂. Восставим перпендикуляр к прямой АВ в точке М₂. В силу нашего предположения он пересечет сторону АС данного угла в некоторой точке N₂. Проведя те же рассуждения, получим, что . Отсюда следует, что . Отразим далее точку А относительно точки М₂, построим аналогичным образом треугольникAM₃N₃, затем треугольник AM₄N₄, и так далее. Получим треугольники AM₁N₁, 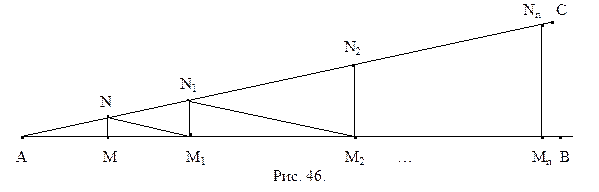AM₂N₂…AM_nN_n. Легко видеть, что . Выберем число n таким, чтобы выполнялось неравенство: 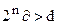. Поэтому . Мы пришли к противоречию с неравенством (3). Теорема доказана.

Следует заметить, что предложения, рассматриваемые Лежандром, их равносильность аксиоме параллельности евклидовой геометрии, были известны его предшественниками, в частности Саккери и Ламберту (см. §1). Лежандр, по сути, не внес ничего нового в решение проблемы пятого постулата Евклида. Но его учебники, в которых были опубликованы рассмотренные утверждения, оказали большое влияние на исследования Н.И. Лобачевского и Я. Бояи.

Определение 12.1. Четырехугольник, у которого два угла, имеющих общую сторону, являются прямыми, называется двупрямоугольником.

В двупрямоугольнике ABCD, у которого углы А и D прямые, стороны AD и BC называются соответственно нижним и верхним основаниями, а стороны АВ и СD – боковыми сторонами.

Определение 12.2. Если в двупрямоугольнике боковые стороны равны между собой, то он носит название четырехугольника Саккери.

Прежде всего, отметим следующее свойство двупрямоугольников.

Теорема 12.1. Двупрямоугольник ABCD в том и только в том случае является четырехугольником Саккери, когда его диагонали равны между собой.

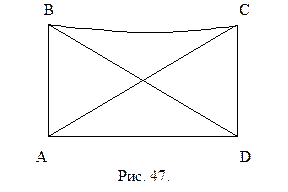Доказательство. Необходимость. Пусть ABCD – данный четырехугольник Саккери, углы А и D – прямые, боковые стороны АВ и СD равны между собой: (см. рис. 47). Треугольники ABD и ACD, в силу данных условий, прямоугольные. Они имеют общий катет AD, катеты АВ и СD равны между друг другу. Поэтому . Отсюда следует, что их гипотенузы АС и BD, которые служат диагоналями в данном четырехугольнике Саккери, также равны между собой. Необходимость доказана.

Достаточность. Рассмотрим двупрямоугольник ABCD, у которого углы А и D - прямые, а диагонали АС и BD – равны между собой (см. рис. 47). Тогда прямоугольные треугольники ABD и ACD имеют общий катет AD и равные гипотенузы АС и BD. Следовательно, они равны между собой по катету и гипотенузе. Отсюда следует, что их катеты АВ и CD также равны друг другу. Поэтому в двупрямоугольнике ABCD равны боковые стороны и он является четырехугольником Саккери. Теорема доказана.

Следующая теорема характеризует свойство углов четырехугольника Саккери, прилежащих к верхнему основанию.

Теорема 12.2. В четырехугольнике Саккери углы, прилежащие к верхнему основанию, равны между собой.

Доказательство. Пусть ABCD – четырехугольник Саккери (см. рис. 47). Тогда, в силу теоремы 12.1, его диагонали АС и BD равны между собой. Отсюда следует, что треугольники АВС и ВСD равны между собой по трем сторонам. Следовательно, . Теорема доказана.

Заметим еще раз, что доказанные теоремы основываются только на фактах абсолютной геометрии. Вернемся к результатам Омара Хаяма и Джироломо Саккери. Как упоминалось в первом параграфе, ими рассматривался четырехугольник Саккери и делались предположения о величине угла, прилежащего к верхнему основанию. Рассматривались случаи, когда этот угол тупой, прямой или острый (так называемые гипотезы тупого, прямого и острого углов). Гипотеза тупого угла была ими опровергнута, а Иоганн Генрих Ламберт (см. § 1) показал, что она реализуется на сфере трехмерного евклидова пространства. Было показано, что гипотеза прямого угла равносильна утверждению пятого постулата Евклида. Как Хаям, так и Саккери пытались найти противоречие между гипотезой острого угла и утверждениями абсолютной геометрии. Допущенные ошибки в рассуждениях позволили им сделать вывод, что проблема пятого постулата решена. На самом деле, гипотеза острого угла не может быть опровергнута средствами абсолютной геометрии. Она справедлива в пространстве Лобачевского, об этом мы будем говорить в следующей главе. Сейчас же мы рассмотрим гипотезы тупого и прямого углов.

Из первой теоремы Лежандра (теорема 10.1) легко следует, что углы, прилежащие к верхнему основанию четырехугольника Саккери, не могут быть тупыми. Для этого достаточно провести диагональ четырехугольника Саккери и рассмотреть суммы углов двух образовавшихся треугольников. Доказательство проведите самостоятельно в качестве упражнения. Покажем, что гипотеза прямого угла равносильна аксиоме параллельности евклидовой геометрии.

Теорема 12.3. Предположение о том, что углы, прилежащие к верхнему основанию четырехугольника Саккери равны прямым, равносильно аксиоме параллельности евклидовой геометрии.

Доказательство. Пусть дан четырехугольник Саккери АВСD, углы А и D которого прямые. Как известно, в евклидовой плоскости сумма углов выпуклого четырехугольника равна 4d. Таким образом, на евклидовой плоскости 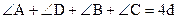. Так как , то . Из теоремы 12.2 следует, что 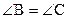. Поэтому углы В и С данного четырехугольника прямые.

Обратно, пусть существует такой четырехугольник Саккери АВСD с прямыми углами А и D, у которого по крайней мере один из углов, прилежащих к верхнему основанию, например, угол В, прямой. Тогда из теоремы 12.2 вытекает, что угол С также прямой. Поэтому сумма углов такого четырехугольника равна 4d. В силу теоремы 11.3 справедливо утверждение аксиомы параллельности евклидовой геометрии. Теорема доказана.

Следующее утверждение характеризует необходимое нам свойство двупрямоугольников.

Теорема 12.4. Пусть дан двупрямоугольник ABCD, у которого углы А и D прямые. Тогда боковая сторона АВ меньше боковой стороны CD, в том и только в том случае, когда .

Доказательство. Необходимость. Пусть ABCD двупрямоугольник, боковые стороны которого связаны неравенством (рис. 48). Требуется доказать, что . Отложим на боковой стороне DC от точи D отрезок DE, равный АВ. Тогда двупрямоугольник ABED – четырехугольник Саккери. Из теоремы 12.2 следует, что

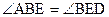. (1)

С другой стороны, Так как , то Е – внутренняя точка отрезка CD. Поэтому ВЕ – внутренний луч угла АВС. Следовательно,

. (2)

В треугольнике ВСЕ угол BED является внешним. По теореме о внешнем угле треугольника (теорема 4.1) этот угол больше любого внутреннего угла, с ним не смежного, т.е. . Отсюда, в силу соотношений (1) и (2) следует искомое неравенство.

Достаточность. Пусть дан двупрямоугольник ABCD, углы при верхнем основании которого подчиняются неравенству

. (3)

Следует доказать, что . Предположим, что его боковые стороны равны между собой. Тогда ABCD - четырехугольник Саккери. И, в силу теоремы 12.2, . Мы пришли к противоречию с данным нам условием (3). Поэтому боковые стороны АВ и CD не равны друг другу. Предположим, что . Но тогда из первой части доказательства нашей теоремы получим, что угол при верхнем основании, прилежащий к меньшей боковой стороне, т.е. больше угла, прилежащего к большей боковой стороне, т.е. . Мы опять пришли к противоречию с данным нам неравенством (3). Теорема доказана.

Доказанное свойство двупрямоугольников позволит нам усилить условие теоремы 12.2, получить признак, позволяющий утверждать, в каком случае двупрямоугольник является четырехугольником Саккери.

Теорема 12.5. Двупрямоугольник тогда и только тогда является четырехугольником Саккери, когда углы, прилежащие к верхнему основанию, равны между собой.

Доказательство. Необходимость следует из утверждения теоремы 12.3. Докажем достаточность. Пусть дан двупрямоугольник ABCD, у которого углы прилежащие к верхнему основанию равны между собой

(4)

Предположим, что боковые стороны АВ и CD не равны друг другу. Пусть, для определенности, . Тогда из теоремы 12.4 следует, что , что противоречит равенству (4). Теорема доказана.

Как отмечалось в § 1, одну из первых попыток доказательства пятого постулата Евклида предпринял Посидоний. Сформулируем его предложение в следующем виде.

Предложение Посидония. На плоскости существуют по крайней мере три коллинеарные точки, расположенные в одной полуплоскости от данной прямой и равноудаленные от нее.

Теорема 12.6. Предложение Посидония эквивалентно утверждению аксиомы параллельности евклидовой геометрии.

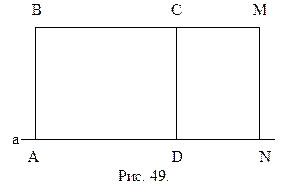Доказательство. На евклидовой плоскости, как следует из школьного курса геометрии, точки, расположенные на прямой, параллельной данной, равноудалены от нее. Перпендикуляры, опущенные из этих точек на данную прямую, равны между собой.

Докажем обратное. Предположим, что существует такая прямая а и такие три точки В, С и М, что перпендикуляры АВ, CD и MN, опущенные из них на прямую а, равны между собой (рис. 49). Тогда четырехугольники ABCD, DCMN и ABMN являются четырехугольниками Саккери. Предположим, что - острый. Тогда из теоремы 12.5 следует, что (т.к. ABCD – четырехугольник Саккери), (т.к. ABMN – четырехугольник Саккери), (т.к. DCMN – четырехугольник Саккери). Следовательно, . Из нашего предположения следует, что углы BCD и DCM острые. Но с другой стороны, они вместе составляют развернутый угол. Мы пришли к противоречию. Таким образом - прямой, а, следовательно, - также прямой. Четырехугольник ABCD имеет четыре прямых угла. В силу теоремы 11.3 выполнено условие аксиомы параллельности евклидовой геометрии. Теорема доказана.

Мы завершили исследование утверждений, эквивалентных аксиоме параллельности евклидовой геометрии. Следует отметить, что список рассмотренных нами утверждений не является полным. Существуют другие утверждения, также эквивалентные этой аксиоме. С некоторыми из них можно познакомиться в пособиях [7, 8, 9].

 

 

[1] Здесь и в дальнейшем прямой угол будем обозначать через d.