а)  ||
|| 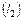
 ||
|| 
б) 

Пусть известны нормаль  к плоскости и направляющий вектор прямой
к плоскости и направляющий вектор прямой  , тогда
, тогда
а)  ||
|| 
 , (37)
, (37)
б)  ||
||  (38)
(38)
в)  (39)
(39)
Глава III. Элементы математического анализа
§ 1. Кванторы
 – «для любого
– «для любого  » – квантор всеобщности,
» – квантор всеобщности,
 – «существует
– «существует  такое, что …» – квантор существования,
такое, что …» – квантор существования,
 – «существует только одно
– «существует только одно  такое, что …» – квантор существования и единственности.
такое, что …» – квантор существования и единственности.
§ 2. Определение функций
Определение. Если каждому числу  поставлено в соответствие по некоторому правилу
поставлено в соответствие по некоторому правилу  вполне определенное действительное число
вполне определенное действительное число  , то говорят, что на множестве
, то говорят, что на множестве  определена числовая функция
определена числовая функция  , т.е.
, т.е. 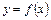 .
.
Множество  называют областью определения функции и обозначают
называют областью определения функции и обозначают  .
.
Определение. Если каждой паре  значений двух независимых друг от друга величин
значений двух независимых друг от друга величин  и
и  из некоторой области
из некоторой области  соответствует определенное значение величины
соответствует определенное значение величины  , то говорят, что
, то говорят, что  есть функция двух независимых переменных
есть функция двух независимых переменных  и
и  , определенная в области
, определенная в области  , т.е.
, т.е.

Область  при этом называется областью определения функции
при этом называется областью определения функции  .
.
При нахождении области определения функции двух переменных следует учитывать свойства элементарных функций.
| Функция | Область определения | ||
| 1. | 
| 
| |
| 2. | 
| 
| |
| 3. | 
| 
| |
| 4. | 
| 
| |
| 5. | 
| 
| |
| 6. | 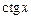
| 
| |
| 7. | 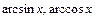
| 
| |
| 8. | 
| 
| |
§ 3. Предел функции 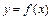 , непрерывность, точки разрыва
, непрерывность, точки разрыва
Рассмотрим
 – «
– « »–окрестность точки
»–окрестность точки  ,
,
 – выколотую «
– выколотую « »– окрестность точки
»– окрестность точки  .
.
Определение (по Коши): Число  называется пределом функции
называется пределом функции 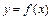 в точке
в точке  (или при
(или при  ), если для любого
), если для любого  существует такое число
существует такое число  , что для всех
, что для всех  , удовлетворяющих условию
, удовлетворяющих условию  выполняется неравенство:
выполняется неравенство:  .
.
 .
.

 – Первый замечательный предел
– Первый замечательный предел
 (40)
(40)
 – Второй замечательный предел
– Второй замечательный предел
Таблица эквивалентностей при 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
К неопределенностям относятся выражения вида  ,
,  ,
,  ,
, 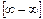 ,
,  и др.
и др.
1.  . Чтобы раскрыть неопределенность этого вида необходимо в числителе и знаменателе дроби выделить сомножитель, обращающий их в ноль и сократить на него дробь. Способы выделения сомножителя зависят от вида функции, например,
. Чтобы раскрыть неопределенность этого вида необходимо в числителе и знаменателе дроби выделить сомножитель, обращающий их в ноль и сократить на него дробь. Способы выделения сомножителя зависят от вида функции, например,
а) 
б) 

Можно также пользоваться таблицей эквивалентностей.
в) 

2.  . Чтобы раскрыть неопределенность вида
. Чтобы раскрыть неопределенность вида  можно пользоваться эквивалентными бесконечно большими, например,
можно пользоваться эквивалентными бесконечно большими, например,


3. Неопределенности вида  и
и 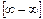 сводятся предварительно к неопределенностям вида
сводятся предварительно к неопределенностям вида  или
или  , например,
, например,
а) 

б) 



4. Неопределенность вида  раскрывается с помощью второго замечательного предела. Например,
раскрывается с помощью второго замечательного предела. Например,

 .
.
Определение. Функцию 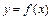 называют непрерывной в точке
называют непрерывной в точке  , если выполняются следующие три условия:
, если выполняются следующие три условия:
1)  определена в точке
определена в точке  , то есть
, то есть 
2) существует  ,
,
3) 
1. Если в точке  существуют конечные односторонние пределы и
существуют конечные односторонние пределы и  или
или  , то точку
, то точку  называют точкой разрыва I рода, устранимого.
называют точкой разрыва I рода, устранимого.
2. Если в точке  существуют конечные односторонние пределы и
существуют конечные односторонние пределы и  , то точку
, то точку  называют точкой разрыва I-го рода, неустранимого.
называют точкой разрыва I-го рода, неустранимого.
3. Если хотя бы один из односторонних пределов равен  или
или  , то точку
, то точку  называют точкой разрыва II рода.
называют точкой разрыва II рода.
Пример:

В точке  функция не определена, следовательно,
функция не определена, следовательно,  – точка разрыва.
– точка разрыва.
 ,
,

Следовательно,  точка разрыва II рода.
точка разрыва II рода.
§ 4. Производная функции одной переменной
Определение. Производной функции 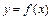 в точке
в точке  называют предел отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента
называют предел отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента  стремится к 0 (при условии, что этот предел существует)
стремится к 0 (при условии, что этот предел существует)

Геометрически производная определяет угловой коэффициент касательной к графику 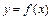 в точке
в точке  .
.
Уравнение касательной к кривой:
 , (41)
, (41)
уравнение нормали к кривой:
 , если
, если  (42)
(42)
Физический смысл:  характеризует мгновенную скорость изменения функции
характеризует мгновенную скорость изменения функции  при
при  .
.
Таблица производных
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
Правила дифференцирования
1. 
2. 
3. 
4. 
5. 
6. 
7. 

8. 
 (43)
(43)
9. 
 (44)
(44)
Правило Лопиталя
Теорема (Лопиталя). Если функции  и
и  :
:
1) дифференцируемы в некоторой окрестности точки  , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  ,
,
2) при  одновременно являются бесконечно малыми или бесконечно большими,
одновременно являются бесконечно малыми или бесконечно большими,
3)  в этой окрестности,
в этой окрестности,
4) существует предел отношения производных  (конечный или бесконечный), то существует и предел
(конечный или бесконечный), то существует и предел  , причем справедлива формула
, причем справедлива формула
 (45)
(45)
§ 5. План полного исследования функции:
I. Область определения и область непрерывности:
1) если есть точки разрыва, установить их характер, найдя пределы слева и справа;
2) выяснить, не является ли функция четной (график симметричен относительно  ) или нечетной (график симметричен относительно начала координат), периодической;
) или нечетной (график симметричен относительно начала координат), периодической;
3) точки пересечения с осями координат.
II. Асимптоты.
Прямая называется асимптотой кривой, если расстояние  от переменной точки
от переменной точки  кривой до этой прямой при удалении точки в бесконечность стремится к 0 (Точка удаляется в бесконечность, если ее расстояние от начала координат неограниченно увеличивается).
кривой до этой прямой при удалении точки в бесконечность стремится к 0 (Точка удаляется в бесконечность, если ее расстояние от начала координат неограниченно увеличивается).
Прямую  называют вертикальной асимптотой графика функции
называют вертикальной асимптотой графика функции 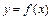 , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений  или
или  равно
равно  или
или  .
.
Прямую  называют наклонной асимптотой графика функции
называют наклонной асимптотой графика функции 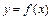 при
при  , если функцию
, если функцию  можно представить в виде:
можно представить в виде:
 где
где  при
при 
В этом случае
 ,
,  (46)
(46)
В частности, если функция  стремится к конечному пределу при
стремится к конечному пределу при  :
: 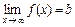 , то, очевидно,
, то, очевидно,  и линия
и линия 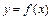 имеет горизонтальную асимптоту, параллельную оси
имеет горизонтальную асимптоту, параллельную оси  , именно
, именно  .
.
III. Точки экстремума, интервалы возрастания и убывания.
Теорема (Достаточный признак монотонности)
Если на некотором промежутке 
 имеет производную
имеет производную  для
для  , то на
, то на  функция возрастает
функция возрастает  (убывает
(убывает  ).
).
Теорема (Необходимое условие экстремума)
Если  дифференцируема в точке
дифференцируема в точке  и имеет в этой точке экстремум, то
и имеет в этой точке экстремум, то  .
.
Функция может иметь экстремум среди точек, в которых:
1)  ,
,
2)  ,
,
3)  – не существует, где
– не существует, где  .
.
Точки всех этих типов – критические точки функции.
Теорема (Достаточное условие экстремума)
Пусть  дифференцируема в
дифференцируема в  (кроме, быть может, самой точки
(кроме, быть может, самой точки  ). Если
). Если  – критическая точка
– критическая точка  и производная
и производная  при переходе через точку
при переходе через точку  меняет знак, то функция имеет в данной точке экстремум:
меняет знак, то функция имеет в данной точке экстремум:
максимум, если знак производной меняется с «+» на «–»,
минимум, если знак производной меняется с «–» на «+».
IV. Точки перегиба, интервалы выпуклости и вогнутости.
 Определение. Кривую
Определение. Кривую 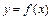 называют вогнутой в точке
называют вогнутой в точке  , если существует такая окрестность точки
, если существует такая окрестность точки  , в которой кривая расположена над касательной, проведенной к ней в точке
, в которой кривая расположена над касательной, проведенной к ней в точке  (рис. 5).
(рис. 5).
Определение. Кривую 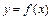 называют выпуклой в точке
называют выпуклой в точке  , если существует такая окрестность точки
, если существует такая окрестность точки  , в которой кривая расположена под касательной, проведенной к ней в точке
, в которой кривая расположена под касательной, проведенной к ней в точке  (рис. 6).
(рис. 6).
 |
Теорема (Достаточное условие выпуклости (вогнутости))
Если во всех точках  :
:  , то кривая
, то кривая 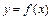 на этом интервале выпукла (вогнута).
на этом интервале выпукла (вогнута).
Определение. Точку, отделяющую выпуклую часть непрерывной кривой от вогнутой, называют точкой перегиба кривой.
Теорема (Достаточное условие перегиба)
Если  или не существует и при переходе через
или не существует и при переходе через 
 меняет знак, то точка кривой с абсциссой
меняет знак, то точка кривой с абсциссой  будет точкой перегиба.
будет точкой перегиба.
V. Построение графика.
§ 6. Частные производные функции нескольких переменных.
Производная сложной функции нескольких переменных
Определение. Частной производной функции  по переменной
по переменной  в точке
в точке 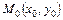 называется предел отношения частного приращения функции
называется предел отношения частного приращения функции  по
по  к приращению по
к приращению по  при неограниченном убывании последнего к нулю:
при неограниченном убывании последнего к нулю:

Другое обозначение:  .
.
Таким образом, частная производная функции  по переменной
по переменной  вычисляется в предположении, что значение
вычисляется в предположении, что значение  постоянно.
постоянно.
Аналогично:

Другое обозначение:  .
.
Частная производная функции  по переменной
по переменной  вычисляется в предположении, что значение
вычисляется в предположении, что значение  постоянно.
постоянно.
Частные производные функции  сами являются функциями этих же переменных и могут иметь производные, которые называются частными производными второго порядка.
сами являются функциями этих же переменных и могут иметь производные, которые называются частными производными второго порядка.



Пусть дана функция  , где
, где  ;
;  .
.
Тогда  ,
,
 . (см. рис. 7)
. (см. рис. 7)
 |
Если  , а
, а  ,
,  , то
, то
 (см. рис. 8)
(см. рис. 8)
 |
§ 7. Наибольшее и наименьшее значения функции
Наибольшее или наименьшее из всех значений нельзя смешивать с максимумом или минимумом функции, которые являются наибольшим или наименьшим значением функции только по сравнению с ее значениями в соседних точках.
Функция  , непрерывная в некоторой ограниченной замкнутой области
, непрерывная в некоторой ограниченной замкнутой области  , обязательно имеет в этой области наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри области
, обязательно имеет в этой области наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри области  , или в точках, лежащих на границе области.
, или в точках, лежащих на границе области.
Чтобы найти наибольшее или наименьшее значения функции  в ограниченной замкнутой области
в ограниченной замкнутой области  , где она непрерывна, можно руководствоваться следующим правилом:
, где она непрерывна, можно руководствоваться следующим правилом:
1. Найти критические точки, лежащие внутри области  и вычислить значения функции в этих точках.
и вычислить значения функции в этих точках.
2. Найти наибольшее или наименьшее значения функции на границе области  .
.
3. Сравнить полученные значения функции: самое большее из них и будет наибольшим, самое меньшее – наименьшим значением функции в области  .
.
§ 8. Неопределенный интеграл
Определение. Функция  называется первообразной функции
называется первообразной функции  на множестве
на множестве  , если для любого
, если для любого  выполняется равенство
выполняется равенство  .
.
Определение. Множество всех первообразных функций  для
для  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом  .
.
Т.е.

Таблица интегралов
-
 .
. -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 .
.
Метод замены переменной
Метод замены переменной состоит в том, что в интеграл  , нахождение которого затруднительно, вводят новую переменную
, нахождение которого затруднительно, вводят новую переменную  , связанную с переменной
, связанную с переменной  соотношением
соотношением
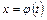 ,
,
где  – непрерывная монотонная функция, имеющая непрерывную производную
– непрерывная монотонная функция, имеющая непрерывную производную  на некотором интервале изменения
на некотором интервале изменения  .
.
Таким образом,

После того, как интеграл найден, возвращаются к первоначальной переменной с помощью подстановки  .
.
Пример:
 .
.
Метод интегрирования по частям
Интегрирования по частям основано на применении формулы
 (47)
(47)
Случаи применения формулы по частям.
I.  ;
;  ;
;  ;
;  .
.
II.  ;
;  ;
;  ;
;  ;
; 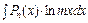 .
.
За  ,
,  ,
,
 ,
,
 ,
,
 ,
,
 .
.
III.  ,
,  .
.
Применяется двукратное интегрирование по частям.
Пример:
 .
.
Интегрирование рациональных функций
Найдем интегралы от простейших рациональных дробей:
1.  .
.
2. 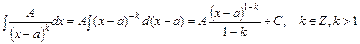 .
.
3.  ,
,
где 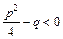 , т.е. квадратный трехчлен
, т.е. квадратный трехчлен  не имеет действительных корней.
не имеет действительных корней.
 .
.
Пример:



Интегрирование выражений, содержащих тригонометрические функции
1. Интегралы вида:  .
.
а) Если  и нечетное, то подстановка
и нечетное, то подстановка  приводит к интегралу от рациональной функции.
приводит к интегралу от рациональной функции.
Если  и нечетное, то к тому же приводит подстановка
и нечетное, то к тому же приводит подстановка  .
.
б) Если оба показателя  и
и  положительные и четные, то применяются формулы:
положительные и четные, то применяются формулы:
 (48)
(48)
в) Если оба показателя  и
и  отрицательные и сумма их четная, то подстановка
отрицательные и сумма их четная, то подстановка  приводит к интегралу от рациональной функции.
приводит к интегралу от рациональной функции.
При этом  ,
,  ,
,  .
.
2. Интегралы вида:

путем подстановки  сводится к интегралу от рациональной функции, при этом
сводится к интегралу от рациональной функции, при этом  .
.
3. Интегралы вида:Формулы:
 :
:  ,
,
 :
:  ,
,
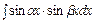 :
:  ,
,
Примеры:
1. 
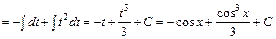 .
.
2. 
 .
.
3. 
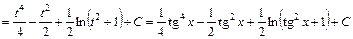 .
.
§ 9. Определенный интеграл
 Если
Если  на
на  , то определенный интеграл
, то определенный интеграл  представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями
представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями  (рис. 9).
(рис. 9).
Формула Ньютона-Лейбница:
 ,
,
где  – первообразная для
– первообразная для  .
.
Интегрирование по частям:
 , (49)
, (49)
где  – дифференцируемые функции на
– дифференцируемые функции на  .
.
Замена переменной:
 ,
,
где 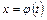 – функция непрерывная вместе со своей производной
– функция непрерывная вместе со своей производной  на отрезке
на отрезке  – функция непрерывная на
– функция непрерывная на  .
.
Если  – нечетная функция, то
– нечетная функция, то  .
.
Если  – четная функция, то
– четная функция, то  .
.
§ 10. Приложения определенных интегралов
1) Площадь криволинейной трапеции, ограниченной графиком функции 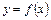
 , прямыми
, прямыми  и осью
и осью  вычисляется по формуле
вычисляется по формуле

2) Площадь плоской фигуры, ограниченной графиками функций
 и прямыми
и прямыми
 вычисляется по формуле:
вычисляется по формуле:
 (рис. 10) (50)
(рис. 10) (50)
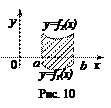 |
3) В полярных координатах площадь криволинейного сектора  , ограниченного кривой
, ограниченного кривой  и лучами
и лучами  вычисляется по формуле:
вычисляется по формуле:
 (рис. 11) (51)
(рис. 11) (51)
 |
4) Если тело образовано вращением вокруг оси  криволинейной трапеции, то его объем
криволинейной трапеции, то его объем
 (52)
(52)
5) При вращении вокруг оси  криволинейной трапеции, образуется тело вращения, объем которого
криволинейной трапеции, образуется тело вращения, объем которого
 (52')
(52')
6) Если плоская кривая  задана уравнением
задана уравнением  , то длина ее дуги от точки
, то длина ее дуги от точки  до точки
до точки  вычисляется по формуле:
вычисляется по формуле:
 (53)
(53)
Если  задана параметрически:
задана параметрически:
 , где
, где  , то длина ее дуги вычисляется по формуле:
, то длина ее дуги вычисляется по формуле:
 (54)
(54)
Если  задана в полярных координатах уравнением
задана в полярных координатах уравнением 
 , то длина ее дуги определяется по формуле:
, то длина ее дуги определяется по формуле:
 (55)
(55)
7) Работа переменной силы  , где
, где  – непрерывная функция на
– непрерывная функция на  , действующей в направлении оси
, действующей в направлении оси  на отрезке
на отрезке  вычисляется по формуле:
вычисляется по формуле:

8) Если материальная точка движется прямолинейно со скоростью  , то пройденный ею за промежуток времени от
, то пройденный ею за промежуток времени от  до
до  путь
путь  .
.
Глава IV. Пример решения варианта контрольной работы
Задача № 1. Вычислить определители  :
:
 .
.
Решение: По правилу вычисления определителя 2-го порядка:

По правилу треугольников:

Ответ:  .
.
Задача № 2. Решить систему  двумя способами
двумя способами
а) методом Гаусса;
б) по формулам Крамера, где  – матрица из задачи №1,
– матрица из задачи №1,

Решение:
Имеем:
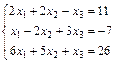
а) Переставим местами два первых уравнения

Составим расширенную матрицу системы

Первую строку умножим на «–2» и сложим со второй строкой.
Первую строку умножим на «–6» и сложим с третьей строкой.
Получаем матрицу:
 .
.
Переставим местами II и III уравнения:
 . Разделим II-ю строку на 17:
. Разделим II-ю строку на 17:
 .
.
Умножим II-ю строку на «–6» и сложим ее с III строкой:
 .
.
Этой матрице соответствует система уравнений:

б) по формулам Крамера: 
 .
.



Тогда: 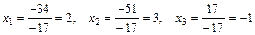 .
.
Ответ:  .
.
Задача № 3. Вычислить величину момента силы  , приложенной к точке
, приложенной к точке  относительно точки
относительно точки  , если
, если  .
.
 .
.
Решение:
Момент силы равен векторному произведению вектора  на вектор
на вектор  , т.е. по формуле (8) имеем:
, т.е. по формуле (8) имеем:

Так как
 имеем
имеем

Ответ:  .
.
Задача № 4. Даны координаты вершин пирамиды 
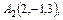

 .
.
Найти: а) площадь грани 
б) объем пирамиды.
Решение:
а) Воспользуемся формулой (10): 

Тогда площадь грани  равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах  и
и  , т.е.
, т.е. 
б) Воспользуемся формулой (11):

 .
.
Ответ:  ,
,  .
.
Задача № 5. Дано уравнение прямой. Записать его в следующих видах:
1. Уравнение в отрезках.
2. Уравнение с угловым коэффициентом.
Построить прямую в системе координат.
 .
.
Решение:
1.  По формуле (14):
По формуле (14):

2. По формуле (13):


Имеем  , т.е.
, т.е. 
Построим прямую  или
или 
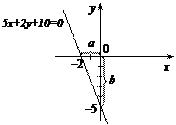
Ответ: 1. 
2. 
Задача № 6. Даны координаты вершин треугольника  . Найти:
. Найти:
1.
|
 Уравнение стороны
Уравнение стороны  .
.
2.
|
|
 .
.
3. 







|
|








