При параллельном соединении элементов (рисунок 1) уравнение по первому закону Кирхгофа для мгновенных значений и в комплексной форме имеет вид 
.
Рисунок 1
где 
, 
;
В зависимости от соотношения реактивных проводимостей 
и 
возможны три различных случая:
1. > , следовательно, 
> 
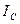Этому режиму соответствует векторная диаграмма на рисунке 2а.
2. = , ( = 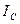) - случай резонанса токов (рисунок 2б).
3. < , а значит < 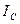. Этот случай иллюстрирует векторная диаграмма на рисунке 2с.
Рисунок 2
Из условия резонанса токов = можно определить резонансную частоту. Для схемы (рисунок 1) имеем
.
При этом 
.
Рисунок 3
На рисунке 3 показаны резонансные кривые параллельного контура. При резонансной частоте 
ток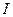 
от источника имеет минимум и равен току на активном сопротивлении 
, а ток на реактивном участке цепи равен нулю 
.
При 
цепь носит индуктивный характер (напряжение опережает ток на ток на угол 
), при - активный, а при 
- емкостной характер (ток опережает напряжение на угол ).
Полное сопротивление 
при резонансе принимает максимальное значение, а реактивное сопротивление 
обращается в ноль.
При определении резонансной частоты в общем случае следует исходить из условия вещественности полной проводимости цепи - 
. Например, для цепи (рисунок 4) имеем
Рисунок 4
Поскольку в режиме резонанса мнимая часть должна быть равна нулю, то
.