— Зачем же ты, бродяга, на базаре смущал народ, рассказывая про истину, о которой ты не имеешь представления? Что такое истина?
представление результатов измерений; прямые, косвенные, многократные измерения; нахождение зависимостей
1. ПРАВИЛА ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ
Результат измерений состоит из действительного значения и погрешности – при любых (прямых, косвенных, многократных) измерениях.
 действительное значение погрешность И
действительное значение погрешность И
 И= А+DА
И= А+DА
числа А и DА должны оканчиваться цифрами одинаковых разрядов;
DА – число с одним или двумя значащими цифрами (не более).
Например: U=12, 6 ± 1,2 - так надо U=12, 6 ± 1,2 345 - так нельзя
2. ПРИ ПРЯМЫХ ИЗМЕРЕНИЯХ
погрешность определяется классом точности прибора - если И произведено одним прибором (см. тему 2, «классы точности»)
Если измерительное устройство состоит из m СИ, каждый из которых имеет D i, суммарная погрешность абсолютная  относительная
относительная 
Щитовой амперметр с dА=1,5 %, подключенный через трансформатор тока с dТТ =1%, показывает 53А.

Показание представляется так: 53,0±0,8 А
3.ПРИ КОСВЕННЫХ ИЗМЕРЕНИЯХ
В общем случае. Для косвенного определения f = f (x,y,z) измерены х с погрешностью Dх, у с погрешностью Dу, z с погрешностью Dz.
Погрешность результата абсолютная

относительная

То есть, складываются погрешности, умноженные каждая на частную производную по той величине, которая измерена с этой погрешностью.
Например. Измерены U и I с погрешностями DU и DI, косвенно определяется мощность P=UI.

Результат: Р ± DР
Например.
Измерено напряжение U= 20 В с D= 2,5 В, ток I=10 A с D= 1,5А. Р=20×10 = 200 ВА.

Результат измерения: 200 ± 39 ВА
4. ПРИ МНОГОКРАТНЫХ ИЗМЕРЕНИЯХ
Определения.
Доверительный интервал – интервал, в котором с вероятностью Р находится истинное значение величины.
Доверительная вероятность – вероятность того, что истинное значение величины находится в доверительном интервале.
Для определения значения с заданной точностью (т.е. с заданной доверительной вероятностью или интервалом)
1. производят многократные измерения одной и той же величины, получают значения х 1, х 2, … х n. Они называются наблюдениями
2. определяют действительное значение как среднеарифметическое наблюдений

3. определяют абсолютные отклонения каждого наблюдения v i= x i -` x
4.находят среднеквадратическое отклонение (СКО) v i 
5.находят СКО действительного значения: 
6. задают доверительный интервал ks и получают доверительную вероятность Р,
либо наоборот - задают доверительную вероятность Р и получают доверительный интервал ks - в зависимости от цели измерения.
P и k при количестве наблюдений n<10 связаны распределением Стьюдента:
Фрагмент таблицы распределения Стьюдента
| n \ PÞ ß | 0,5 | 0,9 | 0,99 |
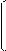 1,0 1,0
| 6,3 |  64 64
| |
| 0,82 | 3,9 | 10 k | |
| 0,77 | 2,4 |
Результат многократного измерения пишется: Хист = `х ± ks, Р.
Или х - ks < Хист<`х + ks, P.
Произносится:
« С вероятностью Р истинное значение величины лежит в интервале от `х - ks до `х + ks»
Например.
Напряжение измерено 4 раза, получены значения наблюдений 5.1, 5.2, 5.3, 5.4 В.
Действительное значение `U=(5.1+5.2+5.3+5.4)/4=5.25

Хочется знать доверительный интервал, например, с вероятностью 0,99.
Для Р =0,99 и n = 4 k = 6 (из распределения Стьюдента) Þ ks = 6•0,19=1,14
Результат измерения записывается так:
U = 5.25 ±1.14; Р = 0,99 Или 4.11< U <6.39, Р = 0,99.
Произносится: «истинное значение напряжения находится в интервале от 4.11 до 6.39 с вероятностью 0,99».
5.ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ МЕЖДУ ВЕЛИЧИНАМИ
Цель - с помощью измерений установить зависимость, связывающую функцию y с аргументом x, а именно:
1.график функции или
2.вид формулы (например, y=ax+b или y=ax2+bx+c или еще какой то) и значения постоянных в этой формуле (a, b, c).
Алгоритм определения зависимости в виде графика:
1. результаты измерений ввести в таблицу Excel;
2. выделить диапазон ячеек с данными для нанесения на диаграмму;
3.  на панели инструментов нажать кнопку;
на панели инструментов нажать кнопку;
4. выбрать опцию «график»,
5. выбрать вид графика из набора «стандартный» или «нестандартный» и нажать кнопку «далее»;
6. определить внешний вид названия, легенды и подписей, нажать кнопку «готово».
Алгоритм поиска зависимости в виде аналитическом
1. назначить формулу, описывающую искомую зависимость, из соображений:
а) физического правдоподобия, или б) удобства дальнейшего использования. Например:
y = a + bx + cx2 или y = abcx.
2. определить коэффициенты (a, b, c) такие, чтобы сумма квадратов отклонений была минимальной:
s2 = S (y - yi )2 = s2min
y - значение, полученное из формулы,
yi - значение, полученное измерением.
При изучении этой части курса следует обратиться к учебнику Метрологія та вимірювальна техніка. За редакцією проф. Є.С.Поліщука. Львів.-“Бескид Біт”.-2003.
Темы изложены на стр. 5¸119.
КЛАССИКА (избранное из учебников)






